Что такое классификация в машинном обучении?

Задача классификации на практике встречается гораздо чаще, чем регрессия. По счастливому совпадению, и решать ее в каком-то смысле гораздо проще. Формально, задача классификации состоит в предсказании какого-то дискретного значения, в противоположность регрессии - предсказанию непрерывного значения. Но в реальности задачи классификации очень непохожи на регрессионные. Задачи регрессии - часто экономические или статистические - состоят именно в прогнозировании некоторого уровня какой-то величины. Задача классификации (как, впрочем и следует из названия) сводится к отнесению конкретного объекта к одному из заранее известных классов. Вот эта “метка” - название класса - и выступает в роли целевой переменной. И, совершенно естественно, что классов может быть только конечное количество, поэтому целевая переменная - дискретная.

Важно, что классы должны быть заранее известны. Мы должны знать сколько их всего, и к какому классу относится каждый объект обучающей выборки. Если чего-то из этого мы не знаем, то это уже совершенно другая задача - кластеризация - которая относится к обучению без учителя. А для классификации в датасете должны быть приведены метки классов для каждого объекта. Иначе говорят, что датасет должен быть “размечен”. Если у нас этих данных нет, то данные надо разметить - указать для каждого объекта правильный класс.

Задачи классификации очень разнообразны. Почти любая прикладная задача машинного обучения может быть представлена в виде классификации. Например - распознавание объектов на изображении. Мы все пользуемся умными камерами в смартфонах, которые умеют автоматически определять, есть ли лицо на изображении в объективе. Вот там как раз работает алгоритм классификации, который разделяет все изображения на два класса - имеющих лицо и не имеющих. Другой пример - определение, является электронное письмо спамом или нет. Здесь так же идет разделение объектов на два класса. Или, например, выявление подозрительных банковских транзакций.

Все эти примеры имеют одну общую черту - в них идет речь о двух классах. Это примеры так называемой бинарной классификации. Такая постановка задачи действительно встречается довольно часто. И все эти задачи можно сформулировать как определение наличия или отсутствия какого-либо признака у объекта. Например, наличие лица на фото, подозрительности транзакции, и так далее. Но вообще не все задачи классификации обязаны быть бинарными. Иногда случается такое, что классов больше двух. Тогда мы говорим о задаче множественной классификации. Например, вместо распознавания конкретного объекта на изображении весьма распространена задача определения, какой именно объект изображен.

Это называется задача идентификации объекта. К задачам множественной классификации еще относятся, например, рубрикация текстов - определение тематики текста, классификация изображений, сегментация рынка, классификация товаров, и еще множество других. Более того, к задачам классификации относятся такие задачи, про которые вообще с первого взгляда непонятно, куда их относить и как их решать. Типичный пример - машинный перевод. При всей своей специфике, его тоже можно представить как задачу классификации - подбор следующего слова в тексте, соответствующего контексту и тексту на другом языке. Так как мы выбираем какое-то оптимальное значение из пусть большого, но не бесконечного количества значений - всех возможных слов языка. Так что перевод - это очень множественная, но все-таки классификация. То же можно сказать и о задаче генерации текста. Аналогично к классификации относится распознавание рукописных или сканированных текстов, преобразование речи в текст и многие другие задачи обработки естественных языков.

Кроме бинарной и множественной классификации еще выделяют одноклассовую и мультиклассовую. Одноклассовая - это когда один объект может принадлежать только одному классу. В мультиклассовой классификации каждый объект может принадлежать сразу нескольким классам. Например, текст может относиться сразу к нескольким темам. А на изображении может присутствовать сразу несколько объектов. Отдельно выделяют нечеткую классификацию - это когда объект может принадлежать некоторым классам с разной принадлежностью или вероятностью.

Еще следует отметить, что иногда имеет смысл преобразовать задачу регрессии в классификацию. Например, рассмотрим задачу предсказания цены финансового актива. Из-за того, что на цену актива влияют множество факторов, эта задача очень сложная, ведь мы выбираем из бесконечно большого количества вариантов. Но ее можно решать по-другому. Зачастую нам не важен конкретный уровень будущего значения цены, важнее то, будет цена больше или меньше, чем текущая. В таком случае, можно заменить сложную и зачастую нерешаемую задачу предсказания уровня более простой задачей предсказания тренда. У тренда можно выделить конечное число состояний - восходящий, нисходящий или боковой. То есть мы выбираем из, например, трех вариантов - будет цена больше, меньше или примерно такая же, как текущая. Другими словами мы заменили задачу регрессии классификацией. И такой прием используется очень часто.

Как определяется задача классификации?

Итак, рассмотрим математическую формализацию задачи классификации. В такой задаче, так же как и в регрессии, на вход модели подается вектор признаков $ x^{(i)} = (x_1, x_2, … x_n)$. Как и ранее, введем искусственный признак $ x_0 = 1 $. Он нужен для удобства представления многих моделей классификации. Можете представлять его как еще один столбец в датасете, в котором во всех строчках стоят единицы.

Функция гипотезы в таком случае будет иметь точно такой же вид: $ y = h_\theta (x) $. Существенное отличие в том, что целевая переменная $y$ будет принимать одно из конечного множества значений: $ y \in \lbrace y_1, y_2, …, y_k \rbrace $, где $k$ - это количество классов. Набор данных для можно представить как множество пар, состоящих из вектора признаков и значения целевой переменной.

Этот же набор данных иногда представляют как матрицу признаков (состоящую из векторов-строк для каждого объекта выборки) и вектора целевое переменной, также для каждого объекта выборки.

Сами метки классов в данных могут обозначаться как угодно, обычно текстом. В численных моделях гораздо удобнее представлять их в виде чисел. Но большинство реализаций моделей классификации прекрасно умеет работать и с нечисловыми метками классов. Поэтому условно, для удобства будем считать, что:

В дальнейшем для лучшего интуитивного понимания задач и алгоритмов классификации мы будем изображать объекты из датасета в виде точек на двумерном графике. А цвет или форма точек будут показывать, какому классу они относятся. Это хорошее визуальное представление. Но следует помнить, что на практике входной вектор может иметь сколько угодно измерений. То есть в датасете может быть сколько угодно признаков у каждого объекта. Тысячу или миллион признаков невозможно изобразить на графике, но это вполне может встретиться на практике.

Как мы уже говорили, классов тоже может быть произвольное количество. Но мы в начале будем рассматривать именно бинарную классификацию. Более сложные модели множественной или мультиклассовой классификации все равно строятся на основе бинарной. И на этих алгоритмах мы тоже остановимся. В такой формулировке мы будем предполагать, что $ y \in \lbrace 0, 1 \rbrace $, где 0 обычно принимается как «отрицательный класс» и 1 как «положительный класс», но вы можете назначить этим значениям любое представление. Как мы говорили, бинарная классификация - это часто про обнаружение какого-то признака у объекта, то есть положительный класс - это объекты, у которых этот признак присутствует, а отрицательный - это объекты, у которых этого признака нет. Хотя чисто математически, нет никакой разницы, как вы обозначите классы, это скорее общепринятое соглашение, которое облегчает понимание моделей и алгоритмов.

Логистическая регрессия

Одним из самых простых и распространенных алгоритмов классификации является логистическая регрессия. Пусть название «логистическая регрессия» не вводит в заблуждение. Метод назван таким образом по историческим причинам и на самом деле является подходом к проблемам классификации, а не регрессионным задачам. В следующих частях мы рассмотрим и принципиально другие модели классификации, но именно на примере логистической регрессии проще всего понять, как работает алгоритм классификации и какие общепринятые приемы и обозначения в ней используются. Логистическая регрессия это один из самых простых алгоритмов классификации, а что еще важнее - он очень похож и основан на уже известной нам модели линейной регрессии.

Перед рассмотрением сути метода логистической регрессии нужно задаться вопросом: почему мы не можем применить для классификации уже известные нам методы линейной регрессии? В самом деле, пусть модель предсказывает непрерывное значение, а мы будем его интерпретировать, как 0 или 1. Рассмотрим простой пример, в котором есть только один атрибут (отложен по горизонтальной оси), и на его основе мы хотим предсказать бинарное значение целевой переменной. Представим эти значения как 0 или 1 и отложим на вертикальной оси. Вот как может выглядеть датасет в таком виде:

Здесь явно наблюдается тенденция, что в имеющихся данных у положительных объектов значения атрибута выше, чем у отрицательных. Конечно, это такие идеализированные, искусственные данные, но на этом примере мы попытаемся понять главный принцип классификации. На этих данных вполне можно обучить модель парной линейной регрессии. Именно на этом датасете она может выглядеть примерно так:

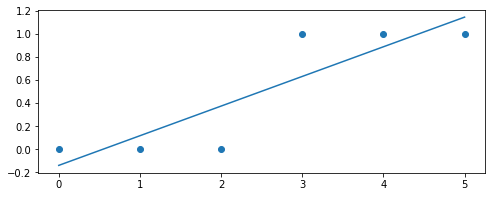
Но так как нам надо предсказывать точно либо 0, либо 1, придется ввести специальное пороговое значение. Например, если модель выдает значение больше 0.5, мы предсказываем положительный класс, если меньше - то отрицательный. Это вполне нормальный способ перевести непрерывное значение в дискретное, многие реальные модели классификации этим приемом успешно пользуются. Но в этом подходе заключается проблема. Регрессионные модели по сути своей неограничены и их значение может возрастать или убывать сколько угодно. Как это может быть проблемой? Давайте предположим, что в наших данных появилась еще одна точка:

Эта новая точка никак не изменяет общую картину, она прекрасно вписывается в уже имеющееся распределение данных, ничему не противоречит. Эта точка только подтверждает общую тенденцию, что у положительных объектов более высокий уровень факторной переменной. Но давайте посмотрим, что эта новая точка сделает с нашей моделью. Если мы изобразим предыдущую линию регрессии с учетом этой новой точки то получим следующую картину:

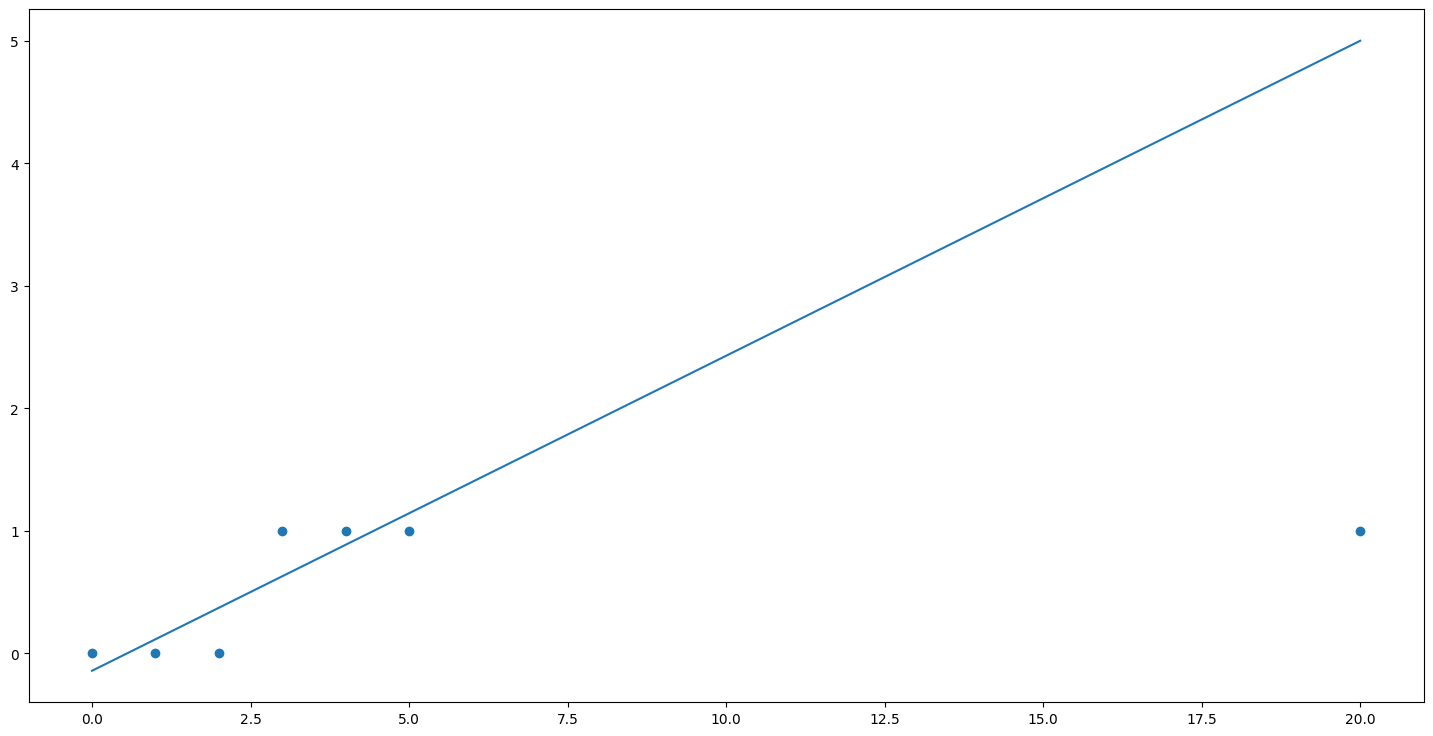
Эта модель даст огромную ошибку в появившейся новой точке. Поэтому если мы обучим регрессионную модель заново, то алгоритм обучения регрессии вынужденно сместит линию модели вниз, вот так:

Получается, что линия регрессии очень чувствительна к расположению точек, которые никак не влияют на общую тенденцию и принцип классификации. Но из-за этих расположений старое значение порога, которое мы выбрали, ориентируясь на предыдущую модель, уже не будет разделять классы правильно. То есть нам каждый раз придется вручную подбирать значение этого самого порога.

Это очень неудобно и ненадежно. И происходит потому, что регрессионные функции как правило неограничены. Но в принципе идея использовать регрессию здравая. Надо только преобразовать нашу функцию таким образом, чтобы вместо области значений $ y \in (-\inf, \inf) $ она имела, скажем, $ y \in (0, 1) $.Это можно легко сделать, используя нелинейное преобразование. Например, так:

В этой формуле $ z = X \cdot \vec{b}$, то есть обычная линейная комбинация значений факторов и параметров. По сути, это и есть результат работы модели линейной регрессии, но теперь эта линейная комбинация передается в нелинейное преобразование, которое ограничивает область значений и сверху и снизу. За счет этого, значение функции гипотезы будет ограничено и асимптотически приближаться к 1 при неограниченном увеличении $z$ и приближаться к 0 при неограниченном уменьшении $z$. При использовании такого преобразования график функции гипотезы будет выглядеть так:

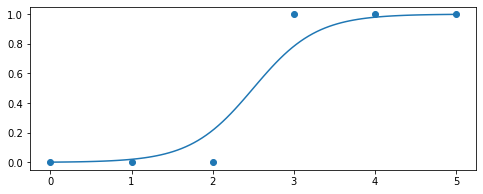
Сама эта нелинейная функция называется логистической или сигмоидной функцией. Именно из-за ее применения вся модель называется логистической регрессией. В принципе, можно использовать и другие нелинейные функции, которые имеют ограниченную область значений, например, арктангенс. Но на практике логистическая функция используется гораздо чаще, потому что она проще и работать с ней дальше гораздо удобнее. Не забывайте, что для машинного обучения мало определить саму функцию гипотезы, надо еще составить алгоритм обучения, то есть подбора параметров. Об этом и поговорим дальше.

В такой формулировке значение функции гипотезы $h_\theta (x)$ всегда будет лежать в диапазоне от 0 до 1. Поэтому это значение может быть проинтерпретировано как вероятность того, что данный объект принадлежит к положительному классу. Например, $h_\theta (x) = 0.7$ дает нам вероятность 70%, что класс данного объекта - положительный. Другими словами,

Вероятность того, что наше предсказание равно 0, то есть класс данного объекта - отрицательный, является просто дополнением вероятности того, что класс положительных (например, если вероятность положительного равна 70%, то вероятность отрицательного класса равна 30%).

Для практического использования логистической регрессии для классификации также необходимо выбрать значение порога. По умолчанию он берется равным 0,5. Принципиальное отличие от использования обычной линейной функции в том, что значение порога не будет так сильно зависеть от конкретного расположения точек. И поэтому не нужно каждый раз вручную подбирать его значение после каждого обучения модели. Логистическая регрессия устроена таким образом, что значение порога 0,5 всегда в среднем дает неплохие результаты классификации, и поэтому его можно использовать, не анализируя конкретное распределение точек выборки.

Граница принятия решений

Вернемся к пороговому значению функции гипотезы, ведь оно играет в понимании и интерпретации модели логистической регрессии. Чтобы получить дискретную классификацию, то есть конкретное значение целевой переменной 0 или 1, мы можем перевести непрерывное значение функции гипотезы, используя тот самый порог (по умолчанию, 0,5), следующим образом:

Логистическая функция $g$ ведет себя таким образом, что когда ее вход равен нулю, ее выход равен 0,5. Если входное значение больше нуля, то значение логистической функции будет больше, и наоборот. Напомним, что на вход ей подается линейная комбинация атрибутов и признаков, то есть значение линейной регрессии. Следует запомнить особые случаи значений логистической функции:

Таким образом, область пространства признаков, где $z = 0$ формирует границу между областью, точки которой модель относит к положительному классу и областью, точки которой модель относит к отрицательному. Граница принятия решения - это множество точек пространства параметров (то есть векторного пространства $b$), которая разделяет область, где y = 0 и где y = 1. Она создается нашей функцией гипотезы.

Граница принятия решения существует в любой модели классификации, не только в логистической регрессии. Это граница, которая отделяет область точек, классифицируемых как один определенный класс. Граница принятия решения есть и в моделях множественной классификации. Вообще, форма и сложность границы принятия решения - это одна из основных характеристик моделей машинного обучения для классификаций. Если возможно изобразить границу принятия решения графически, это всегда дает очень полное представление о работе модели. К сожалению, это можно сделать только в очень маломерных случаях, либо при использовании специальных методов, типа алгоритмов понижения размерности.

В нашем примере с классификацей по одной переменной граница принятия решения представляет собой точку - такое значение $x$, что логистическая функция в этой точке принимает значение ровно 0,5. Положение этой точки на оси $x$ задается следующим уравнением:

А что будет происходить в случае, когда входных переменных две - $x_1$ и $x_2$? Пространство признаком уже будет представлять собой плоскость. А значение сигмоиды будет поверхностью над этой плоскостью:

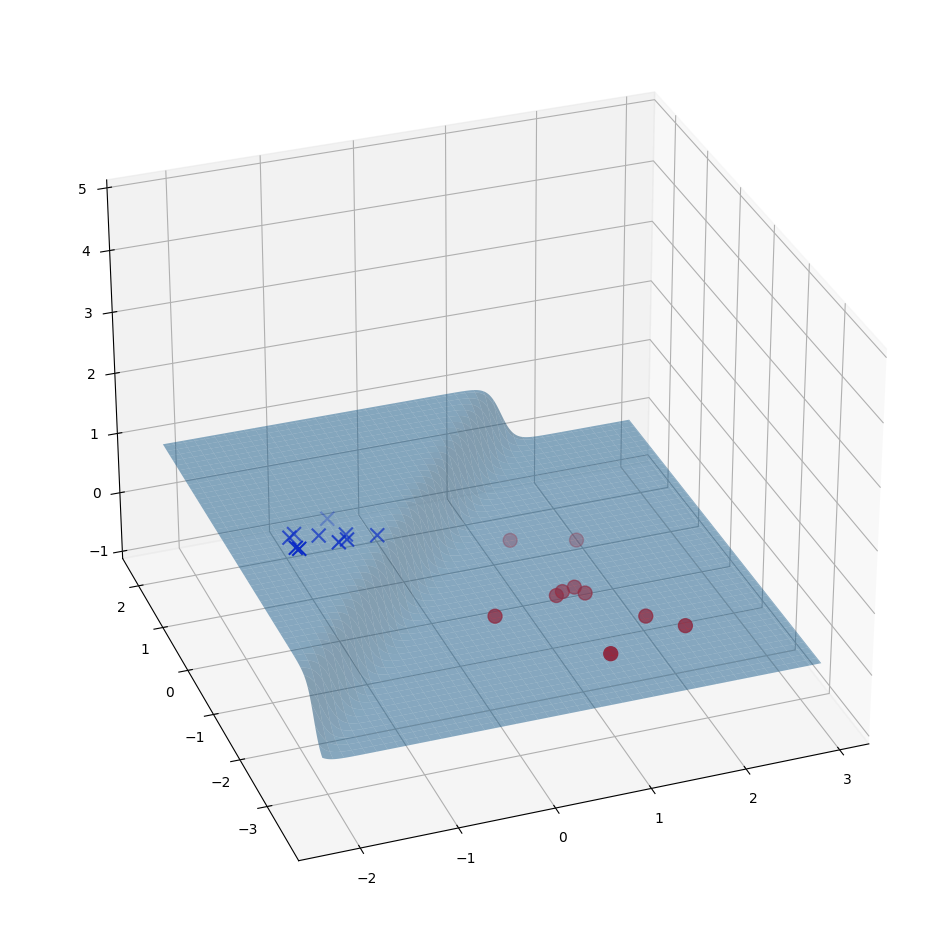
Соответствующая линейная функция будет плоскостью:

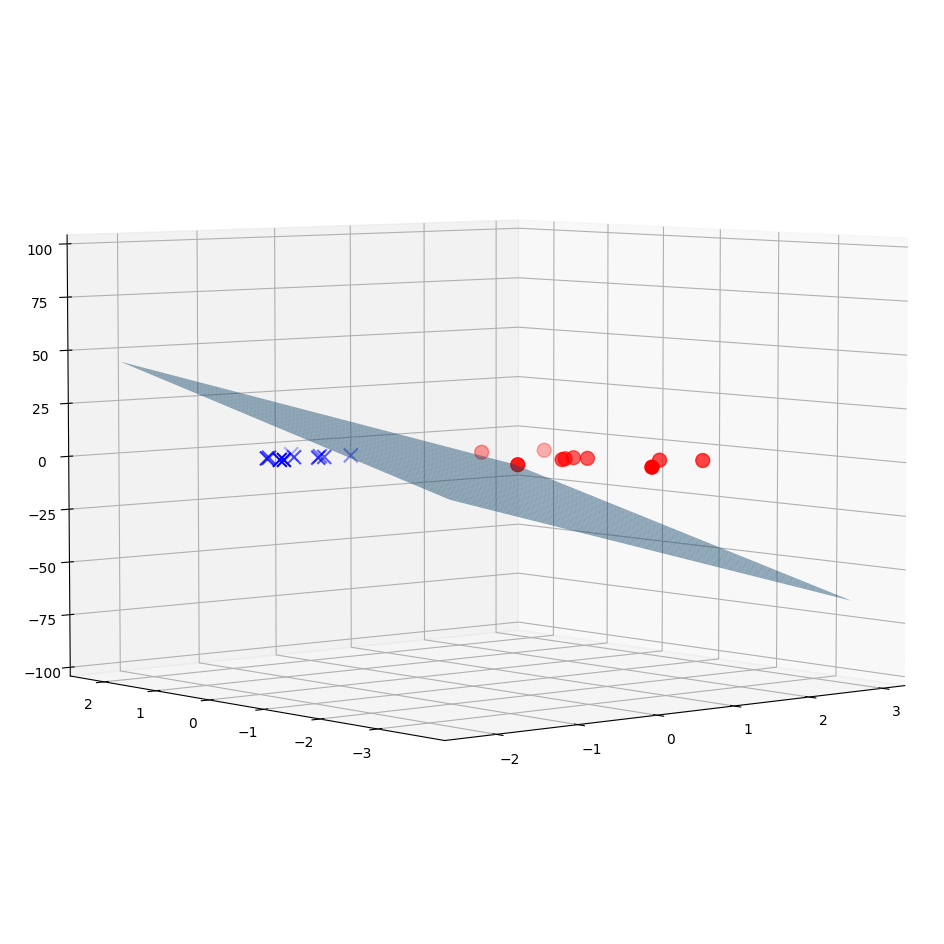
В таком случае, граница принятия решения будет задаваться таким уравнением:

Форма границы принятия решения полностью определяется видом модели, который мы применяем. В данном случае мы имеем линейную функцию. Поэтому граница тоже может быть только линейной. Если бы мы взяли другую функцию, например, полином второй степени, то граница принятия решения была бы поверхностью второго порядка. Именно поэтому логистическая регрессия считается именно линейной моделью. Несмотря на то, что в ней используется нелинейное преобразование, граница принятия решения в этой модели всегда линейна.

А вот конкретное положение границы принятия решения зависит от значений параметров модели. И именно это мы и подбираем в ходе машинного обучения. Поэтому процесс обучения модели классификации можно представить как процесс нахождения оптимальной границы принятия решения. Отсюда, кстати, следует основное ограничение метода логистической регрессии. Она будет показывать хорошие результаты тогда, когда объекты нашей выборки могут быть разделены гиперплоскостью.

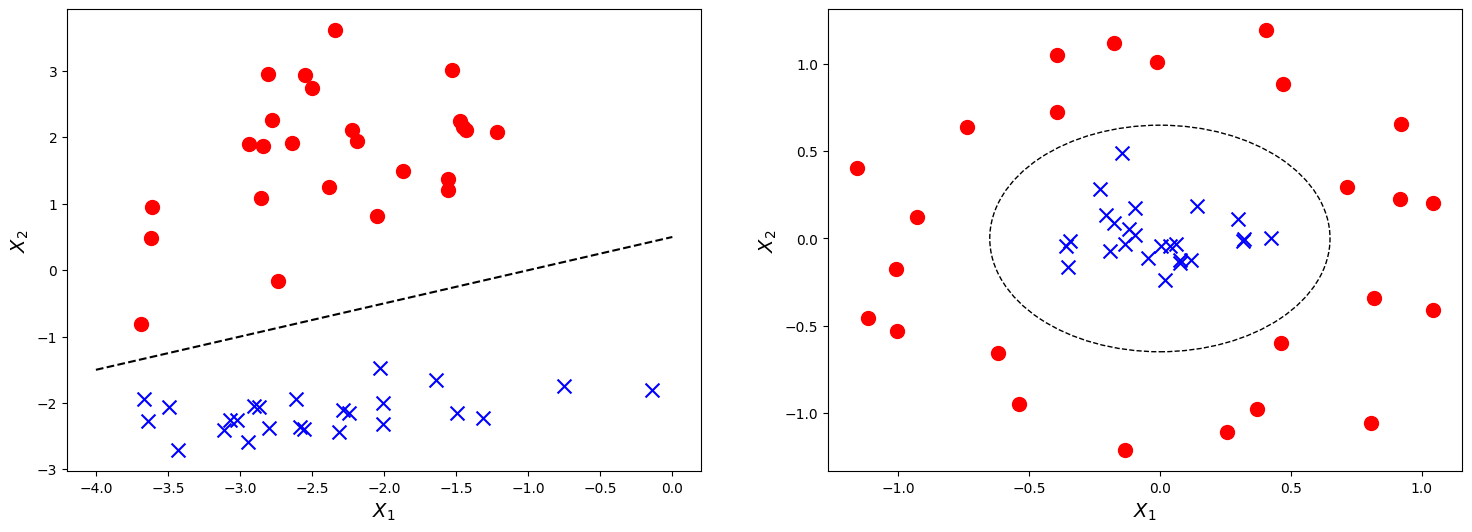
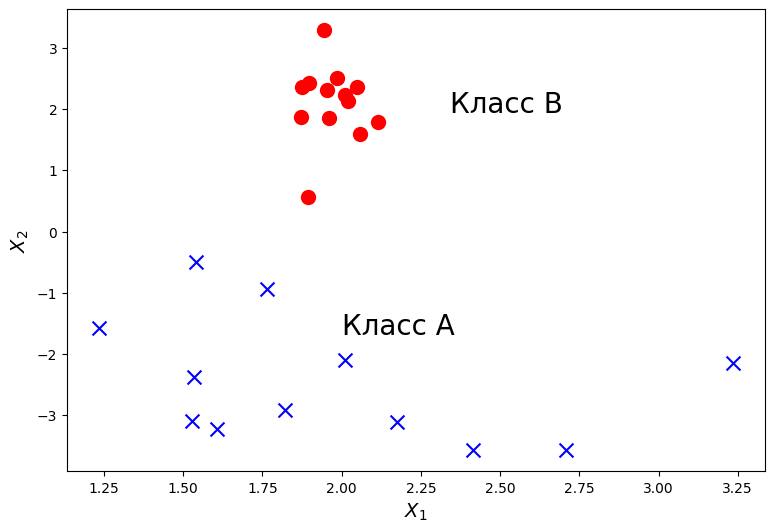
Такое свойство датасета называется линейной разделимостью. Имейте в виду, что это свойство именно данных, а не модели. На рисунке слева вы видите линейно разделимые данные, а справа - неразделимые. И логистическая регрессия хорошо работает именно на линейно разделимых данных. Поэтому важным этапом предварительного анализа данных является анализ, разделимы ли данные линейно. От этого зависит, какие модели на них будут хорошо работать.

И не забывайте, что данные у нас обычно многомерны. Это значит, что нельзя так просто нарисовать их на графике и понять визуально, разделимы они или нет. Ведь двумерный график - это лишь проекция многомерного многообразия на определенные оси. И то, что разделимо в высших размерностях может не показаться таким в проекции.

Если данные не являются линейно разделимыми, в них есть существенная нелинейная составляющая, то логистическая регрессия будет на них работать уже не так эффективно. Точно также, как линейная регрессия плохо работает, если зависимость между факторами и целевой переменной описывается нелинейной функцией. В таком случае к этим данным нужно пробовать применять другие, более сложные виды моделей. О них мы поговорим в следующих главах.

Функция ошибки и градиентный спуск для логистической регрессии

Для использования логистической регрессии как модели машинного обучения нужно определить алгоритм обучения, то есть подбор оптимальных параметров. Для этого мы будем использовать тот же алгоритм градиентного спуска, который изучали применительно к линейной регрессии. В его основе - манипулирование функцией ошибки модели, которая показывает, насколько модель соответствует данным.

Напомним, какие параметры есть у модели логистической регрессии. Сама логистическая функция параметров не имеет. Численные параметры есть только в линейной функции, которая подается на вход логистической:

Для формы логистической кривой эти параметры имеют физический смысл, также как и для линейной функции. Рассмотрим уже знакомую нам логистическую кривую (сигмоиду):

Если изменить свободный параметр, это будет иметь эффект сдвига сигмоиды в горизонтальном направлении:

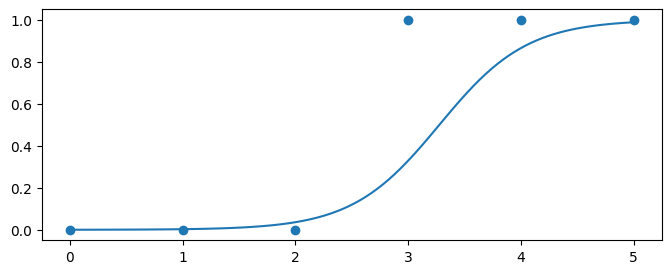
Параметр же при входной переменной ($b_1$) имеет эффект сжатия или расширения сигмоиды:

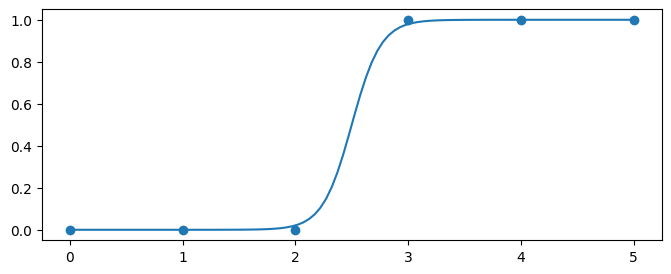
Таким образом, варьируя параметры линейной функции, мы можем изменять форму сигмоиды. Наша задача в том, чтобы найти такие значения параметров $b$, чтобы значения сигмоиды были для положительных объектов близки к 1, а для отрицательных - близки к 0. Именно такое положение сигмоиды будет соответствовать малой ошибке модели. А вот если сигмоида не “ложится в точки” - это будет означать высокую ошибку модели.

К сожалению, мы уже не можем использовать ту же самую функцию ошибки, которую мы используем для линейной регрессии, потому что логистическая функция породит немонотонную производную, имеющую множество локальных оптимумов. Другими словами, это не будет выпуклая функция.

Вместо этого функция ошибки для логистической регрессии выглядит немного сложнее. Начнем ее рассматривать с самого начала. Также, как и в прошлом случае, ошибка всей модели строится как среднее из ошибок, измеренных в каждой точке данных. Это можно записать с помощью условных обозначений так:

А вот сами индивидуальные ошибки будут строиться немного по-другому. Напомним, что сейчас мы рассматриваем индивидуальные точки данных. Для начала рассмотрим случай, когда истинное значение целевой переменной равно 1, то есть данный объект принадлежит положительному классу. Тогда мы хотим, чтобы значение логистической функции было как можно ближе к 1. Чем ближе значение сигмоиды к единице, тем меньше для нас будет ошибка. В предельном случае, когда значение будет равно единице (такое невозможно, так как сигмоида только стремится к единице, но никогда не достигает ее), ошибка должна быть нулевой. А если значение сигмоиды приближается к нулю, то это значит, что ошибка растет. Чем ближе к нулю, тем больше ошибка. Если значение логистической функции равно нулю (также в пределе), то ошибка бесконечна. для моделирования такого поведения опять-таки можно использовать разные функции, но традиционно в логистической регрессии применяются логарифмы. Если взять логарифм с противоположным знаком, то мы добьемся как раз нужного эффекта. Так что если $y=1$, то ошибка в конкретной точке будет записываться так:

Для противоположного случая, когда $y=0$, то есть объект принадлежит отрицательному классу, ситуация прямо противоположная. Нужно считать, что ошибка нулевая, если значение сигмоиды равно нулю, а если оно равно единице - то ошибка бесконечна. Для этого можно просто взять логарифм от $1 - g(z)$. Обратите внимание, что это имеет смысл, так как мы точно знаем, что значение сигмоиды всегда лежит от 0 до 1 (не включая концы). Поэтому нам неважно, как ведет себя функция ошибки, если ее аргумент будет какой-то другой, вне этого диапазона. Итак, для второго случая индивидуальная ошибка будет вычисляться так:

Чем больше конкретная функция гипотезы отклоняется от реального значения $y$, тем больше получающая функция ошибки. Если гипотеза равна истинным значениям $y$, то ошибка равна 0. Это поведение функции ошибки в индивидуальной точке можно понять, посмотрев на два графика, которые иллюстрируют поведение функции ошибки в зависимости от аргумента сигмоиды, то есть линейной комбинации:

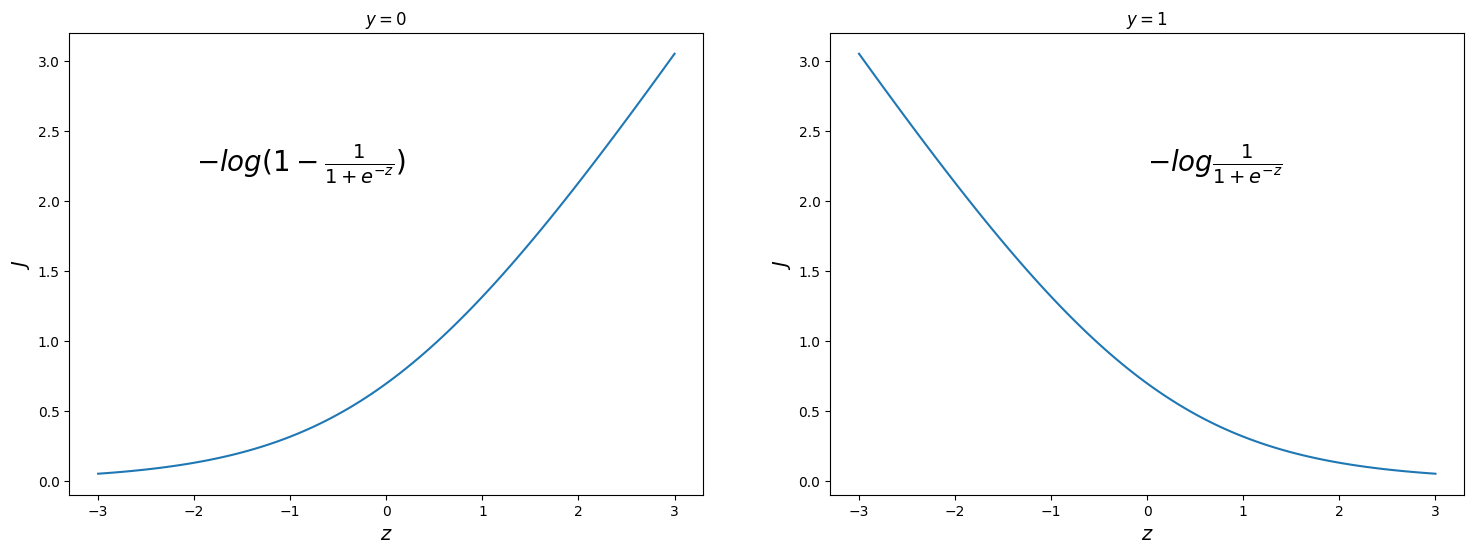
Мы можем представить два рассмотренных условных случая функции ошибки в одно выражение, используя тот факт, что истинные значения $y$ могут принимать только значения 0 или 1:

Обратите внимание, что когда $y$ равно 1, то второе слагаемое будет равен нулю и не повлияет на результат. Если $y$ равно 0, то, наоборот, первое слагаемое будет равен нулю и не повлияет на результат. Это математическию трюк позволяет выразить функцию в виде единой формулы, а не набора условных выражений, как в кусочных функциях. Это очень полезно и удобно для последующих манипуляций с этой функцией.

Заметим, что при такой функции ошибки она в каждой точке будет ненулевая. Идеальный случай, когда ошибка равна нулю недостижим на практике, так как значение сигмоиды только бесконечно приближается к границам (значениям 0 и 1), но никогда не может достичь их. Именно такая функция ошибки имеет несколько критичных преимуществ перед какими-нибудь другими, которые мы могли бы изобрести. Во-первых, она будет выпукла, то есть иметь один глобальный оптимум, как в случае с линейной регрессией. Во-вторых, она везде дифференцируема, так как использует только гладкие функции, мы смогли даже избавиться от кусочности, представив ее в виде одного выражения. И в-третьих, при ее дифференцировании функции логарифма и экспоненты в какой-то момент прекрасно сократятся, что значительно упростит выражение для градиента.

Мы можем полностью сформулировать общую функцию ошибки следующим образом:

Для дифференцирования этой функции выразим ее в явном виде:

Теперь для полноценного определения алгоритма градиентного спуска нужно взять частные производные этой функции по всем параметрам. Продифференцировав ее найдем частную производную функции ошибки:

Теперь заметим, что данное выражение содержит в себе формулу функции модели. Запишем ее через функцию гипотезы:

Обратите внимание, что мы получили точно такое же выражение, что и в случае с линейной регрессией. Также, как и в том случае, формула для частной производной выражена через функцию гипотезы. И опять же это не случайно. Так мы получаем, что алгоритм градиентного спуска полностью аналогичен для логистической и для линейной регрессии.

Напомним, что общая форма градиентного спуска:

Подставляя выражение для частной производной получаем следующее выражение:

Обратите внимание, что этот алгоритм полностью идентичен тому, который мы использовали в линейной регрессии. Именно поэтому мы выразили эту формулу в терминах функции гипотезы, не раскрывая дальше $h_b(x)$. Также, как и раньше метод градиентного спуска подразумевает, что нужно обновлять все значения $b$ одновременно.

Многоклассовая классификация: один против всех

До сих пор мы рассматривали алгоритм логистической регрессии, который может решать только проблему бинарной классификации. Более того, некоторые математические выкладки активно используют тот факт, что целевая переменная может принимать только значения 0 или 1. Как же его безболезненно обобщить на случай, когда классов больше? Теперь мы рассмотрим классификацию данных более чем в двух категориях. Вместо $y = \lbrace 0, 1 \rbrace$ мы расширим наше определение так, чтобы

Пример набора данных для задачи множественной классификации, содержащих два признака и три класса можно увидеть на рисунке:

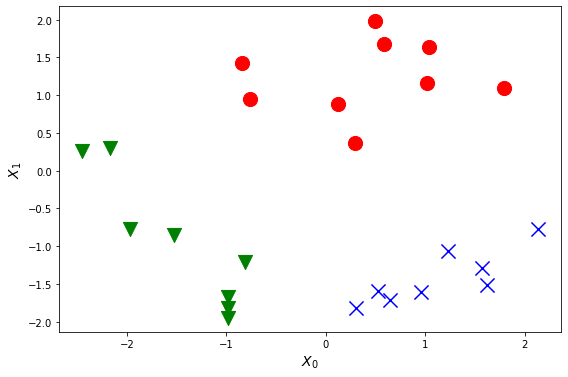
Алгоритм классификации в данном случае очень прост. Мы берем последовательно каждый имеющийся класс в данных, делаем его “положительным”, а все остальные - “отрицательными”, и обучаем модель, которая стремится отделить данный класс от остальных. Схематично алгоритм классификации “один против всех” можно увидеть на рисунке:

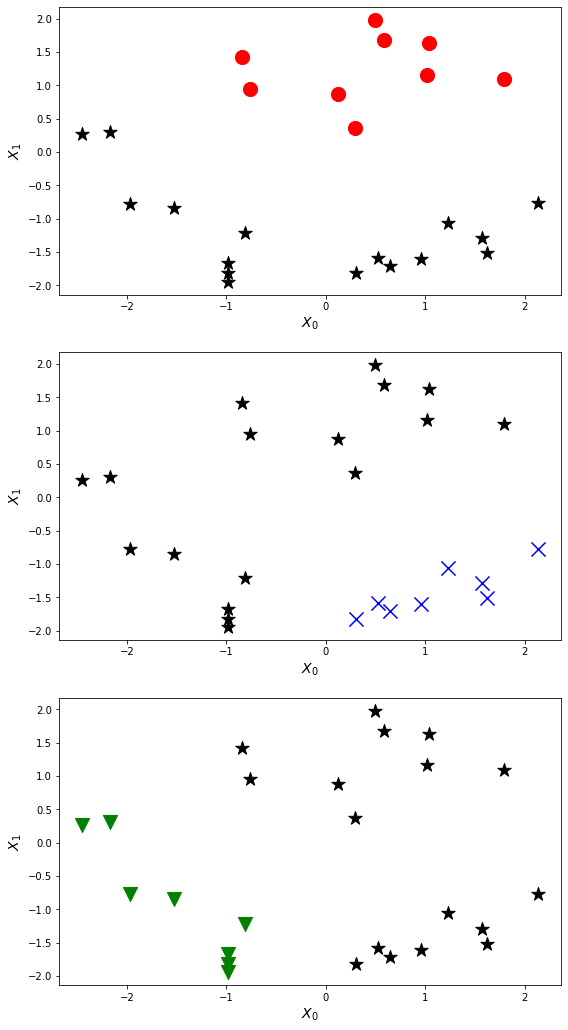
В этом случае мы делим нашу задачу на $ n + 1 $ (потому что индекс начинается с 0) бинарных задач классификации. В каждом из них мы прогнозируем вероятность того, что $y$ является членом одного из наших классов. То есть мы обучаем сразу множество моделей, столько, сколько у нас есть классов. Так что на каждый класс в задаче будет своя собственная модель, которая для определенного объекта выдает вероятность принадлежности этого объекта к соответствующему классу. Для каждого конкретного объекта все модели выдают такой вектор вероятностей:

Другими словами, построив несколько моделей бинарной классификации мы можем использовать их, чтобы получить оценки вероятности принадлежности любого объекта ко всем имеющимся классам. После этого для окончательной классификации выбирается тот класс, чья модель дала наивысший результат. Другими словами, мы с помощью нескольких моделей оцениваем, к какому классу вероятнее всего принадлежит данный объект и выбираем для окончательной классификации тот класс, чья вероятность выше остальных.

Данный метод называется “один против всех” (one vs all или one vs rest). Это название подчеркивает тот факт, что для каждого класса оценивается вероятность принадлежности объекта к нему, в сравнении с вероятностью принадлежности к любому из всех остальных классов. Надо отметить, что во всех современных программных инструментах для машинного обучения, он уже реализован и встроен в существующие методы классификации, так что разработчику не придется программировать его специально.

Кроме того, чуть позже мы познакомимся с моделями, которые сами по себе способны решать задачи множественной классификации, а значит, не требуют реализации схемы “один против всех”. Она нужна только для моделей, которые способны решать только бинарную классификацию, чтобы “приспособить” их для задач, где классов больше двух.

Обратите внимание, что формулировка данного алгоритма не предполагает использование порогового значения. Вероятности принадлежности объекта к классам могут быть любые. Нам важно выбрать среди них максимум. Даже есть все эти вероятности меньше 50%, все равно мы выберем тот класс, к которому данный объект больше всего подходит. Более того, в среднем, эти вероятности обратно пропорциональны количеству классов в задаче. То есть если в конкретной проблеме, например, 50 000 классов, то не стоит ожидать, что объект будет принадлежать одному из них с вероятностью 90%. Здесь скорее речь пойдет о выборе между 0,028% и 0,025%.

У этого алгоритма есть еще одна характерная черта. С его помощью можно решать задачи мультиклассификации. Напомним, это такие, в которых один конкретный объект может принадлежать нескольким классам одновременно. Такие задачи часто формулируются как придание объекту набора меток. Например, добавление релевантных тегов к посту в социальных сетях. Естественно, что у отдельно взятому посту можно придать достаточно много тегов. В данном случае теги служат классами, но задача мультиклассовая. Другой пример - распознавание объектов на изображении. На конкретной картинке может же быть не один объект, а несколько, произвольное количество. Так вот, при использовании алгоритма “один против всех” можно брать как итоговый не один класс с максимальной вероятностью, а сразу несколько. Стратегии отбора классов бывают разные: в одной задаче можно брать фиксированное количество лучше подходящих классов, в других - брать любое количество классов, вероятности которых больше определенного порога.

Конечно, есть у данного алгоритма и оборотная сторона. Его применение не очень целесообразно, если в задачу уж очень большое количество классов. Ведь тогда придется обучить и использовать точно такое же количество моделей. А это может быть как затратно по процессорному времени, то есть обучение будет проходить слишком медленно, так и затратно по памяти, ведь все эти модели, их параметры надо хранить для осуществления предсказания. Может, стоит рассмотреть другие виды моделей классификации, которые решают множественные задачи сами по себе.

Практическое построение классификации

Как подготовить данные для классификации?

Для решения задач классификации в языке программирования Python с использованием sklearn остается справедливым все то, о чем мы говорили в конце предыдущей части о подготовке данных для регрессионных задач. Так же нам нужно сформировать два массива данных - двумерный массив признаков X и одномерный массив значений целевой переменной y.

Раньше, в векторе значений целевой переменной находились сами численные значения. В данных для классификации метки классов могут обозначаться разными способами - числом, названием, аббревиатурой. Дальше мы будем подразумевать, что значения в массиве y заданы просто числами - [0, 1], если классов два (бинарная классификация), [0, 1, 2] - если классов три и так далее. Если в вашем датасете это не так и классы обозначаются как-то по другому, то обратитесь к одной из следующих частей, где мы обсуждаем преобразование и подготовку данных.

Здесь хотелось бы упомянуть еще об одной полезной функции библиотеки sklearn - процедурной генерации датасетов. Данная библиотека включает в себя несколько функций, которые используются для создания случайных наборов данных для тестирования моделей машинного обучения. В частности, существует функция make_classification, которая позволяет быстро создать случайный набор данных для классификации, обладающий определенными свойствами. Вы можете настроить количество точек, количество классов и признаков, насколько они будут линейно разделимы. Более полно информацию об этой и других функциях смотрите в официальной документации sklearn, в разделе, посвященном пакету datasets. Приведем пример использования этой функции:

1
2
3
from sklearn.datasets import make_classification

X, Y = make_classification( n_features=2)

В результате мы получаем и массив признаков и вектор значений целевой переменной. Они уже готовы для использования в моделях классификации.

Если возможно, всегда нужно стремится визуализировать данные, которые вы собираетесь анализировать. В случае с данными для классификации это немного сложнее, чем для парной регрессии, ведь нам нужно на графике как-то выделить классы. Можно воспользоваться встроенной возможностью задания цвета точек через массив вот так:

1
2
plt.scatter(X[:, 0], X[:, 1], marker="o", c=Y, s=25, edgecolor="k")
plt.show()

Обратите внимание, что в данном случае мы явно указываем, какие признаки будут расположены по осям. В данном примере мы откладываем первый столбец (с индексом 0) по горизонтальной оси, а второй (с индексом 1) - по вертикальной. Вот так это выглядит на графике:

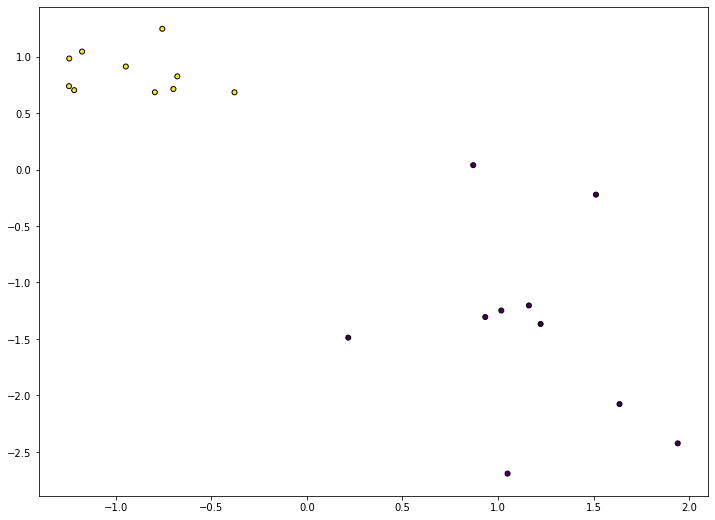
Есть другой способ - визуализировать каждый класс отдельно. В таком случае мы можем более гибко управлять отображением разных классов - задавать явно произвольные цвета, размеры, форму маркеров точек. Обратите внимание, как в данном примере используется условная индексация одного массива (признаков) другим массивом (целевой переменной):

1
2
3
plt.scatter(X[:, 0][Y==0], X[:, 1][Y==0], marker="o", c='r', s=100)
plt.scatter(X[:, 0][Y==1], X[:, 1][Y==1], marker="x", c='b', s=100)
plt.show()

Вот так это выглядит на графике:

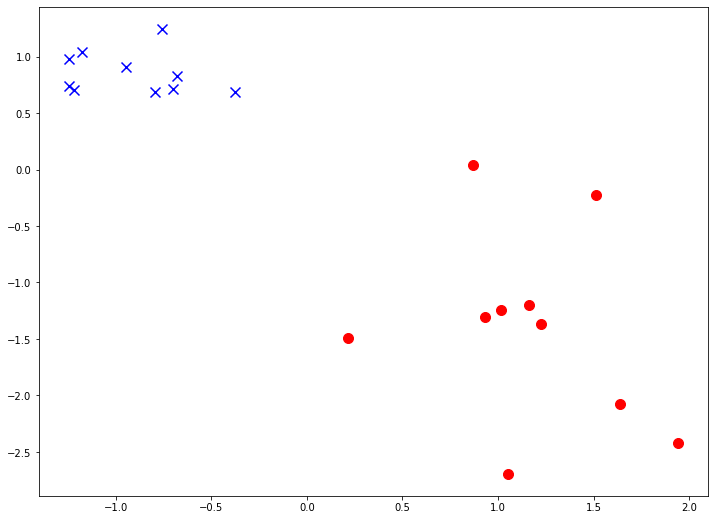
Помимо визуализации с данными такой структуры можно работать абсолютно так же, как и с данными для регрессии.

Как реализовать логистическую регрессию?

Рассмотрим простейшую модель логистической регрессии. Как мы увидели в этой главе, она мало чем отличается от модели линейной регрессии, поэтому возьмем за основу класс, который реализовали в предыдущей части, посвященной задаче регрессии.

Мы будем рассматривать двумерную задачу классификации. То есть у нас будет два непрерывных признака - $x_1$ и $x_2$. Поэтому в модели будет 3 параметра - $b_0, b_1, b_2$. Еще мы предполагаем решение бинарной задачи, так как множественная классификация решается отдельным алгоритмом “один-против-всех”

Ключевым отличием метода predict будет то, что мы считаем линейную комбинацию, а затем считаем логистическую функцию от нее:

1
2
3
def predict(self, x):
    x1, x2 = x
    z = self.b0 + self.b1 * x1 + self.b2 * x2

Модифицируем функцию ошибки так, чтобы она соответствовала формуле логарифмической ошибки для логистической регрессии:

1
2
def error(self, X, Y):
    return -sum(Y * np.log2(self.predict(X)) + (1 - Y) *(1 - np.log2(self.predict(X)))) / len(X[0])

Теперь перейдем к методу градиентного спуска. И вот здесь все останется поразительно похожим на линейную регрессию, за исключением большего количества параметров:

1
2
3
4
5
6
7
8
9
def BGD(self, X, Y):  
    alpha = 0.5
    for _ in range(1000):
      dJ0 = sum(self.predict(X) - Y) /len(X)
      dJ1 = sum((self.predict(X) - Y) * X[0]) /len(X[0])
      dJ2 = sum((self.predict(X) - Y) * X[1]) /len(X[0])
      self.b0 -= alpha * dJ0
      self.b1 -= alpha * dJ1
      self.b2 -= alpha * dJ2

Полностью код, реализующий метод логистической регрессии, выглядит так:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class hypothesis(object):
    """Модель логистической регрессии"""
    def __init__(self):
        self.b0 = 0
        self.b1 = 0
        self.b2 = 1
    def predict(self, x):
        x1, x2 = x
        z = self.b0 + self.b1 * x1 + self.b2 * x2
        return 1 / (1 + np.exp(-z))
    def error(self, X, Y):
        return -sum(Y * np.log2(self.predict(X)) + (1 - Y) *(1 - np.log2(self.predict(X)))) / len(X[0])
    def BGD(self, X, Y):  
        alpha = 0.5
        for _ in range(1000):
          dJ0 = sum(self.predict(X) - Y) /len(X)
          dJ1 = sum((self.predict(X) - Y) * X[0]) /len(X[0])
          dJ2 = sum((self.predict(X) - Y) * X[1]) /len(X[0])
          self.b0 -= alpha * dJ0
          self.b1 -= alpha * dJ1
          self.b2 -= alpha * dJ2

Обратите внимание на задание начальных значений параметров. В данном примере мы создаем регрессию со следующими значениями параметров по умолчанию: $b_0 = 0; b_1 = 0; b_2 = 1$. Задание одного из параметров в 1 нужно будет потом, чтобы получился более понятный график модели без обучения. На практике можно задавать начальные значения всеми нулями.

Как оценить качество классификационной модели?

После создания модели логистической регрессии логичным шагом будет вывести ее на график вместе с точками данных. Проблема в том, что это не так просто, как в случае с линейной регрессией, так как мы имеем два измерения признаков плюс еще значение самой функции модели. Для того, чтобы наглядно увидеть, как сочетается значение модели с точками воспользуемся построением контурного графика.

Для начала создадим экземпляр модели с параметрами по умолчанию:

1
2
3
4
hyp = hypothesis()
print(hyp.predict((0, 0)))
J = hyp.error(X, Y)
print("initial error:", J)

Теперь надо подготовить равномерные данные для рисования функции гипотезы. Нам понадобится создать двумерную сетку. К счастью, в numpy есть необходимые элементы. Подробный разбор кода выходит за рамки данного пособия, так как использует продвинутые возможности библиотеки numpy. Если вам интересно, как работает этот код, обратитесь к документации к используемым методам:

1
2
3
4
xx, yy = np.meshgrid(
    np.arange(X.min(axis=0)[0]-1, X.max(axis=0)[0]+1, 0.01), 
    np.arange(X.min(axis=0)[1]-1, X.max(axis=0)[1]+1, 0.01))
XX = np.array(list(zip(xx.ravel(), yy.ravel()))).reshape((-1, 2))

В данном коде мы создаем двумерную матрицу, содержащую все комбинации значений признаков в заданном диапазоне. Другими словами, мы создаем равномерную сетку в прямоугольнике от минимального до максимального значения каждого признака (отступая для красоты 1 в обоих направлениях). Попробуйте вывести получившиеся переменные, чтобы понять принцип построения данной сетки. А после мы используем матрицу XX как исходные данные для модели:

1
2
Z = hyp.predict(XX)
Z = Z.reshape(xx.shape)

Данный код выполнит предсказание модели в каждой точке нашей сетки. Эти данные мы сможем использовать для того, чтобы построить контурный график вот так:

1
2
3
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0][Y==0], X[:, 1][Y==0], marker="o", c='r', s=100)
plt.scatter(X[:, 0][Y==1], X[:, 1][Y==1], marker="x", c='b', s=100)

В итоге мы должны получить график, похожий на следующий рисунок:

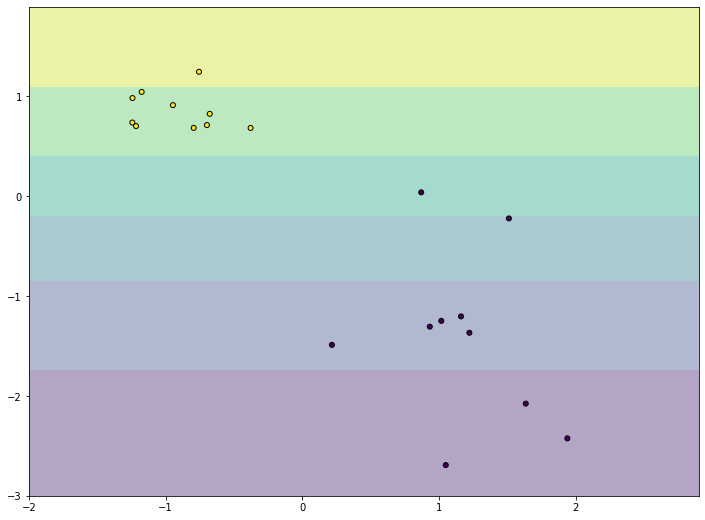
На графике мы видим наши точки данных, они выглядят так же, как и в предыдущих частях. Кроме него график заполняет заливка цветом. Цвет показывает значение функции гипотезы в данной точке. Так как мы задавали начальные значения параметров модели специально, параметр $b_2 = 1$ дает нам такой ровный градиент, который увеличивается равномерно с ростом значения признака $x_1$. Конечно, такой градиент никак не учитывает положение точек. Это и логично, ведь наша модель еще не обучена. Давайте запустим градиентный спуск и увидим модель после обучения:

1
2
3
4
5
6
7
8
hyp.BGD(X, Y)

Z = hyp.predict((xx, yy))
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X.T[:, 0], X.T[:, 1], marker="o", c=Y, s=25, edgecolor="k")
plt.show()

Обратите внимание, что мы переиспользуем сетку, которую создавали на предыдущем шаге. Ведь сами значения не меняются, меняется только набор значений модели. После обучения вы должны увидеть примерно такой график:

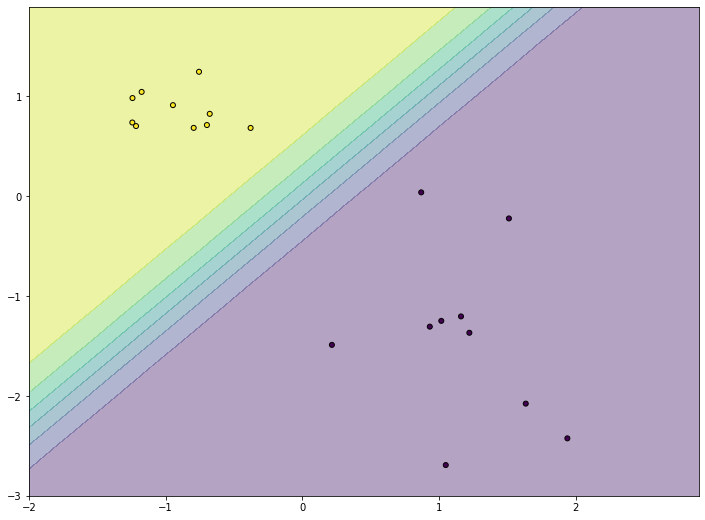
На нем мы видим, что функция гипотезы подстроилась к точкам таким образом, чтобы для точек положительного класса (желтых) выдавать значения, близкие к единице (желтая область), а для точек отрицательного класса (черных) - значения, близкие к нулю (фиолетовая область). То есть модель стала гораздо лучше соответствовать данным. Посередине между двумя областями мы видим более узкую полоску градиента. Это область, для точек которой модель не уверена в своих предсказаниях и выдает значения, ближе к 0,5. Именно в этой полосе располагается граница принятия решения нашей модели.

Как построить простую классификацию в scikit-learn?

Так же, как и в случае с линейной регрессией, самостоятельная реализация данного метода нужна только для того, чтобы на практике прочувствовать алгоритм его работы. В реальной жизни лучше всего пользоваться существующими профессиональными реализациями. Именно поэтому мы используем sklearn. Работа с моделью классификации в этой библиотеке практически не отличается от работы с линейной регрессией. Для начала нужно импортировать нужный класс, создать его экземпляр и обучить его на имеющихся данных:

1
2
3
4
5
6
7
from sklearn import linear_model

X = X.T

reg = linear_model.LogisticRegression()
reg.fit(X, Y)
print(reg.score(X, Y))

Обратите внимание, на то, что названия методов полностью совпадают у всех моделей машинного обучения в этой библиотеке. За счет этого ей очень приятно и просто пользоваться - у всех моделей единый интерфейс.

Точно так же, как и в самостоятельной реализации мы можем использовать модель для построения предсказания по сетке и для построения контурного графика. Давайте сравним самостоятельную реализацию логистической регрессии с библиотечной:

1
2
3
4
5
6
7
Z = reg.predict(XX)
Z = Z.reshape(xx.shape)

plt.figure(figsize=(12, 9))
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0][Y==0], X[:, 1][Y==0], marker="o", c='r', s=100)
plt.scatter(X[:, 0][Y==1], X[:, 1][Y==1], marker="x", c='b', s=100)

В результате выполнения данного кода вы должны увидеть график наподобие следующего:

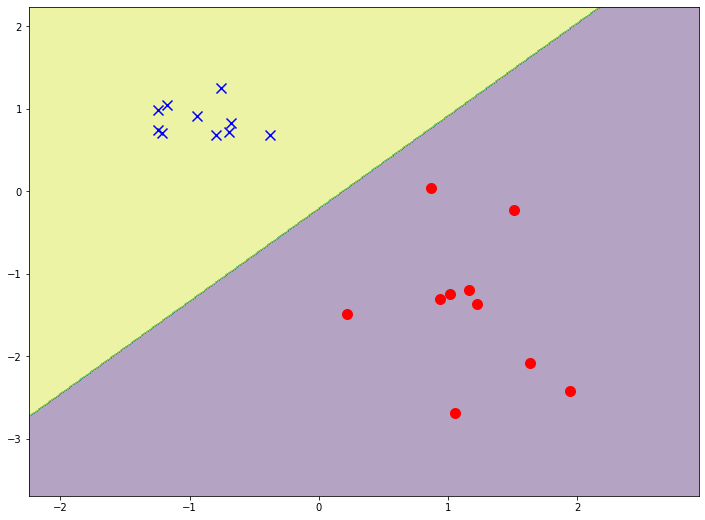
Обратите внимание, что граница принятия решения расположена примерно в том же месте, что и у нашей реализации. Однако полоса “неопределенности”, область, где проявляется цветовой градиент, значительно уже. На библиотечной модели ее вообще почти невозможно разглядеть. Это не значит, что наша модель обучилась хуже. Ведь наша модель все еще способна точно отделить точки обучающей выборки разных классов. Но библиотечная модель обучилась “сильнее” - она более уверенно классифицирует точки, которые ближе к границе принятия решения.