Линейные модели
В предыдущих главах мы изучили применение метода линейной регрессии для предсказания непрерывной целевой переменной и логистической регрессии для решения задач классификации. Можно заметить, что по сути это одна и та же модель, но немного по-другому использующаяся при решении разных задач. В основе обеих этих моделей лежит использование линейной функции. Мы подбираем параметры этой линейной функции таким образом, чтобы она удовлетворяла определенным оптимизационным критериям. И вот сами эти критерии различаются для задач регрессии и классификации.
И в той и в другой задаче мы имеем обучающую выборку, которую можно представить как некоторое множество точек в многомерном пространстве. Причем, в задачах регрессии мы обычно воспринимаем целевую переменную как еще одно измерение. Поэтому на двумерных графиках мы часто изображаем регрессию от одной переменной (то есть с одним атрибутом x, одной колонкой в наборе данных) - вместе с целевой переменной получится как раз два измерения. А вот в задачах классификации значения целевой переменной, то есть класс объекта, обычно не воспринимается как отдельное измерение, а как некоторая встроенная характеристика точки. Поэтому мы можем легко изобразить на двумерном графике задачу классификации на двух признаках ($x_1$ и $x_2$) - ведь метку класса мы изображаем как цвет или форму точки.
Но помните, как в начале прошлой части учебника мы пытались изобразить классификацию также как регрессию - откладывая целевую переменную по одной из осей? На самом деле размерность задачи определяется только количеством признаков, независимо от того, какую задачу мы решаем. Если у нас один признак - то мы имеем распределение точек на плоскости. Если два - в пространстве, а если больше - в гиперпространстве. Представить это становится все труднее, поэтому мы учимся на примерах маленькой размерности. Важно понять, как устроены модели и методы, а математический аппарат способен обобщить наши подходы на произвольное количество измерений.
А линейные модели устроены таким образом, что они описывают некоторое линейное подпространство с размерностью, на единицу меньшей, чем размерность всей задачи в целом. Если в модели один признак - то линейная функция будет представлять собой прямую в той плоскости, в которой лежат точки такой двумерной задачи. Если два признака - то плоскость и пространстве трехмерной задачи (как на рисунке ниже). А если признаков больше - то гиперплоскость, вложенную в гиперпространство.

В любом случае мы находим линейную комбинацию координат этих точек с вектором весов, то есть по сути, некоторую гиперплоскость в этом многомерном пространстве. Однако то, какая именно линейная комбинация, будет для нас оптимальной, то есть какие коэффициенты в линейной функции мы хотим получить, зависит от задачи. Если мы решаем задачу регрессии, то мы строим линию таким образом, чтобы она лучше всего легла в точки. Причем здесь имеется в виду распределение точек вместе с целевой переменной. Как мы уже изучали, для этого нам нужна функция ошибки. То есть мы сравниваем значение функции гипотезы (модели) с истинными значениями целевой переменной и подбираем параметры модели таким образом, чтобы эти отклонения были как можно меньше.
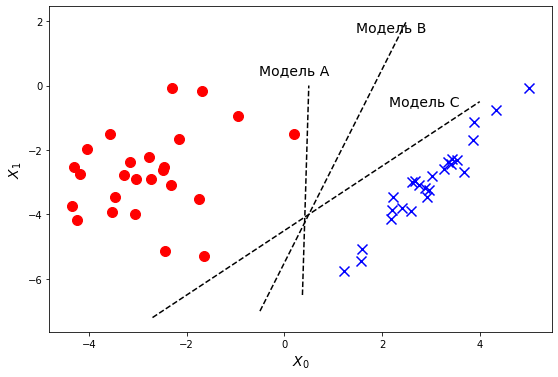
Немного другая ситуация с классификацией. Линейная модель также формирует гиперплоскость, но на этот раз мы не рассматриваем целевую переменную как еще одно измерение. То есть граница принятия решения должна быть на одно измерение меньше, чем размерность самой задачи. И мы как раз это и видим - для классификации нам не очень важно само значение функции гипотезы, нам важна область точек, в которых она равна 0. Эта область как раз и формирует границу принятия решения.
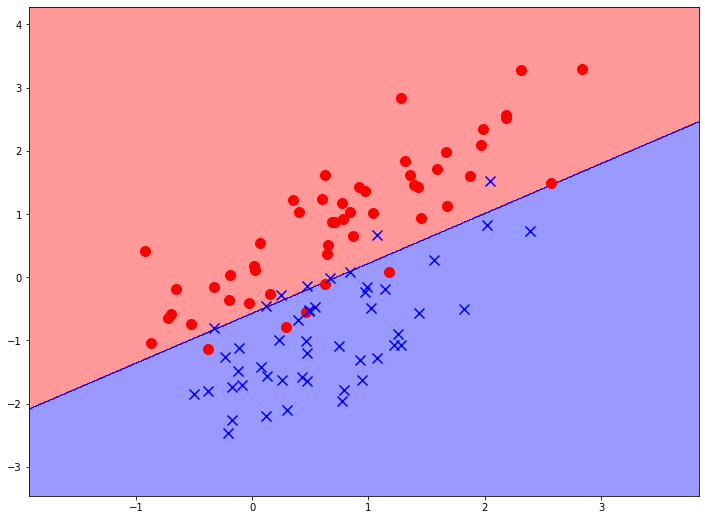
Логистическая функция здесь нужна только для того, чтобы более надежно реализовать оптимизацию параметров методом градиентного спуска. Для точек, которые лежат по одну сторону границы мы хотим, чтобы линейная функция принимала положительные значения, а, соответственно, логистическая модель - значения, близкие к единице. И мы хотим, чтобы граница принятия решения располагалась таким образом, чтобы по эту сторону от нее располагались те точки, которые в обучающей выборке отнесены к положительному классу.
Другими словами, линейная и логистическая регрессии - суть одна и та же модель, использующаяся в разных условиях и с разными задачами. Поэтому, кстати, логистическая регрессия является линейной моделью. Вообще, стоит говорить об одном классе моделей - линейных моделей - которые применяются как к задачам регрессии, так и к задачам классификации.
Это справедливо и по отношению к другим классам моделей, которые мы будем рассматривать в данной главе. Очень редкие модели можно применять только к задачам классификации или к задачам регрессии. Мы вообще изучим только один такой пример - наивный байесовский классификатор, который по своей сути нельзя применить к регрессионным задачам. А в большинстве совем одни и те же модели могут использоваться для решения как задач предсказания дискретного, так и непрерывного значения.
Поэтому мы не говорим отдельно об алгоритмах классификации или моделях регрессии. Есть модели обучения с учителем. Именно поэтому, кстати, в документации к библиотеке sklearn вы не найдете отдельных частей, посвященных регрессии и классификации. Есть глава, посвященная линейным моделям, методу опорных векторов и так далее. И мы дальше будем изучать модели исходя именно из этой логики.
Так как мы теперь говорим об общем классе линейных моделей, выделим главные их черты, которые отличают в практическом применении их от других видов моделей и алгоритмов машинного обучения. В первую очередь надо сказать, что линейные модели - это самый простой класс моделей. Это свидетельствует не только о примитивности (низкой вариативности) самого класса линейных функций. Главное - что линейные модели достаточно быстро обучаются. Существуют алгоритмы. которые требуют гораздо больших вычислительных мощностей для своей работы. Это несомненное преимущество линейных моделей.
Но из их простоты следует и главный недостаток. Линейные модели могут описать только линейные зависимости в данных. Для задач регрессии это означает, что линейные модели хорошо описывают данные, в которых присутствует линейная корреляция между признаками и целевой переменной. Если же в данных нет корреляции, либо зависимость имеет нелинейный характер, то линейные модели в принципе не способны хорошо (то есть с низкой ошибкой) описать это набор данных. Для задач классификации аналогичное свойство - линейная разделимость. Если граница между разными классами носит явно нелинейный характер, то логистическая регрессия просто не справится с разделением данных по классам.
Надо помнить, что линейные зависимости в данных не означает, что данные точно описываются линейной функцией. Бывают ситуации, когда данные может быть формально и не являются линейно неразделимыми (в случае с классификацией) или не лежат на одной прямой (для регрессии), но явно демонстрируют линейную зависимость. Ведь мы строим модель, чтобы она научилась выявлять общие зависимости в данных, но в них часто есть и случайные колебания, которые не должны влиять на результат моделирования.
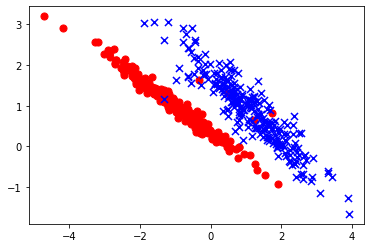
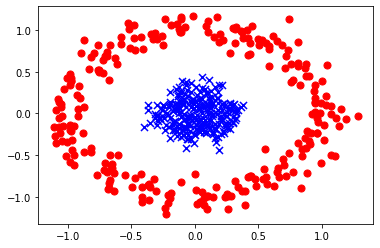
Сравните, например, такую картинку со следующей. На обоих изображены линейно неразделимые наборы данных. Но мы совершенно правильно интуитивно понимаем, что на верхнем графике изображены данные, которые очень хорошо будут описаны линейной моделью. И неважно, что несколько точек мы классифицируем неправильно. Даже наоборот, было бы хуже пытаться построить модель, которая бы учитывала эти аномальные точки и строила бы очень сложную границу принятия решений.
Еще одно достоинство, общее для линейных моделей - их интерпретируемость. Параметрами линейных моделей являются коэффициенты при признаках (плюс еще свободный коэффициент). И в любой реальной задаче признаки имеют какую-то интерпретацию, физический смысл. Поэтому их коэффициенты тоже можно объяснить в терминах предметной области. Коэффициент каждого признака показывает, на сколько изменится значение целевой переменной при изменении данного признака на единицу. То есть коэффициент косвенно показывает силу связи признака и целевой переменной. Если признак не влияет на нее, то его коэффициент будет стремиться к нулю. А свободный параметр показывает уровень целевой переменной при нулевых значениях признака.
Интерпретируемость модели машинного обучения - это очень важная характеристика, особенно в некоторых серах применения, например, в медицинской диагностике, государственном управлении, социальной сфере. В таких предметных областях нужно не просто строить качественные модели, но и уметь объяснять их предсказания, понимать, почему и за счет чего было принято такое решение. Поэтому при прочих равных более интерпретируемая модель всегда будет предпочтительнее.
Выводы:
- Линейные модели могут служить как моделями классификации, так и моделями регрессии.
- По сути, это одна модель, которую приспосабливают для решения разных задач.
- Линейная модель - это результат вычисления линейной комбинации признаков и параметров: $ h_b (x) = X \cdot \vec{b} $
- Для задач регрессии мы сравниваем результат $ X \cdot \vec{b} $ с $ y $.
- Для задач классификации мы строим разделяющее множество $ X \cdot \vec{b} = 0 $.
- Эффективность линейных моделей зависит от структуры данных (для регрессии это должна быть линейная корреляция, для классификации - линейная разделимость).
- Линейные модели достаточно просты в обработке, но склонны к недообучению из-за своей простоты.
- Линейные модели интерпретируемы - их коэффициентам можно придать физический смысл.
Полиномиальные модели
Линейные модели обладают неоспоримыми достоинствами, когда мы имеем дело с датасетом определенной структуры. Например, на графике выше представлен очевидно линейно разделимый датасет. И при его анализе более сложные модели даже и не нужны, со всем справится простая логистическая регрессия.
Полиномиальная регрессия
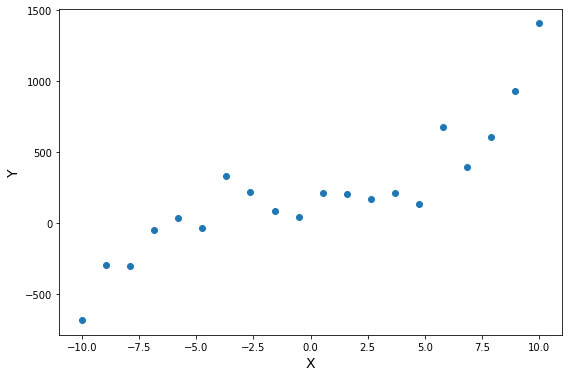
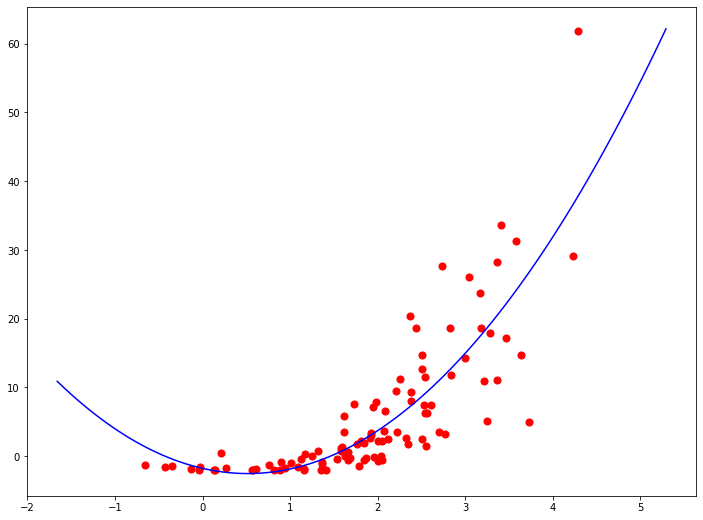
Функция гипотезы не обязательно должна быть линейной, если это не соответствует данным. На практике вы не всегда будете иметь данные, которые можно хорошо аппроксимировать линейной функцией. Наглядный пример вы видите на иллюстрации. Вполне очевидно, что в среднем увеличение целевой переменной замедляется с ростом входной переменной. Это значит, что данные демонстрируют нелинейную динамику. И это так же значит, что мы никак не сможем их хорошо приблизить линейной моделью.
Надо подчеркнуть, что это не свидетельствует о несовершенстве наших методов оптимизации. Мы действительно можем найти самую лучшую линейную функцию для данных точек, но проблема в том, что мы всегда выбираем лучшую функцию из некоторого класса функций, в данном случае - линейных. То есть проблема не в алгоритмах оптимизации, а в ограничении самого вида модели.
вполне логично предположить, что для описания таких нелинейных наборов данных следует использовать нелинейные же функции моделей. Но очень бы не хотелось, для каждого нового класса функций изобретать собственный метод оптимизации, поэтому мы постараемся максимально “переиспользовать” те подходы, которые описали выше. И механизм множественной регрессии в этом сильно поможет.
Мы можем изменить поведение или кривую нашей функции гипотезы, сделав ее квадратичной, кубической или любой другой формой.
Например, если наша функция гипотезы $ \hat{y} = h_b (x) = b_0 + b_1 x $, то мы можем добавить еще один признак, основанный на $ x_1 $, получив квадратичную функцию
или кубическую функцию
В кубической функции мы по сути ввели два новых признака: $ x_2 = x^2, x_3 = x^3 $. Точно таким же образом, мы можем создать, например, такую функцию:
В любом случае, мы из парной линейной функции сделали какую-то другую функцию. И к этой нелинейной функции можно относиться по разному. С одной стороны, это другой класс функций, который обладает нелинейным поведением, а следовательно, может описывать более сложные зависимости в данных. С другой стороны, это линейна функция от нескольких переменных. Только сами эти переменные оказываются в функциональной зависимости друг от друга. Но никто не говорил, что признаки должны быть независимы.
И вот такое представление нелинейной функции как множественной линейной позволяет нам без изменений воспользоваться алгоритмом градиентного спуска для множественной линейной регрессии. Только вместо $ x_2, x_3, … , x_n $ нам нужно будет подставить соответствующие функции от $ x_1 $.
Очевидно, что нелинейных функций можно придумать бесконечное количество. Поэтому встает вопрос, как выбрать нужный класс функций для решения конкретной задачи. В случае парной регрессии мы можем взглянув на график точек обучающей выборки сделать предположение о том, какой вид нелинейной зависимости связывает входную и целевую переменные. Но если у нас множество признаков, просто так проанализировать график нам не удастся. Поэтому по умолчанию используют полиномиальную регрессию, когда в модель добавляют входные переменные второго, третьего, четвертого и так далее порядков.
Порядок полиномиальной регрессии подбирается в качестве компромисса между качеством получаемой регрессии, и вычислительной сложностью. Ведь чем выше порядок полинома, тем более сложные зависимости он может аппроксимировать. И вообще, чем выше степень полинома, тем меньше будет ошибка при прочих равных. Если степень полинома на единицу меньше количества точек - ошибка будет нулевая. Но одновременно с этим, чем выше степень полинома, тем больше в модели параметров, тем она сложнее и занимает больше времени на обучение. Есть еще вопросы переобучения, но про это мы поговорим позднее.
А что делать, если изначально в модели было несколько признаков? Тогда обычно для определенной степени полинома берутся все возможные комбинации признаком соответствующей степени и ниже. Например:
Для регрессии с двумя признаками.
Линейная модель (полином степени 1):
\[h_b (x) = b_0 + b_1 x_1 + b_2 x_2\]Квадратичная модель (полином степени 2):
\[h_b (x) = b_0 + b_1 x + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2\]Кубическая модель (полином степени 3):
\[\hat{y} = h_b (x) = b_0 + b_1 x_1 + b_2 x_2 + \\ + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2 + \\ + b_6 x_1^3 + b_7 x_2^3 + b_7 x_1^2 x_2 + b_8 x_1 x_2^2\]При этом количество признаков и, соответственно, количество параметров растет экспоненциально с ростом степени полинома. Поэтому полиномиальные модели обычно очень затратные в обучении при больших степенях. Но полиномы высоких степеней более универсальны и могут аппроксимировать более сложные данные лучше и точнее.
Выводы:
- Данные в датасете не всегда располагаются так, что их хорошо может описывать линейная функция.
- Для описания нелинейных зависимостей нужна более сложная, нелинейная модель.
- Чтобы не изобретать алгоритм обучения заново, можно просто ввести в модель суррогатные признаки.
- Суррогатный признак - это новый признак, который считается из существующих атрибутов.
- Чаще всего используют полиномиальную регрессию - это когда в модель вводят полиномиальные признаки - степени существующих атрибутов.
- Обычно берут все комбинации факторов до какой-то определенной степени полинома.
- Полиномиальная регрессия может аппроксимировать любую функцию, нужно только подобрать степень полинома.
- Чем больше степень полиномиальной регрессии, тем она сложнее и универсальнее, но вычислительно сложнее (экспоненциально).
Полиномиальная классификация
Напомним, как выглядит функция модели:
Эта самая простая модель показывает себя хорошо даже и во многих реальных задачах. Особенно если в датасете собрано множестве признаков, есть неплохой шанс на появление линейных связей в данных. Во всяком случае, линейную модель стоит протестировать одной из первых.
Но зачастую мы имеем такие данные, которые просто не могут быть описаны линейной моделью. В таком случае, стоит строить более сложные модели. Мы уже говорили о полиномиальных моделях для задач регрессии. Но они с равным успехом могут применяться и для классификации. Рассмотрим, например, такой набор данных.
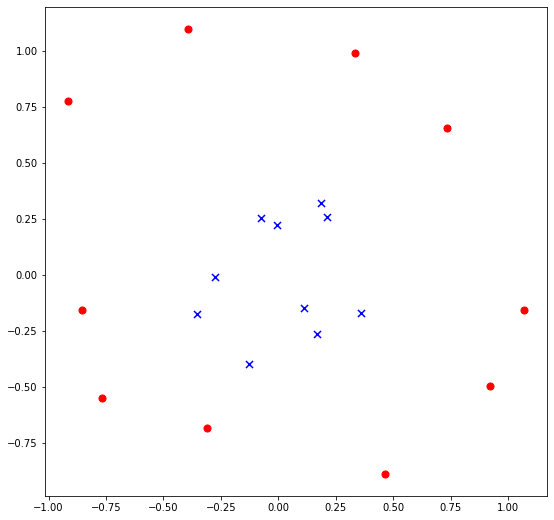
Здесь тоже очень четко прослеживается граница между двумя классами, то есть потенциальная граница принятия решения. Только очевидно, что она носит не линейный характер. Для того, чтобы построить такую границу нам можно взять более сложную функцию, содержащую признаки во второй степени (так как мы подозреваем, что граница принятия решений является кривой второго порядка). Например, возьмем такую функцию:
Конечно, когда в наборе данных больше двух признаков, такие простые графики не получится построить. Поэтому очень сложно заранее сказать, есть ли преобладающая линейная зависимость или данные описываются нелинейными моделями. Здесь мы рисуем эти графики, чтобы показать, как устроены и как работают модели. Они не используются для подбора моделей. Это вообще зачастую выбор “вслепую”.
Мы говорили, что полиномиальную модель можно рассматривать двумя способами - как модель более сложного класса и как добавление новых признаков к набору данных и, таким образом, переход в пространство боле высокой размерности. Рассмотрим простой пример. Выведем на печать матрицу признаков с графика выше:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
array([[-0.31, -0.68],
[ 0.36, -0.17],
[ 0.17, -0.26],
[-0.07, 0.26],
[-0.85, -0.16],
[-0.13, -0.4 ],
[ 0.11, -0.15],
[ 0.19, 0.32],
[-0.77, -0.55],
[-0.01, 0.22],
[ 0.73, 0.66],
[ 0.33, 0.99],
[ 0.21, 0.26],
[-0.39, 1.1 ],
[ 0.46, -0.89],
[ 1.07, -0.16],
[-0.35, -0.18],
[-0.92, 0.77],
[-0.27, -0.01],
[ 0.92, -0.5 ]])
Анализируя график можно заметить, что синие точки (положительный класс) сосредоточены ближе к началу координат, а красные - дальше от него. Расстояние от начала координат для каждой точки можно вычислить как сумму квадратов ее координат. Давайте добавим в матрицу третий столбец - еще один признак - сумму квадратов первых двух признаков:
1
X1 = np.append(X, (X[:, 0] ** 2 + X[:, 1] ** 2).reshape((-1, 1)), axis=1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
array([[-0.31, -0.68, 0.56],
[ 0.36, -0.17, 0.16],
[ 0.17, -0.26, 0.1 ],
[-0.07, 0.26, 0.07],
[-0.85, -0.16, 0.75],
[-0.13, -0.4 , 0.18],
[ 0.11, -0.15, 0.03],
[ 0.19, 0.32, 0.14],
[-0.77, -0.55, 0.89],
[-0.01, 0.22, 0.05],
[ 0.73, 0.66, 0.97],
[ 0.33, 0.99, 1.09],
[ 0.21, 0.26, 0.11],
[-0.39, 1.1 , 1.36],
[ 0.46, -0.89, 1. ],
[ 1.07, -0.16, 1.17],
[-0.35, -0.18, 0.16],
[-0.92, 0.77, 1.44],
[-0.27, -0.01, 0.08],
[ 0.92, -0.5 , 1.09]])
Целевую переменную мы, конечно, не трогаем. Давайте посмотрим на трехмерный график - расположение этих точек в пространстве более высокой размерности:
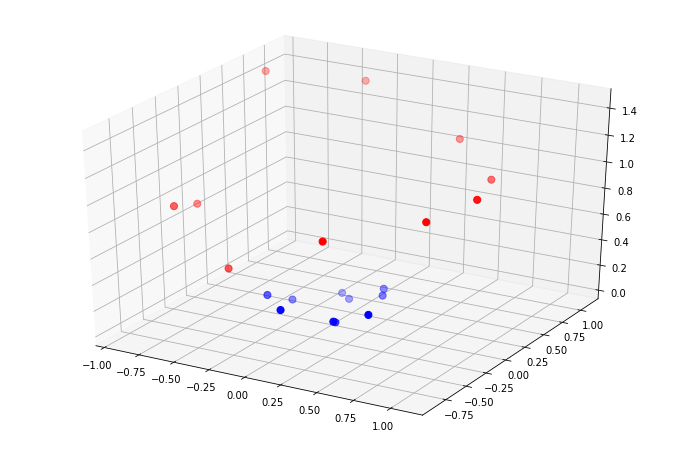
Мы видим, что за счет введения третьего признака набор данных стал очень даже линейно разделимым. Теперь синие точки располагаются ниже красных и их можно отделить плоскостью. В данном конкретном случае, плоскость будет горизонтальна, то есть при разделении мы будем использовать вообще только третий признак. В общем случае это не выполняется. Важно, что точки стали располагаться так, что их теперь можно будет разделить, например, вот так:
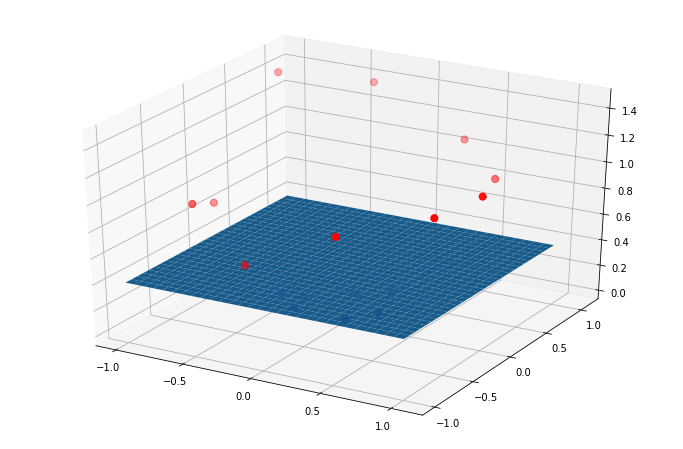
То есть после добавления полиномиального признака мы используем обычную линейную модель, но в надпространстве. Откуда же берутся нелинейные границы принятия решений? Это происходит когда мы пытаемся изобразить эту границу в изначальном двумерном пространстве. Ведь изначальная плоскость двумерного графика в этом трехмерном пространстве будет представляться поверхностью второго порядка вот так:
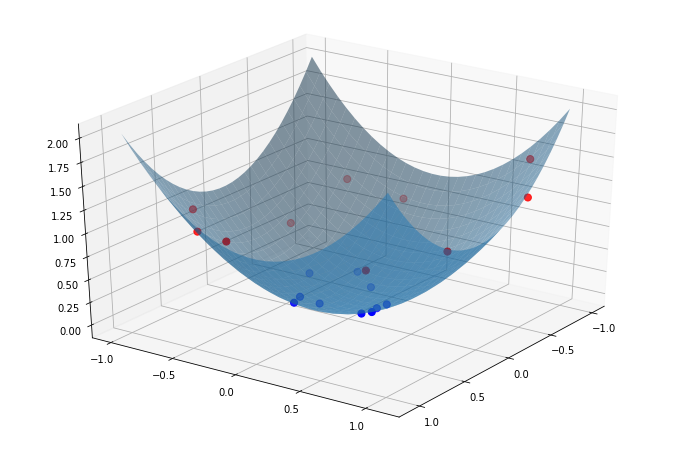
Пересечение этой поверхности с нашей плоскостью принятия решения как раз и формирует границу, которую модель строит на двумерном графике. Получается кривая второго порядка. Она может выглядеть примерно так:
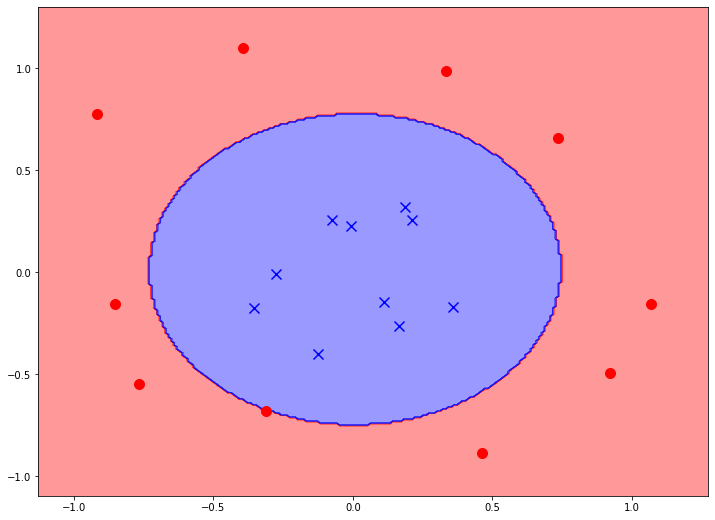
На этом примере мы, кстати, можем видеть, почему так труден анализ многомерных данных. Наш изначальный двумерный график с точками по сути своей представляет собой проекцию трехмерного графика на горизонтальную плоскость. Когда мы изображаем два каких-то признака из множества, мы всегда берем проекцию. Так вот, в трехмерном графике абсолютно очевидна линейная разделимость данных. Однако, когда мы анализируем проекцию, данные становятся как бы “вперемешку”. Поэтому по проекции нельзя судить о наличии или отсутствии структуры в данных.
На практике мы не можем знать, какой именно искусственный признак даст нам разделимость выборки в пространстве более высокой размерности. Поэтому обычно добавляют все возможные комбинации всех признаков до определенной степени полинома. В данном случае, для получения полинома второй степени нам нужно было еще добавить признаки $x_1^2$ и $x_2^2$. Они бы не очень влияли на расположение границы принятия решений, но линейные модели могут справится с “лишними” признаками в данных - коэффициенты при них будут просто близкими к нулю.
Но в общем случае, могут использоваться все признаки в полиноме. Если у нас два изначальных атрибута и мы строим полином второй степени, то у нас получится пять признаков в модели - $x_1, x_2, x_1^2, x_2^2, x_x x_2$. Тогда граница принятия решений может быть любой кривой второго порядка. А может быть и так:
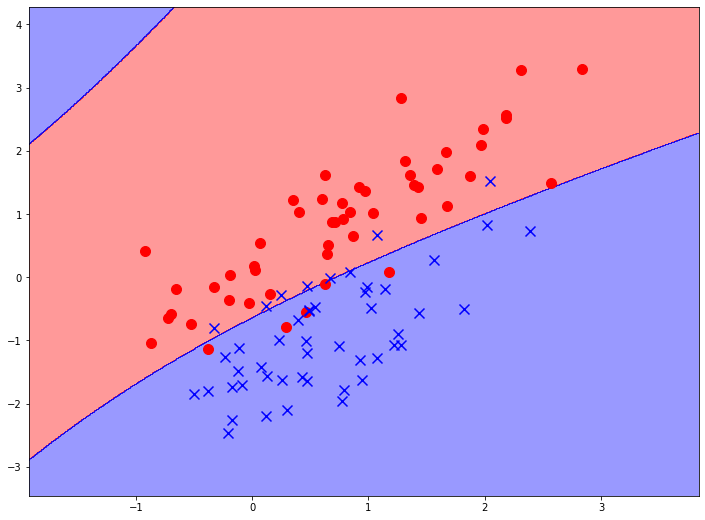
Ведь граница принятия решения - это по сути область пересечения гиперплоскости с поверхностью второго порядка. Это пересечение может иметь и более сложную форму.
Конечно, при работе с библиотечными функциями не придется руками перебирать все возможные полиномиальные комбинации. Поэтому достаточно легко можно построить полиномиальную классификацию, например, 10-го порядка:
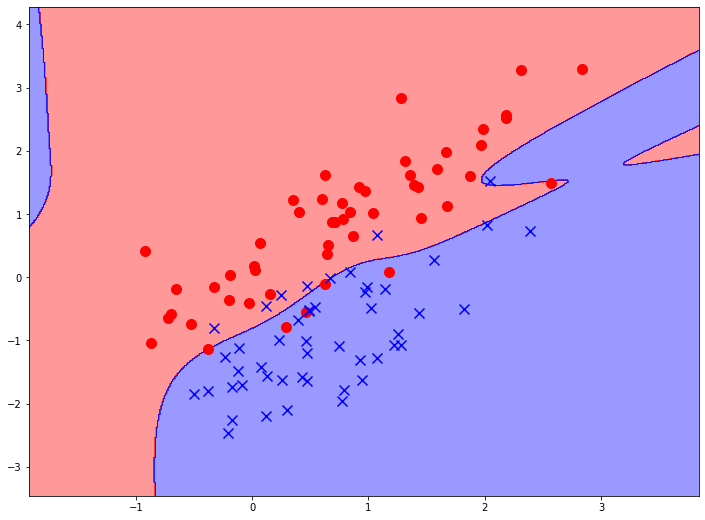
Она уже выглядит гораздо более сложной. За счет того, что она содержит гораздо больше признаков, она более вариабельна, и поэтому способна улавливать более сложные зависимости в данных и строить более сложные границы принятия решений.
Естественно, если мы представляем полиномиальные модели как модификацию исходного набора данных, а именно - добавление к нему новых признаков, то ничего не мешает применять этот пример как для регрессионных, так и для классификационных задач. Ниже вы видите пример полиномиальной модели регрессии со степенью полинома 2:
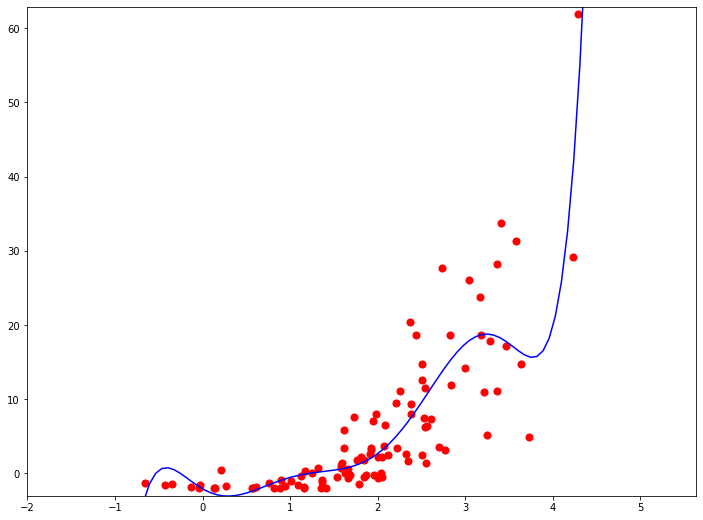
А на следующем графике - степень выросла до 7.Обратите внимание, насколько более сложной стала функция модели. Но в данном конкретном примере она все равно далека от того, чтобы пройти точно через все точки.
Здесь и далее мы уже будем употреблять термины “атрибут” и “признак” более точно. Раньше для нас это были синонимы. Так и есть при рассмотрении линейных моделей. Но, срого говоря, атрибут - это характеристика объекта реального мира. Оно зафиксировано в наборе данных и каждый атрибут обладает определенным смыслом в предметной области. Признак - это вектор, который подается на вход модели машинного обучения. Мы можем использовать как признаки сами атрибуты. Можем создавать новые признаки на основе существующих атрибутов. Можем удалять атрибуты из данных, так что они не становятся признаками. А можем модифицировать атрибут (например, нормировать его) и он превратится в другой признак.
Полиномиальные модели как для регрессии, так и для классификации - это универсальные аппроксиматоры. Ведь полиномом достаточно большой степени можно приблизить любую функцию. Этим, кстати и занимаются ряды Тейлора в математическом анализе. Поэтому с помощью полиномиальных моделей мы может решать задачи любой сложности. Однако, при высоких степенях полиномиальные модели могут быть не очень эффективны. Ведь количество признаков экспоненциально растет при увеличении степени. Если у нас изначально было два атрибута, то для второй степени получится, как мы уже считали, пять признаков, для третьей - 11, а для четвертой - уже 21. Но если изначально у нас было больше атрибутов, например, 10, то все еще хуже. Для второй степени понадобится 55 признаков, а для третьей - больше 500. В целом количество признаков растет экспоненциально. Так что если у вас изначально многопризнаков или задача очень сложная, то полиномиальные модели будут работать очень медленно.
Выводы:
- Добавление полиномиальных признаков возможно как к регрессионным, так и к классификационным моделям.
- Полиномиальная регрессия позволяет охватывать нелинейные зависимости атрибутов и целевой переменной.
- Полиномиальная классификация позволяет очерчивать нелинейные границы принятия решений.
- Здесь и далее: атрибуты - характеристики объектов, данные в датасете; признаки - компоненты вектора, подающегося на вход модели машинного обучения.
- Полиномиальные модели универсальны, но очень дороги при высоких порядках полинома.
Метод опорных векторов
Вернемся на время к случаю линейно разделимых данных для задач классификации. Как мы знаем, для проведения классификации таких данных достаточно линейной модели. В случае линейно разделимых данных логистическая регрессия ищет какую-нибудь разделяющую гиперплоскость. Главное условие - чтобы точки разных классов оказались по разные стороны этой границы. На графике мы видим пример:

Очевидно, что в случае такого расположения точек данных можно провести несколько разделяющих прямых. Каждая их них соответствует модели классификации. И у каждой из них будет ошибка, почти равная нулю, ведь они все разделяют данные идеально. Но при взгляде на такой график любому становится очевидно, что одна из разделяющих линий предпочтительнее других. Как вы думаете, какая?
Большинство людей ответит, что вторая. Однако, сложнее объяснить, почему мы так думаем. С формальной точки зрения, между ними нет никакой разницы, ведь они все дают нулевую ошибку. Но первая и третья линии проходят подозрительно близко к точкам одной из групп. Почему мы интуитивно считаем, что это плохо.
Следует всегда помнить, что задача модели машинного обучение - не предсказание правильного ответа для обучающей выборки. Мы его и так знаем. Но на примере этой выборки модель должна выявить зависимости в данных, которые позволят классифицировать объекты новые, которых модель еще не видела. Это свойство моделей называется обобщающей способностью. Об этом мы еще поговорим дальше.
Возьмем, например, первую линию. Она прекрасно разделяет те точки, которые мы видим. Но если заставить эту модель классифицировать точку, которая отстоит немного влево от основной группы синих точек, она может дать сбой. Пока мы просто предполагаем такой случай. Позже мы научимся формально его описывать и исключать.
Поэтому чем ближе граница принятия решений к середине между группами точек, принадлежащих разным классам, чем дальше она от самих этих групп, тем надежнее выглядят предсказания данной модели. Это не имеет непосредственного отношения к измерению эффективности моделей, но придает нам уверенность в результативности и обобщающей способности модели.
Это расстояние между границей принятия решения и крайними точками выборки, принадлежащими разным классам называется зазором между границей и точками. Можно поставить задачу нахождения разделяющей гиперплоскости максимального зазора. То есть из всех границ принятия решений мы будем выбирать лучшую, ориентируясь не только на значение логарифмической функции ошибки, но и на величину зазора.
Опять, как и раньше мы начнем с модификации уже известного нам алгоритма логистической регрессии. А модифицировать его мы будем так, чтобы он максимизировал зазор между границей и точками. Для этого мы модифицируем функцию ошибки таким образом, чтобы
Раньше, в классической модели логистической регрессии, ошибка плавно уменьшалась при стремлении значения линейной комбинации (до передачи в логистическую функцию) в правильную бесконечность. То есть, если реальное значение $y$ у данной точки - 0 (правый график), то есть точка принадлежит отрицательному классу, то чем меньше значение $z$, тем ближе ошибка в данной точке к нулю. При росте $z$ - ошибка неограниченно растет до бесконечности. Если же истинное значение $y = 1$ (левый график), то есть данная точка принадлежит положительному классу, то все наоборот - чем больше $z$, тем ближе ошибка к нулю. Помните, что формулировка функции ошибки - это наша цель оптимизации. То есть, используя именно эту функцию ошибки мы “заставляем” модель принимать правильные значения. И, что важнее, “штрафуем” ошибки. Причем, величина штрафа плавно увеличивается при увеличении степени ошибки.
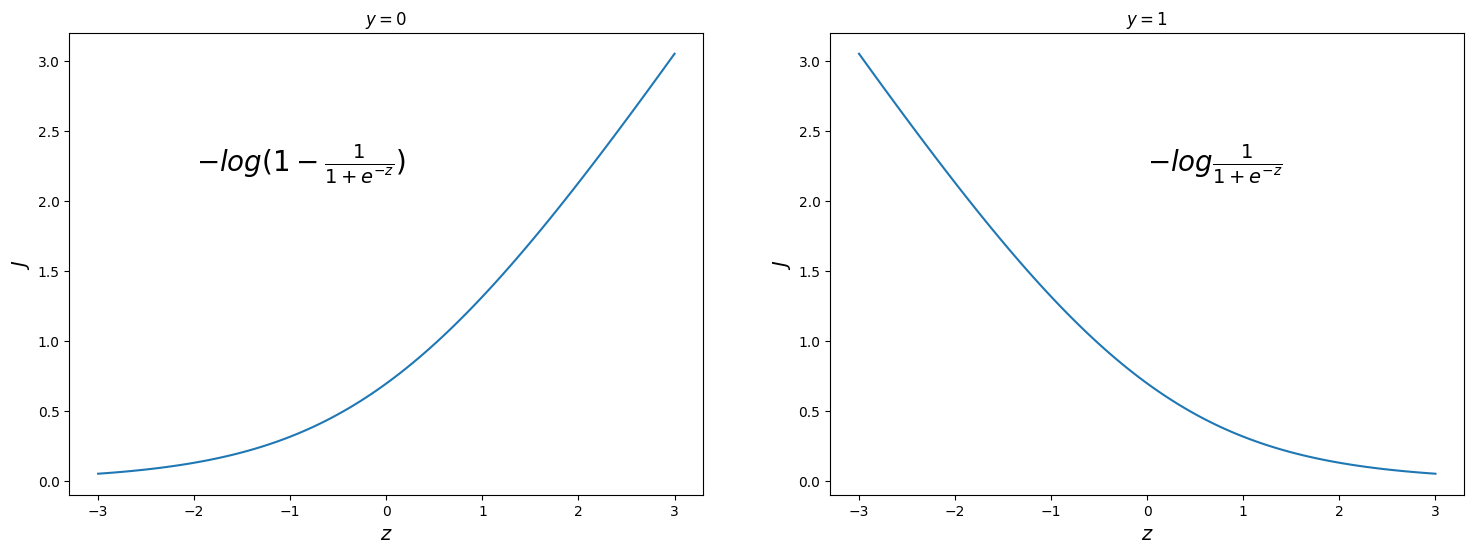
Однако, если мы хотим принять во внимание зазор, то мы должны усилить формулировку функции ошибки. В частности, мы вообще не будем штрафовать значения $z$, которые дают предсказания, близкие к истинному значению целевой переменной. А ошибочные значения будут штрафоваться пропорционально их отклонению от “идеального” значения.
Опять, рассмотрим два случая в каждой точке обучающей выборки. Допустим, истинное значение - 0 (правый график). Тогда при значениях $z <= -1$ мы вообще не штрафуем модель. То есть, говорим, что ошибка в этой точке равна нулю. Не приближается, а именно точно равна. Если же $z > -1$, то ошибка линейно возрастает пропорционально удалению от этой точки. Если же $y = 1$ (левый график) - то мы не штрафуем значения $z >= 1$. а остальные - так же пропорционально удалению.
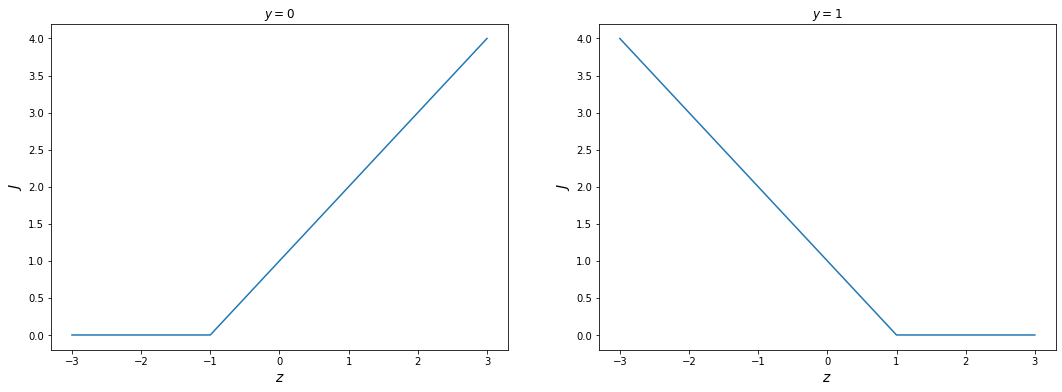
Обратите внимание, что такая ошибка подразумевает, что некоторый диапазон значений $z$ штрафуется в любом случае. Но в каждом случае, есть некий порог, при преодолении которого ошибка обращается в ноль. И так же, как и в классической модели логистической регрессии, полная ошибка вычисляется как сумма ошибок в каждой точке. Такая ошибка позволяет максимизировать зазор между разделяющей гиперплоскостью и крайними точками выборки. Именно за счет такого усиления формы ошибки. А эти крайние точки и называются опорными векторами.
Однако, есть одна проблема практического свойства. Как вы могли заметить, такая функция ошибки не везде дифференцируема. Поэтому для реализации такой модели мы прибегаем к трюку. Можно заметить, что положение нашей границы принятия решений определяется исключительно положением этих крайних точек, то есть опорных векторов.
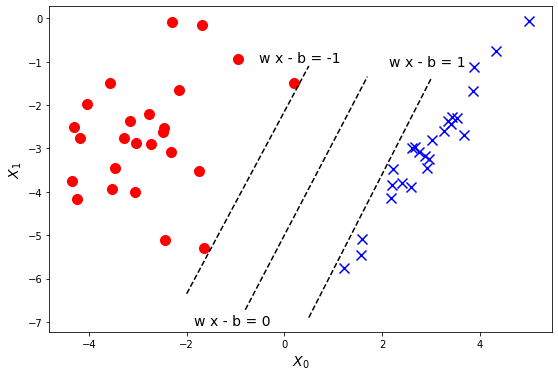
На данном графике показаны опорные вектора (точки), которые определяют “полосу” нейтральной зоны. И граница принятия решения должна располагаться ровно посередине этой полосы. Причем, в зависимости от взаимного положения точек и их принадлежности разным классам, опорных векторов может быть разное количество. Но их будет как минимум два - по одной точке от каждого класса.
Поэтому вместо того, чтобы вычислять функцию ошибки, нам нужно найти в обучающей выборке те самые опорные вектора. В двумерной задаче это может быть сделано достаточно просто - мы можем найти такие точки выборки, которые имеют наименьшее расстояние от точек противоположного класса. Например, рассмотрим такую выборку:
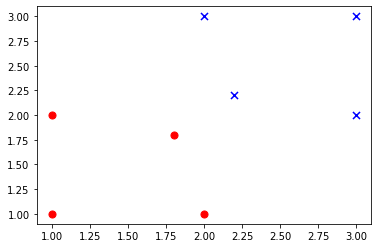
Эта выборка соответствует такому расположению точек:
1
2
3
4
5
6
7
8
9
10
11
X = np.array([
[1, 2],
[2, 1],
[1, 1],
[2, 3],
[3, 2],
[3, 3],
[1.8, 1.8],
[2.2, 2.2]
])
Y = np.array([0, 0, 0, 1, 1, 1, 0, 1])
Мы можем найти матрицу расстояний от каждой точки до каждой другой:
1
X1 = np.array([[distance(p1, p2) for p1 in X] for p2 in X])
1
2
3
4
5
6
7
8
[[0. , 2. , 1. , 2. , 4. , 5. , 0.68, 1.48],
[2. , 0. , 1. , 4. , 2. , 5. , 0.68, 1.48],
[1. , 1. , 0. , 5. , 5. , 8. , 1.28, 2.88],
[2. , 4. , 5. , 0. , 2. , 1. , 1.48, 0.68],
[4. , 2. , 5. , 2. , 0. , 1. , 1.48, 0.68],
[5. , 5. , 8. , 1. , 1. , 0. , 2.88, 1.28],
[0.68, 0.68, 1.28, 1.48, 1.48, 2.88, 0. , 0.32],
[1.48, 1.48, 2.88, 0.68, 0.68, 1.28, 0.32, 0. ]]
Конечно, на главной диагонали будут нули. Но нам нужно выбрать из этой матрицы минимально значение между двумя точками, принадлежащими разным классам. Такое значение всегда будет. Поэтому хотя бы два опорных вектора будут всегда присутствовать в любой задаче. В нашем случае это расстояние между последней и предпоследней точками, а именно значение 0,32. Значит эти две точки и будут опорными векторами в данной обучающей выборке.
Рассмотрим другой пример:
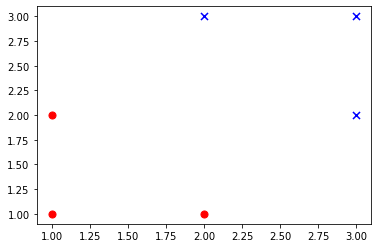
В этой выборке мы удалили две центральные точки. Где же будут опорные вектора? Так же рассмотрим матрицу взаимных расстояний точек:
1
2
3
4
5
6
[[0, 2, 1, 2, 4, 5],
[2, 0, 1, 4, 2, 5],
[1, 1, 0, 5, 5, 8],
[2, 4, 5, 0, 2, 1],
[4, 2, 5, 2, 0, 1],
[5, 5, 8, 1, 1, 0]]
Учитывая, что нам нужны расстояния между точками разных классов, находим, что между точками 0-3 и 4-1 минимальное расстояние - 2. Можете проверить самостоятельно - меньшие расстояния в матрице только между точками одного класса. Это, вообще, типичный случай, ведь расстояние между точками - это некоторая мера их сходства. А схожие точки чаще принадлежат одному классу, чем разным.
Получается, что в этой выборке сразу четыре опорных вектора? Да, и такое бывает. Вообще, опорных векторов может быть любое количество, это зависит от взаимного расположения точек в пространстве.
Важно то, что эти опорные вектора однозначно определяют положение границы принятия решений. Если изменить положение хотя бы одного опорного вектора - то положение границы изменится. А если изменить положение точки, которая не является опорным вектором, то граница останется на том же месте. Это позволяет при классификации использовать положение всего нескольких точек выборки.
Следует заметить, что при изменении положения неопорной точки она сама может стать опорной, если приблизится к границе принятия решений. Поэтому, конечно, при изменении данных модель следует пересчитать заново.
Однако, при размерности точек, большей двух, нахождение опорных векторов уже не так тривиально. И эту задачу решают при помощи численной оптимизации. Ставится эта задача так. Граница принятия решения определяется как область точек, скалярное произведение которых с заданным вектором постоянна. Этот заданный вектор вычисляется как линейная комбинация векторов признаков с параметрами. Или, другими словами, взвешенное среднее векторов признаков, где веса выступают параметрами. Вектор параметров в таком случае выступает как нормальный вектор к разделяющей гиперплоскости.
Причем этот вектор (его обычно обозначают $w$ и он в наших обычных терминах будет состоять из таких компонент: $\vec{b} = {b_1, b_2, …, b_n}$) не обязательно единичной длины, как обычно в линейной алгебре. Ширина зазора между гиперплоскостью и точками однозначно определяется как величина, обратная к длине нормального вектора. Поэтому задача сводится к минимизации длины нормального вектора, при сохранении условия, что все точки классифицируются правильно.
Последнее требование можно смягчить, ведь на практике не все выборки являются линейно разделимыми. Поэтому классификатор может допускать некоторую степень неправильных классификаций. Таким образом оптимизироваться будет некоторая величина, состоящая и из длины нормального вектора и из суммарной ошибки классификации. Эта задача решается методом поиска седловой точки функции Лагранжа, рассмотрение которого выходит за рамки данного пособия.
Важно то, что представленная таким образом задача приводит к нахождению разделяющей гиперплоскости максимального зазора. На графике вы можете видеть результат применения данного метода к уже использованным нами данным:
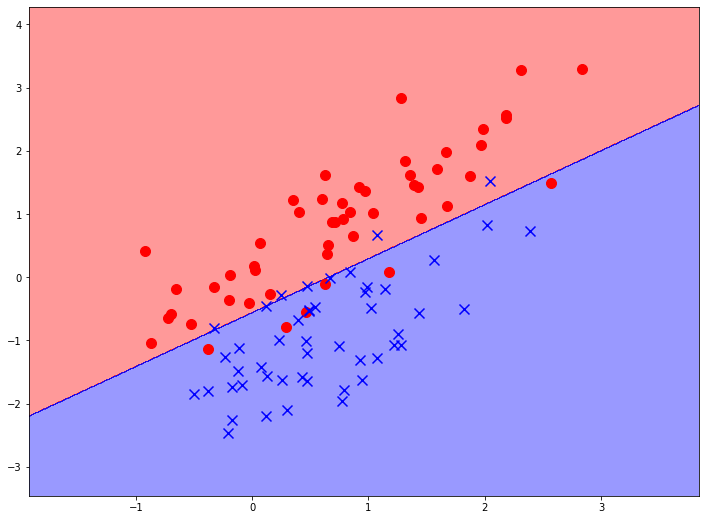
Можно видеть, что результат достаточно близок к результату применения линейной регрессии. Вообще, метод опорных векторов в такой формулировке в чем-то аналогичен линейным методам. Он дает линейную границу принятия решений. Но так же может использоваться и для нахождения линейной регрессии:
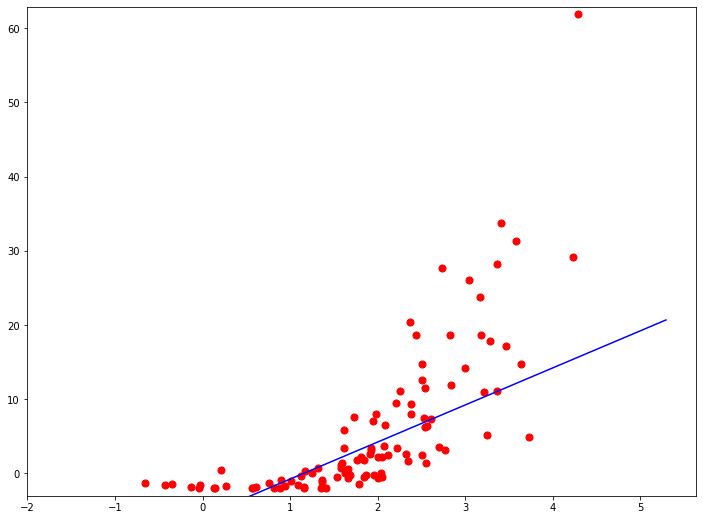
В таком виде метод опорных векторов просуществовал с начала 60-х до начала 90-х годов. В это время исследователи догадались, что такая постановка задачи позволяет совершить один трюк, который сильно расширяет применение и вариативность метода опорных векторов. Этот трюк может быть применен для решения линейно неразделимых задач, то есть для построения нелинейных границ принятия решений. Давайте для примера рассмотрим двумерную выборку, точки которой располагаются на плоскости примерно так:
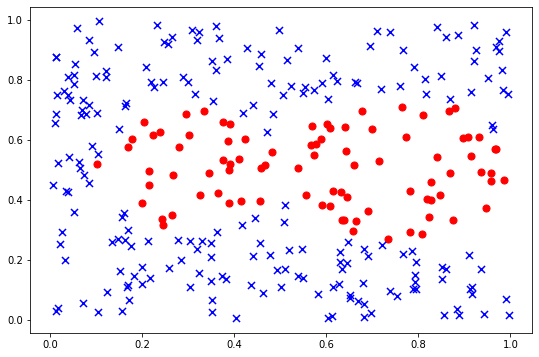
Очевидно, что данные могут быть разделены некоторой не очень сложной кривой. Но конкретный вид этой кривой достаточно сложно найти. В полиномиальной модели мы просто добавляем полиномиальные признаки “вслепую”, используя все комбинации. Это очень неэффективно. Метод опорных векторов тоже позволяет перейти в пространство более высоких размерностей, но без использования “полного перебора” всех комбинаций до заданной степени полинома, а используя так называемый “ядерные функции”.
Давайте зададимся вопросом. Можно ли более эффективно задать признаки для данной выборки точек? Глядя на график становится очевидно, что точки положительного класса (синие) расположены двумя пересекающимися примерно круглыми группами. А точки отрицательного класса (красные) расположены вне этих круглых кластеров. Это наводит на мысль, что в качестве признаков в модели мы можем использовать вообще не само расположение этих точек. Например, что если признаком сделать расстояние от данной точки до выбранных “центров кластеров”? Тогда данная проблема станет линейно разделимой. Хотя граница принятия решения будет сложной формы.
Математически доказано, что такая постановка проблемы эквивалента использованию в методе опорного вектора вместо скалярного произведения другой функции - радиально-базисной. Это и называется “ядерной функцией” или “функцией ядра” метода опорных векторов. То есть мы не изменяем саму задачу, но по-другому определяем саму разделяющую гиперплоскость. В данном случае - разделяющей гиперплоскостью будем считать множество точек $x$, которые удовлетворяют следующему равенству:
где $x_i$ - опорные вектора (в нашем примере - центры кластеров), $\alpha_i$ - их веса, а $k$ - ядерная функция (некоторая мера расстояния или сходства между точками).
Если правильно подобрать опорные вектора, то наша выборка станет абсолютно линейно разделимой. Как и раньше мы можем думать об этом преобразовании, как о добавлении новых признаков в модель (в нашем случае происходит даже замена признаков, потому что изначальные атрибуты не используются), либо как формирование нелинейной границы принятия решений в исходном пространстве.
На практике встает вопрос: а как выбирать эти самые опорные вектора? В простых случаях, как на графике выше, мы можем их проставить вручную, но это очень не универсальный способ. Конечно, нужен метод, который находит их автоматически. И вот здесь как раз используется тот же самый математический аппарат, что и в описанном выше линейном случае. Мы не находим и не задаем опорные вектора сами, мы используем все точки обучающей выборки и оптимизируем их веса таким образом, чтобы он был тем выше, чем “больше” точка является опорной.
Когда мы рассматривали простой линейный случай, точки выборки у нас могли быть либо опорными, либо нет. Но на самом деле все немного сложнее. Ведь любая гиперплоскость однозначно определяется всего одним вектором - нормальным. А этот нормальный вектор “составляется” как взвешенная сумма векторов, соответствующих всем точкам обучающей выборки. Другими словами, в качестве опорных векторов для начала берут сами точки обучающей выборки. А затем, в процессе обучения, быстро становится понятно, что не все точки “одинаково полезны”. У таких не полезных точек вес будет равен или очень близок к нулю. Если же точка близка к центру кластера, то ее вес будет ненулевым.
На самом деле, конечно, гиперплоскость задается не только нормальным вектором, но еще и некоторым числом. Это число характеризует расстояние плоскости от центра координат. Это число - это свободный коэффициент $b_0$. Если помните, вектор $w$ в методе опорных векторов как раз задавался без него. Этот параметр $b_0$ в совокупности с другими параметрами однозначно задает разделяющую гиперплоскость. Здесь присутствует некоторая информационная избыточность, ведь, например, в двух измерениях, разделяющая прямая задается уравнением $b_0 + b_1 x_1 + b_2 x_2 = 0$. Это уравнение имеет 3 параметра, но всего 2 степени свободы. Ведь его можно свободно умножить на любое ненулевое число.
Для полного определения нашей нелинейной модели на опорных векторах, нужно лишь охарактеризовать саму “ядерную функцию”. Мы уже сказали, что в качестве функции ядра может применяться скалярное произведение векторов. Если мы зафиксируем некоторую точку (вектор) в пространстве, то постоянное скалярное произведение даст нам множество плоскостей, равноудаленных от данной точки. А для решения нашей второй, нелинейной задачи, нам нужна функция, которая даст окружность вокруг данной точки. Такая ядерная функция называется радиально-базисная и формулируется следующим образом:
Вид этой функции очень похож на нормальное распределение. Поэтому данная функция еще называется гауссовой. Относительно конкретной точки эта функция показывает некоторую меру сходства. которая убывает при росте евклидова расстояния от нее. Действительно, если мы посчитаем радиально-базисную функцию от двух совпадающих точек, мы получим 1. Если же точки будут бесконечно далеки друг от друга, то значение функции будет стремиться к нулю. В общем случае, эта функция ведет себя как распределение Гаусса, откуда и название.
Применение этой функции в методе опорных векторов означает, что мы строим разделяющую гиперплоскость, выглядящую как множество равноудаленных точек от некоторого средневзвешенного вектора в пространстве высокой размерности. Если мы спроецируем эту границу принятия решений в наше изначальное пространство, то оно будет выглядеть как некоторая кривая (в большинстве случаев замкнутая), похожая на эллипс, то есть кривую второго порядка, но более сложной формы. Сложность границы принятия решений в методе опорных векторов зависит не от нелинейности ядерной функции, а от того, сколько точек выборки метод примет за опорные.
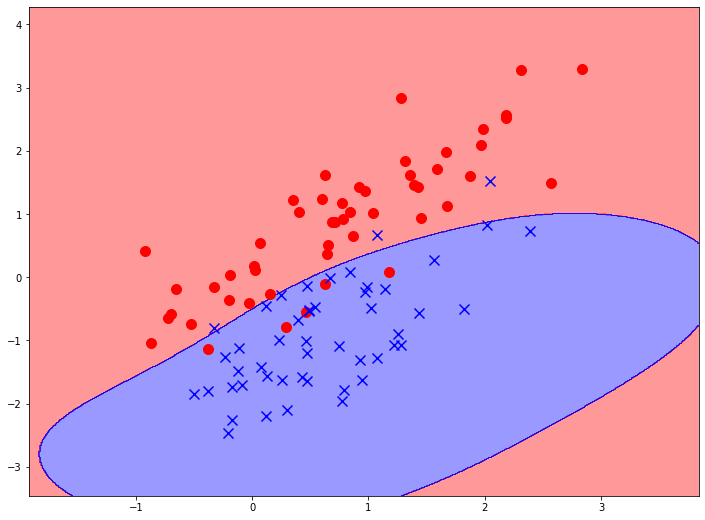
Метод опорных векторов с гауссовым ядром очень редко применяется для решения задач регрессии, так как обладает очень характерным поведением, которое вы можете видет на графике. Это поведение достаточно редко встречается в реальной жизни в данных, предполагающих регрессионные задачи.
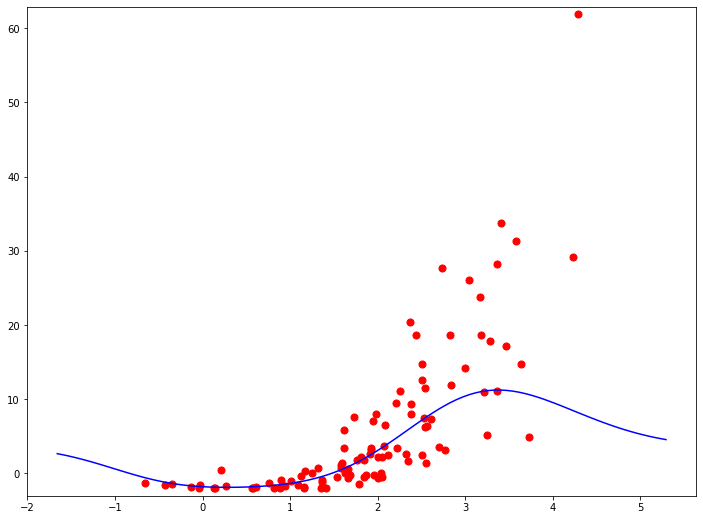
Так как метод опорных векторов не привязан к конкретной задаче - регрессии или классификации - в общем виде он обозначается SVM - support vectors machine. Если же мы говорим о его адаптации к задаче регрессии, то можно встретить аббревиатуру SVR - support vectors regressor, то есть регрессор на основе метода опорных векторов. И, соответственно, существует SVC - support vectors classifier, классификатор на опорных векторах.
Следует заметить, что описанный выше алгоритм линейной классификации при помощи метода опорных векторов, когда в качестве ядреной функции применяется скалярное произведение, называется метод опорных векторов с линейным ядром. Он же, по ряду причин, называется метод опорных векторов без ядра. Имейте это в виду, данная терминология может немного ввести в заблуждение.
В качестве функции расстояния можно брать разные метрики (они должны удовлетворять определенным условиям). С большим отрывом чаще всего применяются на практике линейное и гауссово ядро. А так как линейное ядро почти всегда аналогично применению обычной линейной регрессии, по умолчанию почти всегда применяется именно гауссово ядро. В библиотечных реализациях метода опорных векторов обычно есть возможность выбрать их нескольких уже готовых ядерных функций.
Наиболее распространенные ядерные функции:
- Линейное (SVM без ядра): $ (x \cdot x’) $
- Радиальная базисная функция: $ e^{-\gamma \mid x - x’|^2} $
- Полиномиальное: $ (x \cdot x’)^d $
- Полиномиальное смещенное: $ (x \cdot x’ + 1)^d $
- Сигмоида: $ tanh(k x \cdot x’ + c) $
Метод опорных векторов с разным типом ядер дает разный тип границы принятия решений. Например, ниже вы видите результат работы классификатора на опорных векторах с полиномиальным ядром. Полиномиальное ядро подразумевает, что предварительно надо задать еще и степень полинома. По умолчанию, и на графиках ниже используется третья степень.
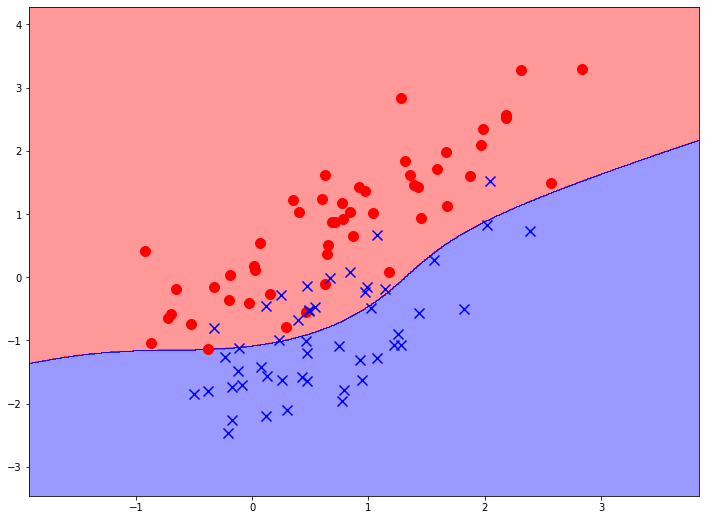
Такой же метод опорных векторов с полиномиальным ядром третьей степени, но уже для решения задачи регрессии. Можно заметить, что кривая несомненно сложнее, чем кривая третьего порядка. Ведь сложность границы принятия решения зависит от количества опорных векторов.
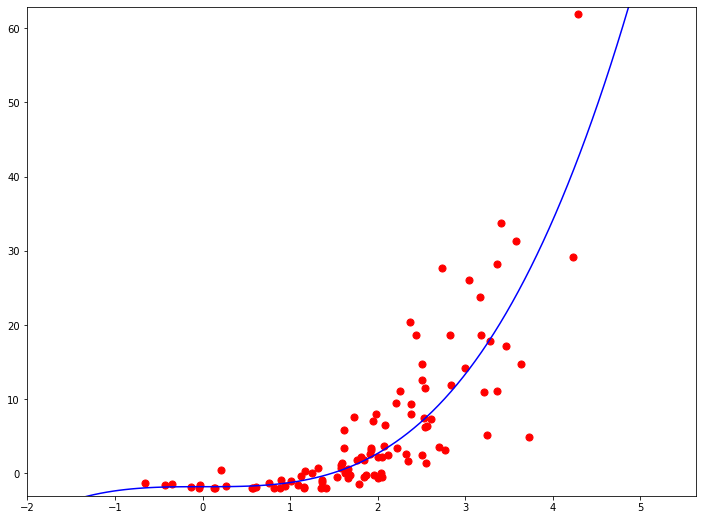
Метод опорных векторов имеет ряд преимуществ и недостатков по сравнению с линейными и полиномиальными моделями. Он, несомненно, более эффективен в построении нелинейных границ принятия решений, чем полиномиальные модели. Он более универсален, чем линейные. Но надо помнить, что в процессе нахождения опорных векторов в какой-то момент приходится оценивать расстояние между точками выборки. Поэтому данный метод может выполняться довольно медленно, если точек большое количество. Но с другой стороны, если в задаче количество точек сильно меньше, чем количество атрибутов, метод опорных векторов наоборот, может дать преимущество в скорости.
Но метод опорных векторов менее интерпретируем и понятен, чем линейные модели. Результат работы классификатора нельзя интерпретировать как вероятность принадлежности объект данному классу, как в линейных и полиномиальных моделях. А это затрудняет его использование в мультиклассовых задачах (то ест в таких, где объект может одновременно принадлежать нескольким классам) и в задачах нечеткой классификации.
Выводы:
- Метод опорных векторов находит оптимальную разделяющую гиперплоскость, а значит приводит к более уверенной классификации.
- SVM может реализовывать нелинейные модели за счет применения функций ядер.
- Метод опорных векторов может использоваться как для регрессии (SVR), так и для классификации (SVC).
- SVM эффективны, когда количество атрибутов больше количества объектов.
- SVM очень чувствителен к шуму, выбросам в данных.
- SVM не дают прямых оценок вероятности принадлежности.
Перцептрон
Перцептрон - это самый простой вид искусственных нейронных сетей. Вообще, подробное рассмотрение нейронных сетей выходит за рамки этого пособия, это отдельная и очень глубокая тема, требующая подробного изучения. Но именно перцептрон довольно часто используется наряду с другими классическими методами обучения с учителем. Поэтому здесь мы рассмотрим основные принципы работы перцептрона именно для решения относительно простых задач регрессии и классификации, без подробного рассмотрения техник глубокого обучения. Для того, чтобы познакомиться с работой нейронной сети, рассмотрим сначала принцип действия одного искусственного нейрона.
На минутку возвратимся к обычной логистической регрессии. Ее можно схематически изобразить, как прохождение сигнала (численной информации) по такой схеме:
Здесь есть несколько входов $x_i$ - на которые подаются значения соответствующих признаков. Затем каждое из этих значений умножается на соответствующий ему вес - $w_i$ (именно они подбираются в процессе обучения), затем они суммируются, а после этого эта взвешенная сумма подается на вход некоторой нелинейной функции (в случае логистической функции - сигмоидальной). Обратите внимание, что на схеме присутствует один постоянный вход, на который подается всегда значение 1 - это искусственный константный признак, который нужен для учета свободного слагаемого в взвешенной сумме.
Таким образом модель логистической регрессии представляется в виде некоторого объекта, у которого есть несколько входов, один выход и какие-то внутренние параметры:
Этот объект в определенном смысле похож на то, как функционирует биологическая клетка нервной системы - нейрон. Он тоже имеет несколько входов, на которые могут быть поданы электрические сигналы. Если сумма этих сигналов превышает некоторый порог, то активируется выходной сигнал нейрона. Поэтому такое представление модели называется моделью нейрона, а программа, которая его реализует - искусственным нейроном. Мы можем пользоваться этим нейроном, как моделью классификации. Для этого на его входы надо подать значения, соответствующие значениям признака классифицируемого объекта. Тогда на выходе мы получим некоторое значение, которое можно интерпретировать, как значение бинарной классификации.
В искусственном нейроне можно использовать разные функции активации. Исторически, чаще всего использовалась так называемая ступенчатая функция. Она принимает значение 0, если на вход ей подается значение меньше либо равно нулю, или 1, если подается положительное значение. Другими словами эта функция активирует нейрон, если значение взвешенной суммы входных сигналов больше какого-то значения. Причем, это пороговое значение может регулироваться свободным параметром $w_i$. Так, пороговая функция эмулирует поведение биологического нейрона.

Но для прикладного применения такая функция не обязательно оптимальна, и поэтому можно использовать другие. Например, как мы уже говорили, если взять логистическую функцию активации, то такой нейрон будет полностью аналогичен модели логистической регрессии. Но на практике часто используют так называемую функцию ReLU (rectified linear unit):
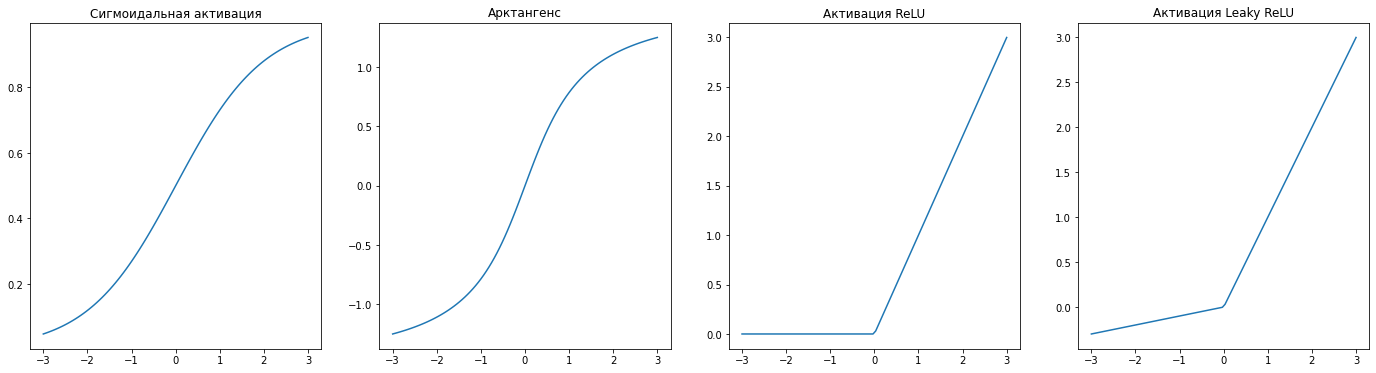
Но чем искусственный нейрон принципиально отличается от других моделей машинного обучения? Ключевых отличий два: возможность объединения в сети и алгоритм обучения. Сам по себе один нейрон представляет собой довольно простую модель, но именно такое представление позволяет очень просто объединять несколько нейронов - то есть соединять выход одного нейрона со входом другого, другими словами, подавать результат работы одного нейрона как значение признака другому. Такое становится возможным благодаря тому, что нейроны используют особую разновидность метода градиентного спуска для обучения - так называемый метод обратного распространения ошибки. Давайте на примере рассмотрим механизм обучения одного нейрона (однослойного перцептрона).
Создадим каркас нашего класса. В нем определим поля для хранения весов и смещения (в нейронных сетях они традиционно хранятся отдельно, хотя вы можете использовать и суррогатный признак), а также функцию активации (в данном случае используем пороговую функцию активации, она проще всего в вычислениях):
1
2
3
4
5
6
class Perceptron:
def __init__(self):
self.weights = None
self.bias = None
def activation_func(self, x):
return np.where(x>=0, 1, 0)
обратите внимание, что мы не инициализируем вектор весов, так как его размерность будет напрямую зависеть от количества признаков в данных.
Теперь определим функцию прямого распространения - то есть выполнение предсказания. Для этого используем переданную матрицу признаков (или вектор, если объект один), которую будем умножать на вектор весов. Конечно, предполагается, что вектор весов для этого должен быть инициализирован. Это мы будем делать в функции обучения. Так что перцептрон нужно сначала обучить, а уже потом применять. Прямое распространение сводится к вычислению линейной комбинации $z$, которую нужно пропустить через функцию активации:
1
2
3
def predict(self, X):
z = np.dot(X, self.weights) + self.bias
return self.activation_func(z)
Теперь можем приступить к реализации функции обучения. Здесь мы сначала инициализируем вектор весов случайными значениями. Обратите внимание, что нейронные сети нужно всегда инициализировать именно случайно. Для единственного нейрона это не критично, но многослойные нейронные сети должны иметь разные веса у нейронов на одном слое.
1
2
def fit(self, X, y):
self.weights = np.random.rand(X.shape[1])
Алгоритм обучения сводится к немного модифицированному градиентному спуску. В данном примере мы будем вычислять ошибку для каждого объекта обучающей выборки. Для градиентного спуска нам нужно сформировать функцию ошибки. Возьмем среднеквадратическое отклонение. В данном случае, так как используется всего один объект, это будет просто квадрат отклонения эмпирического значения от полученного:
В этой формуле $y$ - эмпирическое или истинное значение целевой функции. А $a^{(L)}$ - это значение функции активации нейрона на последнем слое. Другими словами это по сути и есть значение модели. В нейронных сетях так принято обозначать результат работы нейрона, и эти обозначения станут полезными, когда мы будем говорить о многослойных сетях. $L$ в данном случае - просто количество слоев.
При описании математики работы нейронных сетей часто приходится видеть обозначение номера слоя в виде верхнего индекса в скобках. Следует помнить, что это не возведение в степень, а именно индекс, то есть просто номер слоя, которому принадлежит данный параметр. Дело в том, что нижние индексы обычно заняты обозначением номера нейрона в слое. Также обратите внимание, что к слоям мы обращаемся с конца - сначала работаем с последним, затем с предпоследним и так далее. Это же алгоритм обратного распространения ошибки. Поэтому мы обозначаем слои не 1, 2, …, а через $L$ - количество слоев - $L$ - последний, $L-1$ - предпоследний и так далее.
Результат работы нейрона зависит от двух факторов - от значения весов $w^{(L)}_i$ (опять в обозначениях упоминается номер слоя, в данном случае - последний.) и от свободного парамера $b^{(L)}$. Для того, чтобы понять, как нам нужно поменять эти параметры, чтобы уменьшить ошибку, нужно вычислить градиент, или просто частную производную. Начнем с весов. Для упрощения расчетов сразу применим правило производной сложной функции:
Другими словами, зависимость значения ошибки от веса складывается из зависимости значения ошибки от значения нейрона, зависимость значения нейрона от линейной комбинации и значения линейной комбинации от веса. Давайте найдем эти частные производные по порядку:
Зависимость ошибки от значения нейрона следует из самой формулировки функции ошибки. Заметим только, что постоянный множитель можно в дальнейшем игнорировать, так как по методу градиентного спуска мы все равно будем домножать получившееся выражение на скорость обучения.
При расчете частной производной значения функции активации нейрона от линейной комбинации мы сталкиваемся в проблемой. Дело в том, что мы используем ступенчатую функцию активации, а ее производная равна нулю везде, где определена. По этой самой причине эта функция активации и не используется в многослойных нейронных сетях. Сейчас, без потери обучающей способности метода мы примем эту производную за единицу. Но имейте в виду, что в общем случае так делать нельзя, это математический трюк только для однослойного перцептрона и только для этой функции активации.
Частная производная линейной комбинации по весу равна входному значению. В данном случае - это сами атрибуты датасета, которые подаются на вход нашему нейрону:
Таким образом мы получаем правило для изменения значения весов нейрона:
Теперь проделаем те же манипуляции для свободного коэффициента. Так же используем правило производной сложной функции и разложим ее на аналогичные составляющие:
Здесь все полностью аналогично за исключением последнего множителя:
Здесь все еще проще - так как коэффициент свободный, производная по нему равна единице:
Таким образом аналогично обновляем значение свободного коэффициента:
Вот как это выглядит в виде программного кода:
1
2
3
4
5
6
7
8
def fit(self, X, y):
self.weights = np.random.rand(X.shape[1])
# for _ in range(1000):
for idx, x_i in enumerate(X):
y_pred = self.predict(x_i)
update = 0.01 * (y[idx] - y_pred)
self.weights += update * x_i
self.bias += update
Теперь можно использовать данную модель и обучить ее на каких-нибудь данных:
1
2
3
4
p = Perceptron()
p.fit(X, Y)
y_pred = p.predict(X)
accuracy_score(Y, y_pred)
Если запустить этот код, можно убедиться, что модель работает, но результат предсказания не очень хороший. Дело в том, что на мы по сути делаем только один шаг градиентного спуска. Для полноценного обучения модели нужно повторить процесс подстраивания параметров много раз, аналогично с тем, как мы поступали для линейной регрессии. Вот как выглядит итоговый код:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Perceptron:
def __init__(self):
self.weights = None
self.bias = 0
def fit(self, X, y):
self.weights = np.random.rand(X.shape[1])
for _ in range(1000):
for idx, x_i in enumerate(X):
y_pred = self.predict(x_i)
update = 0.01 * (y[idx] - y_pred)
self.weights += update * x_i
self.bias += update
def predict(self, X):
z = np.dot(X, self.weights) + self.bias
return self.activation_func(z)
def activation_func(self, x):
return np.where(x>=0, 1, 0)
Теперь поговорим про вторую главную особенность искусственных нейронов, из-за которой они стали очень популярны - способность объединяться в нейронные сети. А зачем вообще объединять нейроны в сеть? Как мы уже говорили ранее, для более эффективного моделирования к атрибутам можно добавлять искусственные, суррогатные признаки. Как в модели полиномиальной регрессии, когда добавление, например, признака $x_1^2$ может сделать классификацию значительно проще. Но на практике очень сложно заранее предугадать, какие именно суррогатные признаки будут полезны.Может быть, в модель стоит добавить признак $x_1 + x_2$? Или $3x_1 - 4x_3^2$? Это называется задача извлечения признаков. Ее можно решать в ручном режиме, когда аналитик сам создает суррогатные признаки исходя из интерпретации предметной области, постановки задачи и смысла имеющихся атрибутов. Но вообще, хотелось бы, чтобы эта задача решалась автоматически. Давайте представим уже известный нам перцептрон, но мы хотим, чтобы на его вход подавались не существующие атрибуты, а подобранные оптимальные признаки:
Этого можно добиться, подставив вместо каждого входа еще по одному нейрону, каждый из которых получает на вход атрибуты и выдает результат. Такая модель называется многослойным перцептроном - это простейшая нейронная сеть, в которой есть три слоя: входной слой, на котором подаются значения имеющихся в датасете атрибутов; выходной слой, нейрон на котором выдает результат классификации; и скрытый слой, на котором какое-то количество нейронов преобразуют атрибуты в признаки:
Почему такая модель будет подбирать оптимальные признаки? Дело в алгоритме обучения нейронной сети. Давайте подумаем, сколько параметров будет у такой модели? Она состоит из четырех нейронов, у каждого из которых по три входа. Три входа - значит четыре внутренних параметра (помните, что один параметр является свободным, в нейронных сетях он обычно называется bias или нейрон смещения). Итого получается 16 параметров. И они обучаются все вместе таким образом, чтобы при работе этой сети на обучающей выборке ее ответы как можно больше совпадали с имеющимися. То есть алгоритм обучения нейронных сетей подбирает оптимальное значение всех параметров сети для наилучших предсказаний. Веса последнего нейрона подбираются такие, чтобы из признаков получать нужные значения, а нейронов на скрытом слое - так, чтобы из атрибутов получать наилучшие линейные комбинации, которые после нелинейного преобразования (функции активации) давали наилучшие для предсказания признаки.
Соединять нейроны можно по-разному, в разном порядке, с обратными связями, циклами, используя нейроны разных типов, разные функции активации. Схема соединения нейронов называется архитектурой нейронной сети. Нейронные сети - это попытка алгоритмической имитации деятельности головного мозга человека. Существует большое количество шаблонов архитектуры нейросетей. Но самая простая - это перцептрон, который мы и рассматривали выше. Это сеть прямого распространения, то есть в ней сигнал идет строго в одном направлении - от входа к выходу, без соединений в обратную сторону. И нейроны в нем организуются в слои. Причем эти слои являются полносвязными, то есть все нейроны одного слоя соединены со всеми нейронами следующего слоя.
Как мы говорили ранее, нейронные сети используют специальный вариант алгоритма градиентного спуска для подбора своих параметров. Зачем же изобретать новый алгоритм обучения? Делов именно в том, что нейронные сети могут быть многослойными. И алгоритм обучения должен легко подстраиваться под любое количество слоев и нейронов в нем. Поэтому не очень удобно рассматривать множество всех параметров нейронной сети как один плоский вектор. Давайте рассмотрим чуть подробнее, как работает алгоритм обучения нейронных сетей - алгоритм обратного распространения ошибки.
В многослойной сети значение каждого нейрона зависит от трех факторов - его входных весов, веса нейрона смещения (другими словами, свободного коэффициента) и значения нейронов на предыдущем слое. Функция ошибки формулируется точно так же, как и в предыдущем примере с одним слоем. Зависимость функции ошибки от этих трех факторов выражаются частными производными. Производную функции ошибки о свободного коэффициента $b^{(L)}$ мы уже рассматривали, она не меняется. Производная ошибки от веса вычисляется аналогично, но в отличии от однослойного перцептрона, вес умножается не на значение атрибута, а на значение нейрона на предыдущем слое, поэтому:
А вот зависимость значения текущего нейрона от значения нейронов на предыдущем слое мы еще не анализировали. Принцип здесь тот же самый, раскладываем эту производную по правилу сложной функции:
Два первых множителя здесь полностью аналогичны другим факторам:
А вот зависимость линейной комбинации от значения предыдущего нейрона выражается просто коэффициентом при этом значении - то есть весом данного входа в текущем нейроне:
Таким образом мы получаем значение, на которое надо изменить значение нейрона на предыдущем слое, чтобы уменьшить функцию ошибки:
Но эта ситуация аналогична тому что мы рассматривали изначально - есть текущее значение нейрона, есть его отклонение от нужного значения. Только теперь мы должны изменить значение другого нейрона, расположенного на предыдущем слое. А это значение, в свою очередь, зависит от его весов, свободного параметра и значения нейронов на еще более предыдущем слое. То есть анализируя, насколько нам нужно изменить параметры нейрона на текущем слое, мы получили информацию, насколько нам нужно изменить значение нейронов на предыдущем слое. То есть ошибка (отклонение) как бы распространилась от последнего слоя нейронной сети на предыдущий слой. И нам нужно повторить тот же алгоритм подстройки для нейронов, расположенных на предпоследнем слое. А затем - на предыдущем и так далее, пока мы не “упремся” в нейроны первого слоя, на котором действует та математика, которую мы рассматривали в предыдущем примере с однослойным перцептроном.
Есть одно замечание. Для упрощения, мы рассматривали только один нейрон на каждом слое. Но в реальности, слой нейронной сети может состоять из произвольного количества нейронов. Для обозначения номера нейрона на конкретном слое будем использовать нижние индексы. Так $a^{(L)}_i$ - это значение i-го нейрона на слое L нейронной сети. А $w^{(L)}_{jk}$ - это вес k-го входа j-го нейрона на том же слое. Количество нейронов на слое $L$ обозначим как $n_L$.
Следует иметь в виду, что на необходимое изменение значения нейрона на предыдущем слое будут оказывать влияние сразу несколько нейронов последующего слоя (а именно все нейроны последующего слоя). Поэтому для получения необходимого отклонения для данного нейрона нужно брать сумму всех производных, вычисленных для каждого нейрона последующего слоя:
В индексах здесь легко запутаться. Для более полного понимания алгоритма обучения нужно очень тщательно проследить все обозначения, лучше всего при помощи графического представления многослойного перцептрона. Для интуитивного понимания смысла его работы достаточно проследить все факторы, влияющие на значение нейрона на выходном слое, а также помнить, что если на величину влияет сразу несколько факторов, то алгоритм просто суммирует их влияние. Важно, что алгоритм обратного распространения ошибки для каждого нейрона абсолютно аналогичен. Именно поэтому не приходится как-то его модифицировать для разного количества нейронов и слоев. Поэтому он так удобен для обучения сложных и глубокий нейронных сетей.
Это лишь обзор алгоритма обучения и работы нейронных сетей. Это действительно очень сложная тема, поэтому не расстраивайтесь, если при первом знакомстве вы не смогли полностью понять математические методы и смысл действия этих алгоритмов и моделей. Детально рассмотрение видов, моделей нейронных сетей и алгоритмов их обучения - это отдельная и очень сложная область глубокого обучения, которая выходит далеко за рамки данного пособия. В этой главе мы лишь знакомимся с таким видом моделей машинного обучения, как нейронные сети на примере многослойного перцептрона. И на этом этапе достаточно интуитивного понимания принципов их работы.
Чем больше нейронов и слоев в нейронной сети, тем сложнее получаются модели. Количество нейронов в слое определяет, сколько признаков будет выделять данный слой из значений предыдущего для последующих. Количество же слоев выводит сложность модели на совершенно другой уровень. Это немного напоминает повышению степени полинома, хотя и не полностью аналогично. Важно понимать, что нейронные сети, особенно очень большие и глубокие - это очень сложные модели, которые могут быть склонны к переобучению. С другой стороны, именно глубокие нейронные сети способны решать очень сложные задачи анализа данных, особенно если данных в обучающей выборке очень много.
Но и небольшие и простые нейронные сети способны эффективно решать задачи простой классификации. Например, многослойный перцептрон с параметрами по умолчанию (1 скрытый слой с 100 нейронами) дает следующую границу принятия решений на модельных данных:
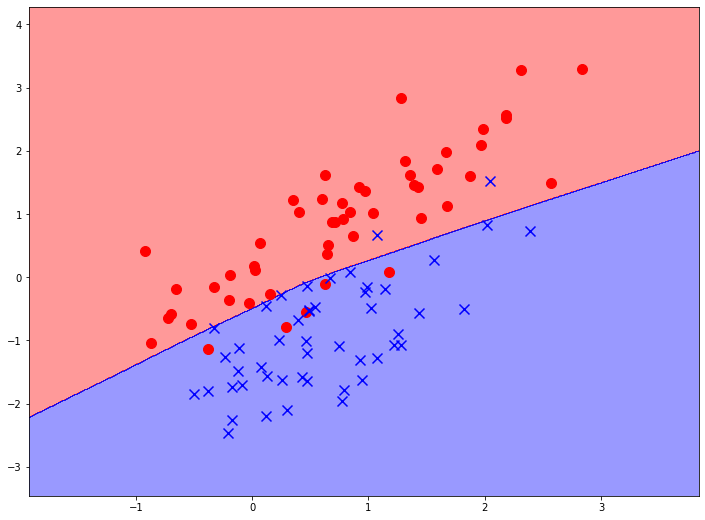
Та же конфигруация нейронной сети, но обученная на более сложном наборе данных так же неплохо справляется с их классификацией:
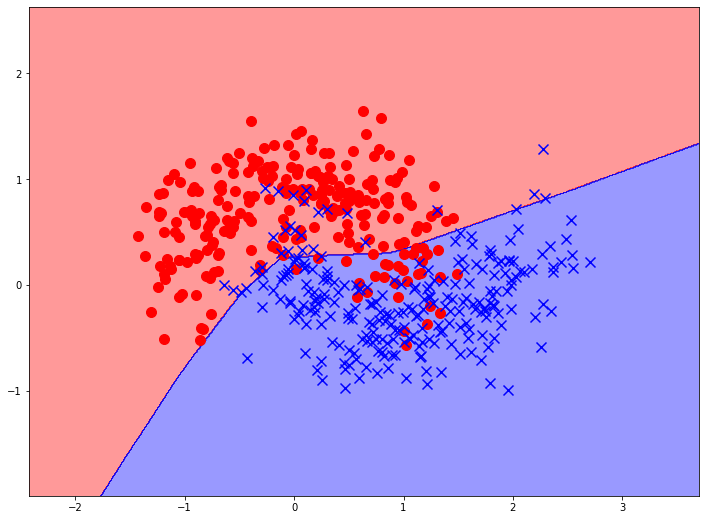
Если увеличить количество скрытых слоев, можно явно видеть усложнение формы границы принятия решения, что свидетельствует о повышении вариативности и сложности модели. При этом, в библиотечные реализации перцептрона встроены определенные механизмы предупреждения переобучения, что является главной бедой нейронных сетей на простых, малоразмерных задачах.
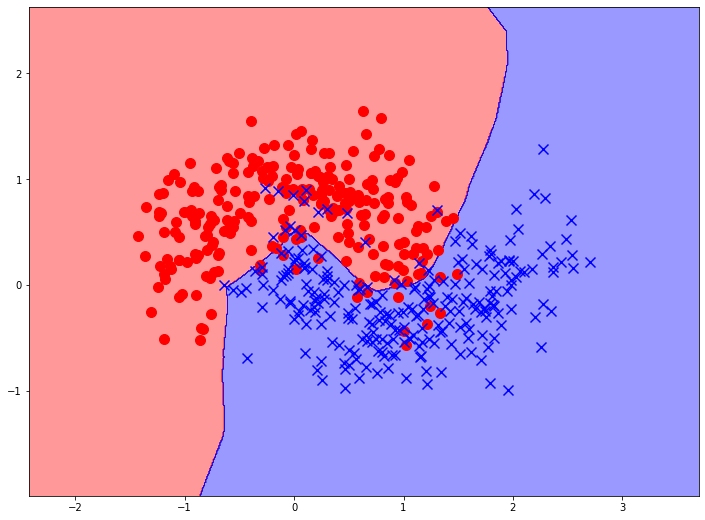
Одним из преимуществ нейронных сетей является их универсальность. Даже простые перцептроны могут разделять в задачах классификации данные, расположенные любым произвольным образом:
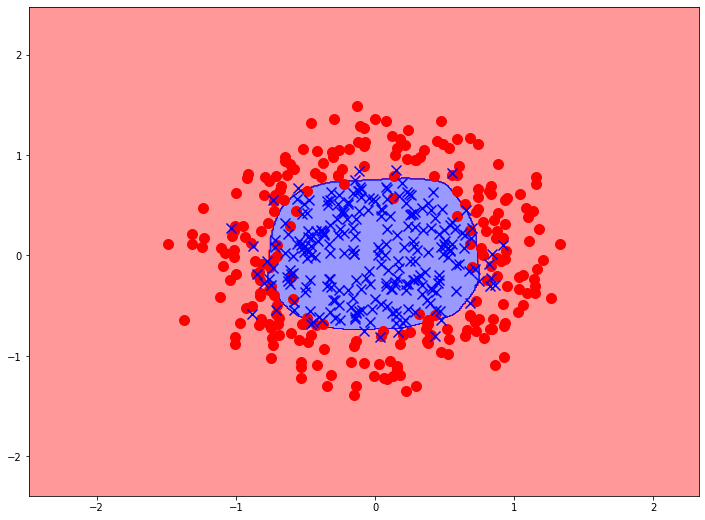
А что насчет задач регрессии? Нейронные сети очень легку приспособить для предсказания непрерывного значения. Для этого достаточно убрать функцию активации выходного нейрона. Можно сказать, что у последнего нейрона в качестве активации выступает тожественная функция ($y = x$). Тогда нейрон будет выдавать значение линейной комбинации, которая определена на всей числовой прямой. Алгоритм обучения, заметим, в таком случае вообще никак не изменяется! Обратим внимание, что, несмотря на линейность функции в последнем нейроне, вся модель, если она имеет хоть один скрытый слой является нелинейной из-за применения нелинейных функций активации на предыдущих слоях:
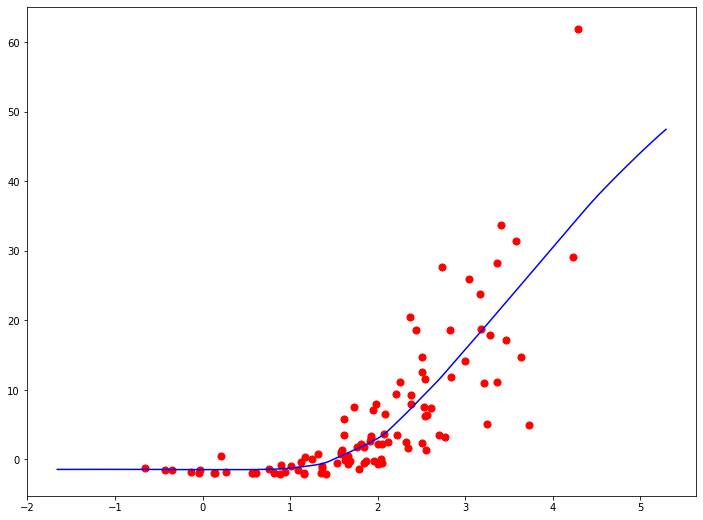
До сих пор мы говорили о моделях, на выходном слое которых только один нейрон. Они могут решать задачи бинарной классификации. Но что, если классификация множественная? В случае с нейронными сетями все очень просто. Мы создаем сеть, у которой на выходном слое несколько нейронов, по числу классов. Обучение такой модели предполагает, что при подачи на вход атрибутов объекта обучающей выборки, нейрон, соответствующий классу данного объекта должен показать 1, а остальные нейроны - 0. В остальном, алгоритм обучения такой сети остается без изменений. Тор есть мы просто кодируем в обучающей выборке значения целевой переменной единичными векторами, а нейронная сеть все сделает сама.
Точно так же просто можно использовать нейронные сети и для многоклассовой классификации. Для этого достаточно лишь отразить в обучающей выборке, что единица может присутствовать в нескольких выходных нейронах. Ну и, естественно, можно задать данные для нечеткой классификации. В этом смысле в полной мере раскрывается универсальность нейронных сетей.
Количество слоев и количество нейронов на каждом слое, а также порядок их соединения называется архитектурой нейронной сети. Вопрос выбора архитектуры нейронной сети зачастую решается произвольно, “на глаз”, исходя из соображений диагностики переобучения, про которую мы будем говорить в следующей части учебника. Определенные типы архитектур нейронных сетей традиционно применяются для анализа разных видов информации. Например, сверточные нейронные сети хорошо показывают себя в обработке изображений, рекуррентные сети - в анализе временных рядов, звуков речи, генеративные сети - в создании изображений и текстов, трансформеры - в анализе естественных текстов. Говоря о перцептронах, есть несколько эмпирических правил, которые могут помочь в выборе архитектуры сети. Количество нейронов на входном и выходном слое фиксировано и определяется данными в обучающей выборке. Количество скрытых слоев зависит от сложности задачи. И обычно нет смысла увеличивать количество нейронов в слоях. То есть если на каком-то слое, допустим, 16 нейронов, то на следующем можно сделать 16, 8, 4 и так далее, но нет смысла делать 50. Существуют автоматизированные способы подбора архитектур нейронных сетей, но они требуют невероятно больших вычислительных мощностей.
Основное преимущество нейронных сетей перед остальными моделями машинного обучения состоит в том, что они очень легко масштабируются. Возьмем простой двухслойный перцептрон, который мы рассматривали чуть выше. Если представить его в виде одной формулы, это будет очень сложная формула - ведь это логистическая функция, считающаяся от линейной комбинации трех других логистических функций от линейной комбинации трех входных переменных. Возьметесь дифференцировать эту функцию для метода градиентного спуска? А в виде нейронной сети эта модель представляется довольно простой, последовательной, даже в чем-то понятной. В этом очень помогает универсальный алгоритм обратного распространения ошибки, который позволяет произвольно задавать количество нейронов и слоев, без экспоненциального усложнения математического аппарата, необходимого для обучения такой модели.
Именно поэтому, нейронные сети позволяют строить очень сложные и вариативные модели для решения таких задач, на которых более традиционные модели недообучаются. Самые современные нейронные сети для, например, анализа и генерации текстов на естественных языках могут иметь десятки триллионов обучаемых параметров. Модели такого уровня сложность просто невозможно построить при помощи других алгоритмов, которые относятся к классическому машинному обучению.
Конечно, обучение таких гигантских моделей требует огромных вычислительных мощностей. Такие модели обучаются месяцами на самых современных суперкомпьютерах и кластерах. Вообще, глубокие нейронные сети, даже более скромные по размерам - это довольно вычислительно емкие модели. Но при этом, рост вычислительной сложности гораздо меньше, чем для других видов моделей. Ведь алгоритм применения (прямого распространения) и обучения (обратного распространения) нейронных сетей очень хороше векторизуются, то есть представляются в матричной форме. А компьютеры могут очень эффективно выполнять матричные операции, потому что они легко распраллеливаются. Именно поэтому обучение и применение нейронных сетей сильно выигрывает от применения вычислений на графических картах.
Но есть у нейронных сетей и недостатки. Кроме уже упомянутой вычислительной емкости, одним их главных является их неинтерпретируемость. Нейронные сети работают по принципу черного ящика - сигналы на входе, сигналы на выходе. Что происходит внутри, что значит каждый конкретный параметр - никто не знает. Это может показаться несущественным, но в некоторых областях применения, важно не только эффективное предсказание, но и объяснение выданного значения. Это очень сильно ограничивает применение нейронных сетей в таких областях как здравоохранение, государственной управление, социальная сфера и других подобных. Причем, чем больше и сложнее нейронная сеть, тем большей загадкой является ее внутренняя структура и принцип работы.
Выводы:
- Нейронные сети являются самым популярным методом обучения с учителем.
- Нейронные сети позволяют строить самые сложные и масштабируемые модели.
- Обучение и применение нейронных сетей очень хорошо распараллеливается. За счет этого можно ускорять их работу с помощью графических ядер и других средств.
- Перцептрон - самая простая архитектура нейронной сети, состоящая из нескольких полносвязных слоев.
- Нейронные сети работают по принципу черного ящика, их очень сложно интерпретировать.
- При применении нейронных сетей встает вопрос выбора архитектуры, количества нейронов.
- Главный параметр нейронной сети - количество скрытых слоев. Если их больше одного сеть называется глубокой.
- Нейронные сети очень естественно решают задачу множественной и мультиклассовой классификации.
Деревья решений
Деревья решений - это один из самых простых, но при этом популярных методов обучения с учителем. Они применяются как для построения моделей классификации или регрессии, так и для анализа данных, чтобы получить полезную информацию о некоторых зависимостях в них. Основное преимущество деревьев решений - понятность алгоритма и простота интерпретации результатов.
Дерево решений - это иерархическая структура, состоящая из правил вида “Если …, то…”. Примерно так же будет рассуждать человек, которому поставлена задача определить по имеющимся характеристикам объекта значение целевой переменной. В узлах дерева содержатся некоторые условия, или критерии, по отношению к которым объект может быть отнесен к одному из вариантов. Как правило, данные критерии бинарные и выражаются в оценке значения одного из признаков. Чаще всего при использовании непрерывных шкал признаков используется сравнение с пороговым значением.
По результатам проверки в узле мы может пойти по одному из ребер и попасть либо в следующий узел с другой проверкой, либо в листьевой элемент, в котором содержатся значение целевой переменной. Если это задача классификации, то это конкретная метка класса. Если это задача регрессии - то это чаще всего конкретное значение целевой переменной. Однако, может использоваться линейная функция от признаков (В каждом листе - разная). Таким образом решается задача моделирования целевой переменной.
В машинном обучении деревья стоит задача нахождения оптимального дерева решений - такого дерева, который наилучшим образом предсказывает значение целевой переменной. Обучение - это подбор параметров. Параметрами дерева являются конкретные значения порогов в каждом узле. Также скрытым параметром является порядок “опроса” признаков.
Для построения дерева решений в первую очередь необходимо решить, по какому признаку мы будем разделять выборку. Для этого используются определенные критерии. Чтобы понять, что такое критерий, давайте рассмотри следующую выборку данных для бинарной классификации:
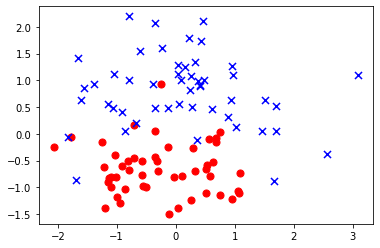
По какому признаку лучше разбить выборку на две части - на отложенному по горизонтально оси (первому) или по вертикальной (второму)? Заметим, что разбиение выборки можно изобразить на графе как пряму линию, перпендикулярную той оси, по которой мы разбиваем. Очевидно, что разбиение по второму признаку (проведение горизонтальной линии) гораздо более целесообразно, ведь в итоге мы получим значительно более однородные подвыборки - в одной будет больше красных объектов, а в другой - синих. Если же мы проведем вертикальную линию, где бы мы ее не провели, две подвыборки будут примерно в равных пропорциях содержать как объекты обоих классов.
Это, конечно, искусственный пример, в котором ответ очевиден. В реальности нам нужен математический механизм, который измеряет, насколько “неоднородными”” станут выборки после разделения по одному из признаков. Для этого чаще всего используются информационная энтропия, вариация или критерий Джини. Рассмотрим наиболее распространенную меру неоднородности выборки для категориальных значений, информационную энтропию:
В данной формуле $s$ - это некоторая выборка, среди элементов которой встречаются $c$ разных значений. $p_i$ - это вероятность (частота) появления значения $i$. Информационная энтропия выборки показывает, насколько неоднородно их распределение. Если разных значений в данной выборке примерно поровну, значение информационной энтропии будет близко к 1, чем чаще будет встречаться одно значение, тем ближе будет значение к 0. Для признаков, измеряемых по числовым, непрерывным шакалам, вместо энтропии используется простая вариация выборки.
Для выбора условия разбиения выборки подсчитывают специальную метрику, называемую прирост информации. Она вычисляется по следующей формуле:
где $d$ - вся выборка, до разделения, $s$ - подвыборка. То есть мы считаем сумму энтропии подвыборок после разделения и сравниваем ее с энтропией исходной выборки. Весь алгоритм нахождения оптимального разбиения сводится к тому, чтобы найти такое разбиение, у которого прирост информации наибольший.
Такой алгоритм способен решать как задачи классификации, так и задачи регрессии. Так как прирост информации вычисляется по распределению именно целевой переменной, в классификационных задачах используется мера энтропии, а в регрессионных - вариация, вот и все различие.
Построение дерева решений - это итеративный процесс, в котором на каждой итерации находится оптимальный признак и его пороговое значение, которое лучше всего разбивает выборку на две подвыборки. Затем процесс повторяется для каждой из двух подвыборок, пока не будет достигнуто некоторое условие остановки алгоритма. Процесс разбиения выборки может окончится двумя способами. Естественный - это когда в выборке остаются объекты только одного из классов. Искусственный - это достижение критерия остановки. В качестве критерия чаще всего используется максимальная глубина дерева. Но можно задать, например, минимально количество объектов в узле.
Давайте рассмотрим процесс построения дерева решений на примере простой задачи бинарной классификации. Для использования библиотечной реализации дерева решений нужно всего лишь создать объект соответствующего класса и указать максимальную глубину дерева. Для начала построим дерево глубиной 1 узел:
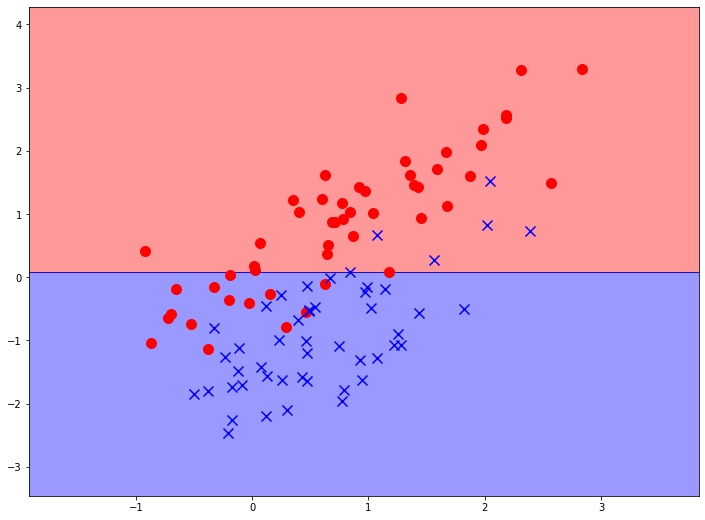
Мы видим, что модель сделала только одно разделение. Модель выбрала признак, отложенный на вертикальной оси, а также значение этого признака (чуть больше 0), которое максимизирует прирост информации после разделения исходной выборки. Теперь у нас есть две подвыборки (назовем их верхней и нижней), причем ясно видно, что в нижней части заметно больше синих объектов, а в верхней - красных.
Если мы сейчас остановимся, модель будет классифицировать все объекты из верхней выборки как красные (так как красных там большинство), а все объекты из нижней - как синие. Это лучше, чем случайное угадывание, но все равно присутствует довольно большая ошибка классификации. Чтобы ее уменьшить, можно увеличить глубину дерева - тогда модель продолжит делить выборку, чтобы получить все более точную классификацию.
Теперь построим дерево глубиной два уровня. Так как алгоритм обучения деревьев решений является жадным, то первое разделение будет таким же, но добавится еще одно. Поэтому, строя деревья решений разной глубины на одних и тех же данных, мы можем наблюдать, как “растет” в глубину одно и то же дерево. На графике мы видим границу принятия решения, показывающую еще одно деление - теперь по другому признаку (вертикальный отрезок):
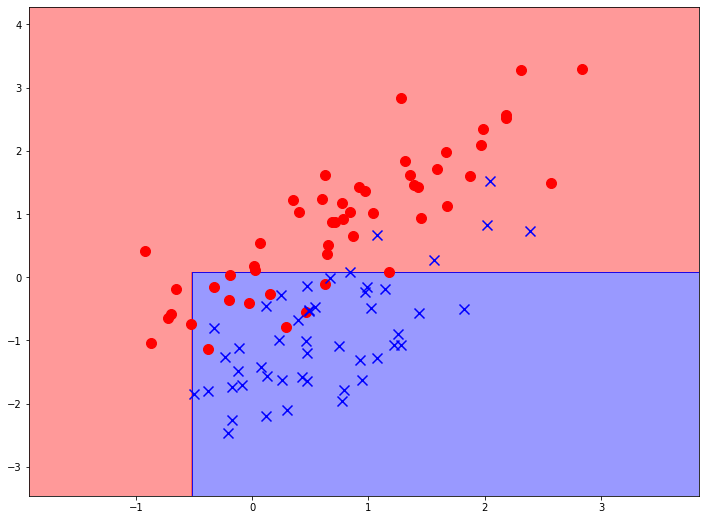
Обратим внимание, что это деление затрагивает только нижнюю подвыборку. Верхняя никак не делится и так же, как и в предыдущей модели будет отнесена к красному классу. В нижней же подвыборке модель опять произвела поиск наилучшего деления (но в формуле уже сравнивалась энтропия только нижней подвыборки до и после деления). Модель выбрала горизонтальный признак и значение примерно 0,5. Давайте продолжим увеличивать глубину дерева:
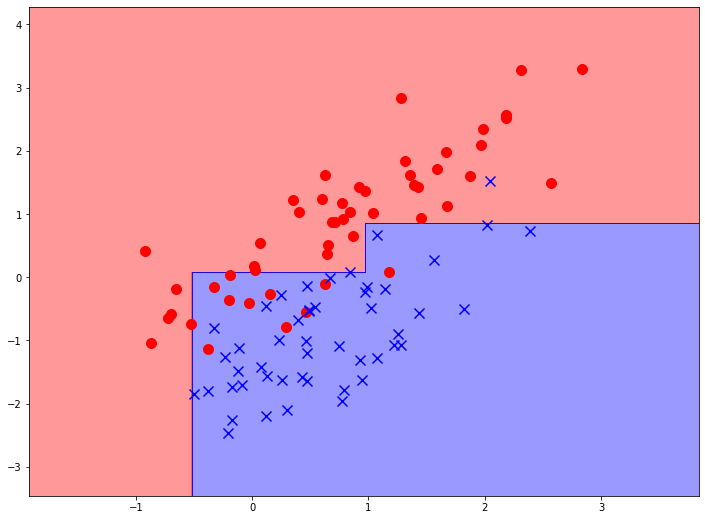
При глубине 3 мы уже видим несколько дополнительных делений. Рассматривая каждое из них можно убедиться, что оно еще немного увеличивает неоднородность разделения всех точек выборки. Увеличивая глубину дерева еще можно заметить уже не очень однозначное поведение модели:
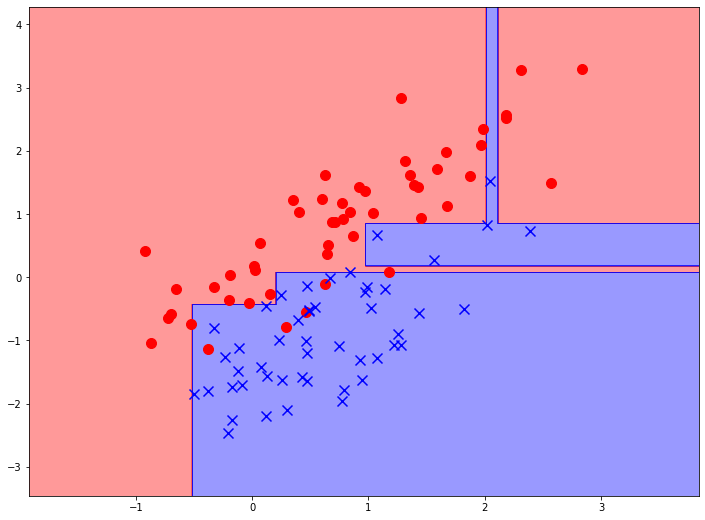
Мы видим еще некоторые деления. И они явно имеют “цель” отнести к правильному классу определенные объекты выборки. Является ли такое решение модели целесообразным? Модель следует своей математической формулировке. Но глядя на график, можно сделать вывод, что некоторые узлы дерева не очень “показательны”, то есть отражают положение конкретных точек данных, на не общие тенденции в целом. Это явление станет еще более явным, если мы увеличим глубину дерева до 10:
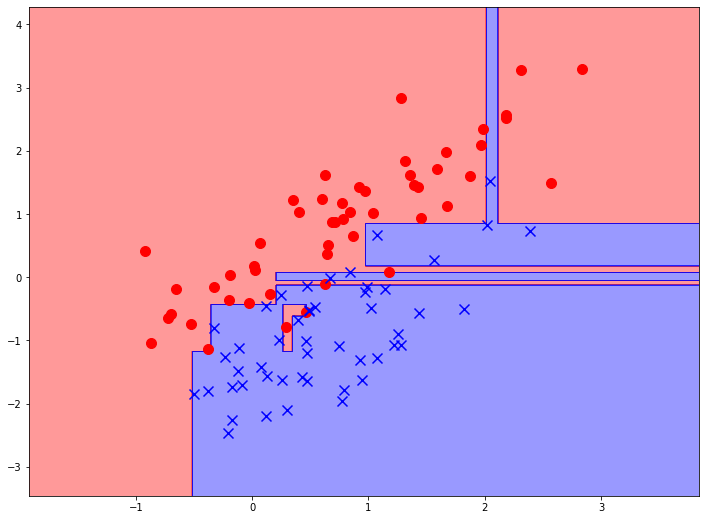
Здесь явно модель начинает “увлекаться” вылавливанием отдельных точек. Это явление называется переобучением, и более подробно мы будем говорить о нем дальше. Дело в том, что с ростом глубины дерева модель становиться более сложной и чувствительной, что не всегда может быть хорошо. Плюс к этому у нас не так много данных (точек выборки), чтобы строить такие глубокие деревья. Именно поэтому, максимальную глубину дерева стоит ограничивать. Причем сколько именно уровней использовать зависит только от структуры данных.
Можно заметить, кстати, что модель, изображенная на последнем графике достигает 100%-ной эффективности, то есть разделяет выборку полностью правильно. Причем, если посчитать количество делений, там явно не наберется на 10 уровней. Это происходит потому, что как только по одной из веток дерева получается выборка из одного класса, рост дерева по этой ветке прекращается. То есть дерево решений достигло своего естественного предела.
Можно воспользоваться специальной библиотечной функцией для визуализации самого дерева решений в виде графа:
1
2
3
from sklearn.tree import plot_tree
plt.figure(figsize=(12, 9))
plot_tree(clf)
Данный код, вызванный для дерева с максимальной глубиной 3 даст такую картину:
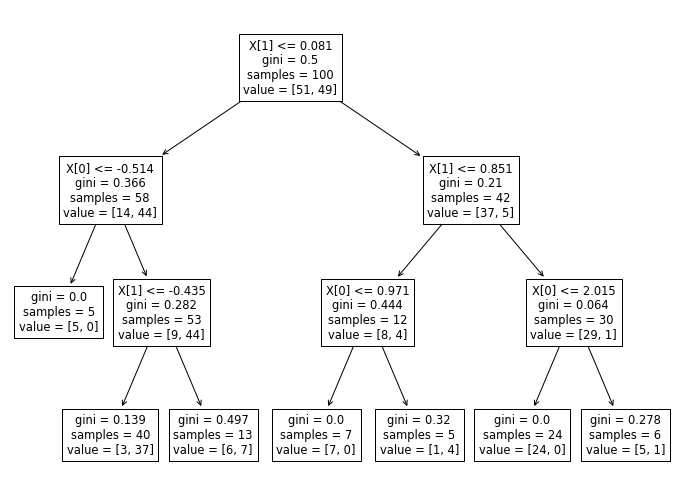
На этом графе мы видим уже знакомые нам деления: корневой узел с пороговым значением 0,081 (близкое к 0 значение) по второму признаку - это наша горизонтальная линия на первом графике. И каждый другой узел соответствует отрезку на графике. Можно заметить также узел (крайний слева), который “досрочно” выделяет подвыборку, состоящую из одного класса. Рост дерева, как мы видим, в этом месте прекратился.
Дерево решений, как мы говорили, подходит и для задач регрессии. Хотя, его не так часто применяют в регрессионных задачах. Но в определенных случаях эта модель может дать интересный результат. Давайте рассмотрим применение модели дерева решений для задачи парной регрессии:
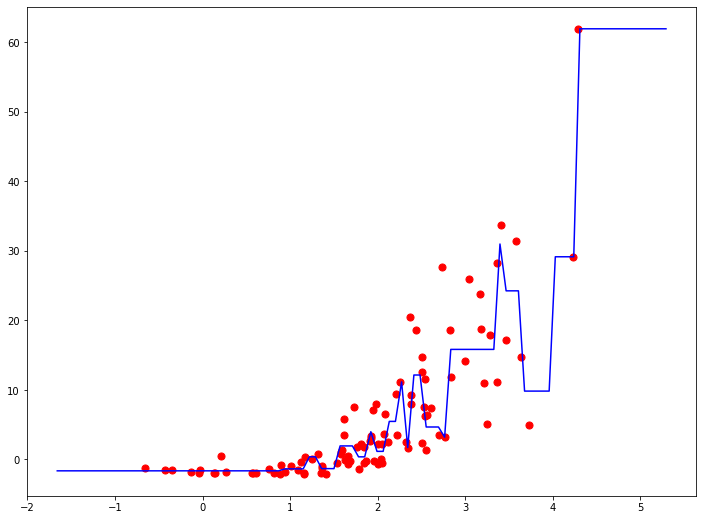
Как мы видим, Линия регрессии состоит из горизонтальных участков. Это логично, ведь в листьевых элементах дерева будут стоять конкретные значения целевой переменной. Отсюда следует область применения таких моделей. Деревья решений для регрессии хорошо работают, если в данных наблюдается кусочно-линейная, ступенчатая зависимость. Более плавные, нелинейные зависимости деревья улавливают плохо. На данном графике мы это ясно видим - модель явно переобучена и ведет себя слишком хаотично. Можно также посмотреть визуализацию данной модели в виде дерева:
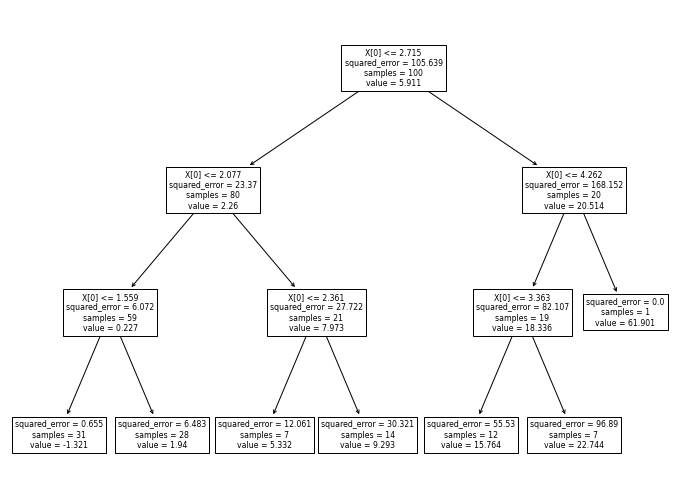
Попробуйте самостоятельно соотнести узлы данного дерева с участками линии регрессии.
Деревья решений имеют ряд заметных преимуществ перед другими моделями машинного обучения. Главное среди них - это прекрасная интерпретируемость получаемых моделей. Обучив модель на выборке мы можем не просто получить предсказание, но и проследить ход “рассуждений” модели, понять, почему модель приняла именно такое решение, какие факторы на него повлияли. Кроме того, при анализе модели можно решить вопрос, что следует изменить, чтобы модель выдавала другой результат. Все это делает деревья решений важным инструментом не только моделирования, но и предварительного анализа данных.
Например, деревья решений могут быть использованы для анализа так называемой важности признаков. Чем чаще конкретный признак используется в дереве для разбиения выборки, тем более влияние его значения оказывают на целевую переменную. Можно построить график относительной важности признаков и исходя из него принимать определенные решения о преобразовании данных, например, неважные признаки можно убрать из датасета. И даже если для моделирования будет применяться какой-то другой вид модели, дерево решений часто пригождается на этом предварительном этапе.
Кроме того надо сказать, что деревья решений - достаточно экономный вид модели в плане требовательности к вычислительным ресурсам. Они строятся довольно быстро даже на больших выборках. Вдобавок, эта модель очень нетребовательна к характеру данных. Например, она одна из немногих не требует преобразования категориальных признаков в числовые. Об этом более подробно мы будем говорить в следующих главах. Дереву решений не мешают лишние, непоказательные признаки в датасете. Модель просто не будет их использовать для разбиения. Деревья решений нечувствительны к нормированию данных и к выбросам. В целом это очень непритязательная модель, но несмотря на это она бывает эффективна гораздо чаще, чем можно предположить.
Выводы:
- Дерево решений - это граф, в узлах которого содержатся некоторые условия (как правило, пороговые условия по признаку)
- Деревья решений являются одним из самых популярных методов классического машинного обучения.
- Используются как для построения модели, так и для предварительного анализа данных.
- Дерево решений просто построить, ему не требуются огромные вычислительные мощности.
- Деревья решений - интерпретируемый метод, его можно объяснить и понять, особенно при малых глубинах дерева.
- Деревья решений более лояльны к входным данным - могут работать с категориальными признаками.
- Деревья решений склонны к переобучению при достаточно больших глубинах.
- Дерево решений очень толерантно к лишним признакам в наборе данных.
- Существуют специальные виды распределений, которые сложно описываются деревьями решений.
K ближайших соседей
Еще один метод обучения с учителем - метод ближайших соседей - настолько прост, что иногда его вообще не относят к машинному обучению. Тем не менее, на практике он используется довольно часто, в основном для задач классификации, и в некоторых задачах может быть очень эффективным. В его основе лежит простой принцип - предсказывать для данного объекта такое значение целевой переменной, которое имеют ближайшие к нему объекты обучающей выборки.
Для использования этого метода надо определить понятие расстояния. Так как чаще всего данные в машинном обучении представляют собой численные вектора, удобнее всего использовать расстояние Евклида. То есть под расстоянием понимается квадратный корень из суммы квадратов разностей значений каждого атрибута (измерения) у каждой из двух векторов (точек данных). Выбор именно такой функции расстояния ничем не обоснован, но на практике работает достаточно неплохо. Если мы анализируем какие-то специфические типы данных, то можно использовать и другие функции расстояний. Например, для категориальных признаков часто используется расстояние Хэмминга.
Другими словами для классификации объекта модель ищет некоторое количество объектов обучающей выборки и смотрит, какие значения целевой переменной имеют эти объекты. Самый простой вариант - найти ближайший к данному объект из обучающей выборки и приписать данному объекту такое же значение целевой переменной. Это обосновано так называемой гипотезой компактности - предполагается, что близкие по характеристикам объекты (то есть имеющие схожие значения атрибутов) будут иметь схожие значения целевой переменной. В некоторых задачах гипотеза компактности может не выполняться - тогда и метод ближайших соседей будет работать не так эффективно. Посмотрим, как этот принцип работает в задаче классификации:
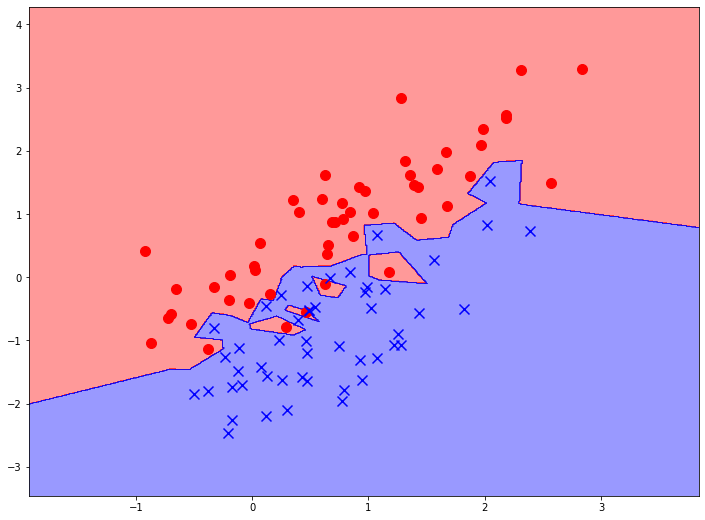
На графике мы видим, что каждая точка графика отнесена к тому классу, который имеет ближайшая к нему точка обучающей выборки. На этом графике отчетливо видно, что при наличии случайных отклонений в данных, класс ближайшего соседа может быть не совсем показателен. Мы видим “анклавы” одного класса внутри области другого. Понятно, что они образовались из-за того, что какая-то точка одного класса попала в область, заполненную точками другого класса. Но действительно ли это имеет значение для прикладной задачи? Может, имеет смысл брать не одного ближайшего соседа, а несколько. В задачах бинарной классификации чаще всего берут нечетное количество соседей, чтобы избежать “ничейных ситуаций”. Вот как выглядит классификация тех же данных, но при учете пяти ближайших соседей:
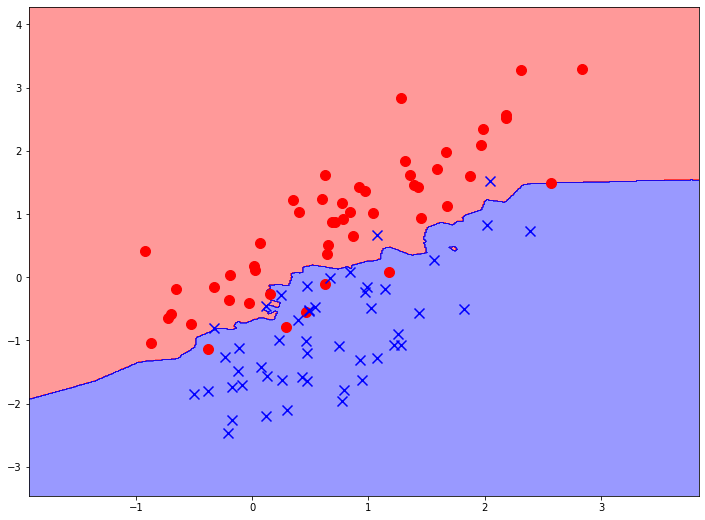
Мы видим, что граница принятия решения значительно сгладилась. Многие анклавы исчезли. Более того, на этом графике некоторые точки располагаются на фоне другого цвета. Это значит, что модель бы отнесла их к другому классу. То есть, модель сделала бы ошибку в обучающей выборке. Такая ситуация принципиально невозможна в случае с одним соседом. Другими словами при $k=1$ модель всегда имеет абсолютную, 100%-ю эффективность на обучающей выборке. Но это не значит, что такая модель лучше всего работает на практике. Иногда данные содержат выбросы, аномалии и непоказательные объекты, а значит, увеличение количества рассматриваемых соседей в этом методе ($k$) может положительно сказаться на применимости модели.
Давайте еще увеличим $k$ до 20 и посмотрим, как изменяется граница принятия решений:
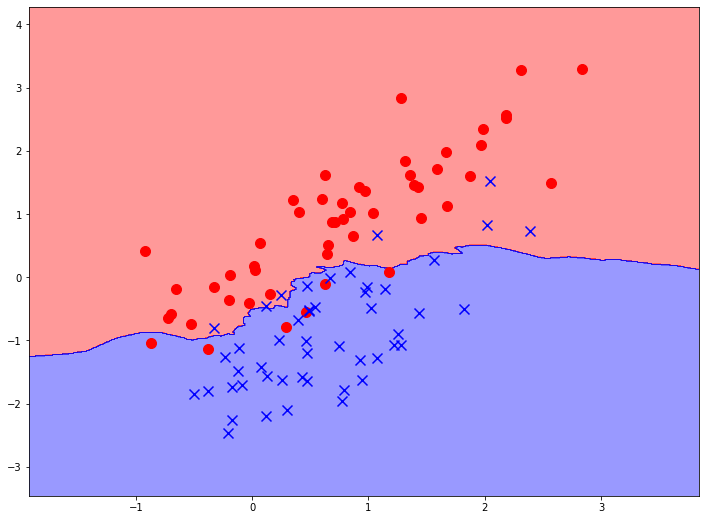
Мы видим, что она еще больше сгладилась и выровнялась. И в целом, чем больше $k$, тем проще получается граница принятия решения. Этим данный алгоритм отличается от всех других классов моделей машинного обучения. Обычно чем сложнее модели и чем больше у нее параметров, тем вариативнее и сложнее получается граница принятия решения. С методом ближайших соседей все наоборот: чем больше объектов мы принимаем в расчет, тем проще и менее вариативными получаются предсказания. В самом предельном случае, если $k$ будет равно количеству объектов в обучающей выборке, модель всегда будет предсказывать самый популярный класс.
Так как же подобрать оптимальное значение $k$? Надо понимать, что с увеличением количества анализируемых соседей повышает надежность и достоверность предсказания. Уменьшение этого параметра может дать учет более тонких и слабых зависимостей в данных, но повышает влияние шумов в данных на результаты. Как мы увидим позже, модели с маленьким $k$ склонны к переобучению, а с большим - к недообучению.
Если позволяют ресурсы, можно построить несколько моделей с разным количеством соседей и сравнить их эффективность. Например, с этим может помочь метод кросс-валидации, который мы будем рассматривать позже. Для первоначального значения $k$ зачастую пользуются следующим эмпирическим правилом: количество соседей выбирают примерно равным квадратному корню из количества объектов выборки. Так, если в выборке 100 точек, можно начать с модели, учитывающей 10 соседей. Для выборки в 1000 точек можно попробовать 31 соседа. Это не жесткое правило, и оно не подкрепляется какими-то доказательствами эффективности, это просто практическая рекомендация.
В задачах множественной классификации уже нельзя задать количество соседей так, чтобы исключить ничейные ситуации. Такие коллизии можно решать по-разному, но чаще всего принимают во внимание ранг соседа, то есть более близкие соседи будут иметь преимущество перед более далекими. Это еще одно использование гипотезы компактности.
А как этот метод решает задачи регрессии? Да примерно так же, только в качестве предсказываемого значения целевой переменной обычно берется среднее значение целевой переменной ближайших соседей. Вот пример работы метода (здесь $k=5$) на задаче парной регрессии:
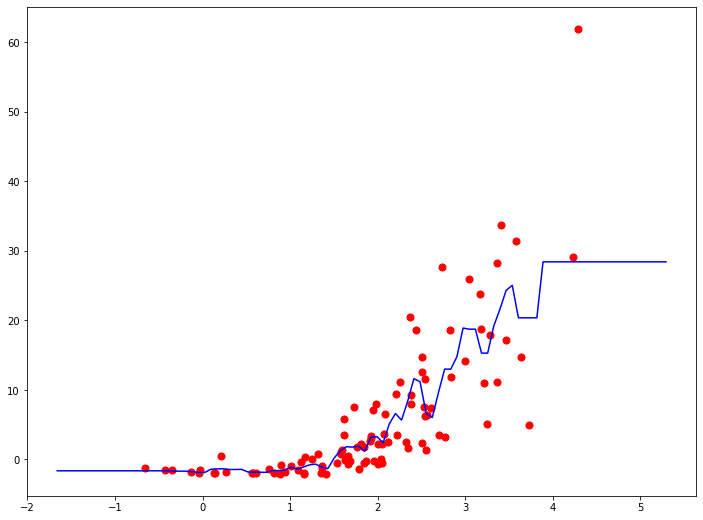
На графике можно увидеть горизонтальные участки - это те точки, для которых пять ближайших соседей не меняются. Поэтому и не меняются и их средние. В данной модели вычисляется простое среднее арифметическое всех нужных соседей. Этот алгоритм называется простое невзвешенное голосование. То есть каждый объект их числа ближайших соседей имеет как бы одинаковый голос. Но существуют варианты алгоритма ближайших соседей для регрессии, в которых считается средневзвешенное значений у соседей. Таким образом, на предсказываемое значение целевой переменной для данной точки будут больше влиять точки выборки, которые находятся ближе к ней. Такая схема называется взвешенное голосование. Эти две схемы могут применяться как в регрессионных, так и в классификационных задачах.
Давайте попробуем реализовать метод ближайших соседей самостоятельно, без использования библиотечных функций. Он настолько прост, что на это потребуется всего несколько строчек кода. Для этого ограничимся только задачей классификации, то есть будем предсказывать наиболее популярный класс среди соседей. Для этого создадим класс, и определи м в нем инициализатор, в котором запоминаем необходимое количество соседей и функцию расстояния:
1
2
3
4
5
class KNN:
def __init__(self, k=3):
self.k = k
def distance(self, a, b):
return np.sqrt(np.sum((a - b)**2))
Теперь реализуем функцию предсказания. Для этого сначала напишем вспомогательную функцию, осуществляющую предсказание только по одному объекту:
1
2
def _predict(self, x):
distances = [self.distance(x, x_train) for x_train in self.X_train]
Здесь мы вычислили расстояние переданного объекта до каждого объекта обучающей выборки. Теперь нам нужно будет отсортировать этот массив, чтобы найти ближайшие объекты к данному. Но при сортировке потеряется порядок, то есть номер соответствующего объекта выборки. А нам это важно, так как по номеру (индексу) мы потом сможем получить значение его целевой переменной (класса). Поэтому нужно записать в массив и номера элементов. Это можно сделать, например, так:
1
distances = list(enumerate(distances))
Теперь мы можем отсортировать этот массив. Для этого воспользуемся сортировкой со вспомогательной функцией, так как мы будем сортировать именно по расстоянию, которое стало у нас вторым элементом кортежа:
1
distances.sort(key=lambda elem: elem[1])
Далее оставляем только список индексов, то есть номера ближайших соседей, и сразу из этого списка получаем значения их целевых переменных:
1
2
indicies = [idx for idx, _ in distances]
neighbors = [self.y_train[i] for i in indicies[:self.k]]
Теперь нам осталось лишь подсчитать моду в этом массиве, то есть самое популярное значение. Сделать это, опять же, можно по-разному, мы воспользуемся коллекцией Counter из стандартной библиотеки python:
1
from collections import Counter
1
2
most_common = Counter(neighbors).most_common(1)
return most_common[0][0]
Напомним, это метод предсказания класса только одного объекта. Чтобы можно было предсказывать класс по списку обернем этот метод:
1
2
3
def predict(self, X):
y_pred = [self._predict(x) for x in X]
return np.array(y_pred)
А в чем заключается обучения метода ближайших соседей? И где его внутренние параметры? Вот почему его иногда вовсе не относят к методам машинного обучения: этот метод не требует подбора параметров, у него их просто нет. Обучение заключается в том, что модель должна запомнить всю обучающую выборку:
1
2
3
def fit(self, X, y):
self.X_train = X
self.y_train = y
Эти поля класса мы уже использовали выше для предсказания. Можно считать, что параметрами метода ближайших соседей является сама обучающая выборка.
Вот так выглядит итоговый класс, который реализует метод ближайших соседей для классификации:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class KNN:
def __init__(self, k=3):
self.k = k
self.X_train = None
self.y_train = None
def distance(self, a, b):
return np.sqrt(np.sum((a - b)**2))
def fit(self, X, y):
self.X_train = X
self.y_train = y
def predict(self, X):
y_pred = [self._predict(x) for x in X]
return np.array(y_pred)
def _predict(self, x):
distances = [self.distance(x, x_train) for x_train in self.X_train]
distances = list(enumerate(distances))
distances.sort(key=lambda elem: elem[1])
indicies = [idx for idx, _ in distances]
neighbors = [self.y_train[i] for i in indicies[:self.k]]
most_common = Counter(neighbors).most_common(1)
return most_common[0][0]
В процессе реализации данного алгоритма можно отчетливо понять его достоинства и недостатки. К несомненным достоинствам данного метода относится его простота и очень быстрое обучение. Так как самого обучения фактически нет, это выгодно отличает данный метод от более сложных и глубоких методов обучения, которые могут тратить на оптимизацию своих параметров огромное количество вычислительных ресурсов.
Скорость обучения компенсируется процессом предсказания. Самым главным недостатком этого метода является то, что для предсказания нужно хранить в памяти всю обучающую выборку. При больших объемах это может быть очень медленно или вообще непрактично. Все остальные модели для предсказания используют только оптимальные значения параметров. Обучающая выборка нужна только для их подбора. Поэтому именно этот алгоритм, в отличие от всех остальных очень быстро учится и довольно медленно работает. Вообще, вычислительная сложность предсказания растет пропорционально квадрату размера обучающей выборки. Поэтому очевидно, что это может стать проблемой при большом количестве обучающих примеров.
И это ограничивает его применимость данного метода. Например, метод ближайших соседей практически никогда не используют в задачах, чувствительных ко времени отклика, таких как обработка изображений или видео в реальном времени. Его неудобно или вообще невозможно использовать на устройствах с ограниченным объемом памяти.
Кроме этого следует отметить интерпретируемость данного метода. Предсказания по алгоритму ближайших соседей очень легко объяснить и понять. В некоторых сферах это может быть очень полезно. Кроме того, алгоритм не очень чувствителен к выбросам и аномальным значениям. Это позволяет меньше уделять внимания очистке данных и поиску непоказательных объектов. При этом чем больше соседей анализируется, тем меньше влияние таких аномалий и выбросов - они просто усредняются.
Зато этот алгоритм не очень эффективен в задачах и дисбалансом классов. Так как решение основано на подсчете количества объектов определенного класса, если объектов одного класса значительно больше в выборке, он будет доминировать и в голосовании. Поэтому перед применением этого метода обязательно провести анализ и при необходимости исправление дисбаланса классов.
Данные для метода ближайших соседей всегда обязательно нормализовать. Это связано с тем, что если размерность данных неодинакова по разным измерениям (признакам), то более крупномасштабный признак будет доминировать при вычислении функции расстояния. Например, если все признаки измеряются в долях единицы, а один - в миллионах, то расстояния по этой оси будут всегда значительно больше, чем по другим. Расстояния по другим измерениям вообще не будут заметны в общей сумме. Поэтому важно, чтобы данные имели одинаковый масштаб по всем признакам. О нормализации данных мы уже говорили в предыдущих главах.
Обычно в методе ближайших соседей подразумевается, что все признаки дают одинаковый вклад в общую меру расстояния. Но при анализе предметной области мы можем сделать вывод, что разные признаки в разной степени влияют на целевую переменную. В таком случае признакам может быть придан вес, который регулирует степени влияния расстояния именно по данному измерению в общее расстояние между точками. Такой учет значимости признаков может повысить качество модели. Но для этого обычно не модифицируют функцию расстояния, а изменяют нормализацию признаков. Обычные признак, которые имеют влияние (вес) 1 будут нормализованы к шкале [0; 1]. Если признак имеет меньшее влияние, то ему может быть придан вес, например, 0.3 и тогда он будет приведен к шкале [0; 0.3] (то есть признак просто умножается на свой вес). За счет этого, он будет давать меньший вклад в общее расстояние и таким образом учитываться меньше. Более же важный признак может иметь вес больше единицы, и шкалу измерения, например, [0; 20]. Так, его влияние будет значительно больше. Это прием называется растяжение осей.
Метод k ближайших соседей - самый простой, но не бесполезный алгоритм обучения с учителем. Он имеет свои особенности и очень отличается от других моделей машинного обучения. Он не применяется для анализа больших данных, высокопроизводительных вычислений и нечасто применяется для регрессий. Но для простых задач классификации он зачастую бывает очень полезен.
Выводы:
- Метод ближайших соседей заключается в предсказании значения исходя из значения ближайших к нему объектов обучающей выборки.
- Опирается на гипотезу компактности: схожие объекты чаще принадлежат одному классу, чем разным.
- Чаще всего используется евклидова метрика расстояния между объектами.
- Не имеет внутренних параметров. Можно считать, что параметры - это сама обучающая выборка.
- Нужно выбрать k - количество используемых соседей.
- Чем больше k, тем проще модель и больше вероятность недообучения.
- Самый простой алгоритм для классификации.
- Данные обязательно надо нормализовать.
- Алгоритм не чувствителен к выбросам.
- Алгоритм работает медленно при большом объеме обучающей выборки.
Наивная байесовская модель
Еще одним классом моделей обучения с учителем является так называемый наивный байесовски классификатор или наивная байесовская модель. Как следует из названия, этот алгоритм используется только для классификации. В отличие от других методов он в принципе не подходит для решения регрессионных задач. Если вы изучали математическую статистику или теорию вероятности, вы можете предположить, что эта модель использует формулу или правило Байеса.
Эта модель оценивает вероятность определенного значения целевой переменной при данных значениях признаков. Чтобы понять принцип ее работы нужно познакомится с основными понятиями теории вероятностей. Если вы уже изучали ее, о смело переходите на описание самого алгоритма работы наивного классификатора. Если же вы не знакомы с основными уравнениями или вам требуется повторение, приведем краткий ликбез по теории вероятностей.
В этом разделе математики оценивается вероятность наступления разных событий. Также можно говорить о вероятности того, что какая-то величина принимает определенное значение. Вероятность наступления события $A$ обозначается так: $P(A)$. Важно понимать, что вероятность - это величина, всегда лежащая в интервале $[0; 1]$. То есть вероятность не может быть отрицательной или быть больше единицы. Событие, вероятность которого равна 0, называют невозможным. А если вероятность равна 1, то такое называют достоверным событием. Например, если $A$ - это выпадение орла, а $B$ - это выпадение решки при подбрасывании монеты, то можно оценить вероятности этих событий так: $P(A) = 0.5; P(B) = 0.5$. В таком случае, подбрасывание монетки это события - а орел или решка - два возможных исхода этого события.
В статистике важно понимать, как интерпретируется сумма и произведение вероятностей. Сумма вероятностей имеет смысл, если события, которые мы складываем “несовместные”, то есть не могут произойти одновременно. Тогда сумма их вероятностей будет являться вероятностью того, что произойдет хотя бы одно из них. В нашем примере с монеткой: $P(A) + P(B) = 0.5 + 0.5 = 1 = P(A+B)$. Обратите внимание, как обозначается такая комбинация событий - мы как бы складываем два события. Это значит “или” - либо одно, либо другое (оба сразу не может быть, так как по определению события несовместные). Про произведение вероятностей скажем чуть позже.
Кроме вероятности определенных событий говорят о вероятности значения определенной случайной величины. Например, если мы подбрасываем кубик, то значение, выпавшее на нем, можно рассматривать как случайную величину. То есть это некоторая величина, переменна, значение которой определяется случайно и разные значения могут иметь разную вероятность (а могут и одну). Обозначают вероятность определенного значения величины так: $P(a=1) = \frac{1}{6}$. То есть, вероятность выпадения единицы (другими словами, того, что значением данной случайной величины станет единица) равна одной шестой. И это интуитивно понятно - всего у нас шесть возможных исходов (событий), причем все они равновероятны (предполагаем, что кубик “честный”). Причем вероятность того, что кубик выпадет хоть какой-то стороной (полная вероятность) равна, очевидно, единице. Отсюда вероятность каждого конкретного значения равна одной шестой.
Это очень важный момент. Как оценить вероятность какого-то события или величины, если про нее заранее ничего не известно? Нужно разбить данный исход как комбинацию равновероятных несовместных событий из определенного набора, причем события в данном наборе должны покрывать все возможные исходы. Таким образом по правилу суммы вероятностей, она будет равна единице. А отсюда уже можно легко вычислить вероятность каждого конкретного исхода. Именно так мы рассуждали в случае с кубиком, точно также получается вероятность 50% для подбрасывания монетки.
Произведение вероятностей носит другой смысл. Оно имеет смысл, если мы говорим о независимых событиях. Независимыми событиями называются такие, которые не влияют друг на друга. То есть исход одного события не изменяет вероятности исхода другого события. Независимость событий - очень важное понятие в теории вероятностей, и мы им будем тоже часто пользоваться. Иногда зависимость или независимость двух событий просто предполагают, иногда - оценивают с помощью данных (мы поговорим, как), а иногда это понятно из контекста. Но в любом случае, если два события независимы, то вероятность их комбинации, то есть того, что они произойдут одновременно, равна произведению вероятностей. Так, если мы кидаем два кубика независимо друг от друга, то вероятность того, что выпадут две шестерки равна: $P(a=6, b=6) = P(a=6) \cdot P(b=6) = \frac{1}{36}$. И опять, обратите внимание, как обозначается комбинация двух независимых событий: $P(A, B)$ - обозначает вероятность того, что и $A$ и $B$ произойдут одновременно. Такая же вероятность будет у любой другой конкретной комбинации выпадения двух кубиков.
Не всегда определение вероятностей может быть таким простым. Но в большинстве случаев, правила произведения и суммы дают шанс вычислить вероятности каких-то более сложных событий и величин. Представим например, опять подбрасывание двух кубиков. Но на этот раз зададим вопрос: какова вероятность того, что их сумма составит, например, десять? Для расчета этой вероятности нужно исходить из равновероятных событий. Как мы уже знаем, каждая конкретная комбинация значений двух кубиков имеет равную вероятность $\frac{1}{36}$. Из этих 36 равновероятных исходов сумму, равную десяти, дают три: (4,6), (5,5), (6,4). Причем все они являются несовместными. Отсюда получаем, что $P(S=9) = \frac{1}{36} + \frac{1}{36} + \frac{1}{36} = \frac{3}{36} = \frac{1}{13}$. Обратите внимание, что мы можем просто умножить базовую вероятность каждого исхода на количество таких исходов, которые дают нужный нам результат. Поэтому, например, $P(S=2) = \frac{1}{36}$, так как всего одна комбинация дает такое значение суммы.
Если мы говорим о случайной величине, можно рассматривать $P(S)$ как функцию, зависящую от значения случайной величины: $P(S) = P(S)(x) = P(S = x)$. Такую функцию называют распределение случайной величины.
А что делать, если события или значения не являются независимыми? В таком случае говорят об условной вероятности. Условная вероятность - это еще одно фундаментальное понятие теории вероятностей и математической статистики. Она обозначается $P(A \mid B)$ - вероятность события $A$ при условии, что наступило событие $B$. Обратите внимание, что в этой вероятности сами события играют разную роль. Первое - до вертикальной черты - это событие, вероятность которого мы хотим найти. А второе - после черты - мы предполагаем, что оно уже произошло. Поэтому, например, $P(A|A) = 1$ всегда - вероятность события, которые уже произошло, равна 100%.
Зависимость в теории вероятностей - исключительно числовое понятие. Как мы говорили раньше, два события независимы, если исход одного из них не меняет вероятности другого. Это можно записать так: $P(A|B) = P(A)$. то есть вероятность события $A$ всегда одна и та же, предполагаем ли мы наступление события $B$ или нет. Зависимость же определяется так: если исход одного события (или значение одной случайной величины) влияет на вероятность исхода второго (или на распределение вероятности второй случайной величины), то второе событие зависит от первого. Или в виде формулы: $P(A|B) \ne P(A)$.
Если у нас есть две случайные величины, их взаимозависимость часто изображают на графике - вероятностной графовой модели. Причем, в теории вероятностей, в отличие от математической статистики, обычно говорят именно о направленных зависимостях. То есть, если $A$ зависит от $B$, то это не гарантирует того, что $B$ зависит от $A$. Например, результат медицинского теста зависит от наличия у пациента болезни, но наличие болезни не зависит от результата теста. Если предполагается, что величина $B$ зависит от величины $A$, то это изображается так:
Для величин, зависящих друг от друга, правило произведения уже не действует. Вернее, оно имеет другой, более полный вид: $P(A, B) = P(A \mid B) \cdot P(B)$. Если подставить в эту формулу условие независимости событий, она сведется к уже рассмотренному правилу суммы. Эта формула более универсальна - ее можно применять как для зависимых, так и независимых событий. Вообще, в теории вероятностей, независимость событий или величин сильно упрощает все расчеты, но ее следует отдельно доказывать, а по умолчанию лучше предполагать, что события зависимы.
Условная вероятность учитывает, что между некоторыми событиями может существовать причинно-следственная связь. И в зависимости от конкретных причин, данное событие может иметь разную вероятность. Вероятность события $P(A)$ всегда предполагает, что мы вычисляем вероятность событие вне зависимости от всех возможных причин. Такая вероятность называется априорной. А если мы знаем причину, то есть исход события $B$, то мы можем вычислить вероятность события $A$ уже с учетом этого знания. Такая вероятность называется апостериорной, то есть полученной на основании полученного опыта (знания о $B$).
Связывает априорную и апостериорную вероятности так называемая формула полной вероятности:
\[P(A) = \sum_{i=1}^n P(A \mid B=b_i) \cdot P(B=b_i)\]В этой формуле $b_i$ - это разные возможные значения $B$ (исходы события или значения величины), которое влияет на $A$. Фактически, эта формула является комбинацией уже знакомых нам правил суммы и произведения. Простыми словами - чтобы вычислить полную вероятность какого-то события нужно сложить вероятности этого события при условии всех возможных причин, умноженных на вероятности самих этих причин.
С условной вероятностью связано много непонимания и заблуждений. Самое главное из них в том, что люди, не знакомые со статистикой и теорией вероятностей, обычно предполагают, что $P(A|B) = P(B|A)$, хотя обычно это совсем не так. Например, рассмотрим медицинский тест для выявления какой-то редкой болезни. Допустим, болезнь встречается один раз в тысячу случаев. При это тест имеет 90%-ю эффективность. То есть, Если болезнь у пациента есть, то тест покажет положительный результат только в 90% случаев, а в остальных 10% ошибется. И наоборот, если болезни нет, сохраняется 10%-й шанс того, что тест покажет все-таки положительный результат Вопрос: тест показал положительный результат, какова вероятность, что пациент болен?
Многие думают, что ответ - 90%. Но это совсем не так, в реальности она гораздо ниже. Дело в том, что в задаче и в вопросе говорится о разных величинах. Обозначим событие наличия болезни - $D$ со значениями 0 или 1. $D = 1$, соответственно, означает, что болезнь есть. А событие проведение теста - $T$. Соответственно, $T = 1$ означает, что тест показал положительный результат. Таким образом, в условии задачи нам дана такая вероятность: $P(T \mid D)$, а в вопросе говорится о такой: $P(D \mid T)$ или более конкретно - $P(D=1 \mid T=1)$. Вероятности поменялись местами. И разница здесь значительна - вероятность болезни при условии известного результата теста, либо вероятность получить определенный результат при условии, что известно наличие или отсутствие болезни.
Так как же считать такие вероятности? Для этого и нужна формула Байеса - одна из основных и самых известных формул теории вероятностей:
Эта формула как раз и позволяет “перевернуть” события в формуле условной вероятности - поменять местами причину и следствие, вычислить точную вероятность события, по факту знания о его причинах. Давайте посмотрим, как формула Байеса применима к задаче про медицинский тест:
\[P(D=1 \mid T=1) = \frac{P(T=1 \mid D=1) \cdot P(D=1)}{P(T=1)}\]Вероятность $P(T=1 \mid D=1)$ мы знаем - она дана в условии задаче и равна 0,1. Это вероятность ошибки теста. Вероятность $P(D=1)$ мы тоже знаем из условия - 0,001. А вот вероятность $P(D=1)$ нам в явном виде не дана, ее надо вычислить. Это априорная вероятность получения положительного результата теста (без учета, есть болезнь или нет). Так как нужно вычислить априорную вероятность по известным апостериорным, нам поможет в этом формула полной вероятности:
\[P(D=1) = \sum P(T=1 \mid D) \cdot P(D) = \\ P(T=1 \mid D=1) \cdot P(D=1) + P(T=1 \mid D=0) \cdot P(D=0) = \\ 0.9 \cdot 0.001 + 0.1 \cdot 0.999 = 0.009 + 0.0999 = 0.1089 \approx 0.1\]То есть вероятность получения положительного результата тест равна примерно 10%, что интуитивно достаточно понятно. Но давайте теперь подставим полученные данные в формулу Байеса:
\[P(D=1 \mid T=1) = \frac{P(T=1 \mid D=1) \cdot P(D=1)}{P(T=1)} = \frac{0.9 \cdot 0.001}{0.1} = 0.09\]Вероятность, что у пациента действительно есть эта болезнь составляет всего 9%, и это при условии, что он получил положительный результат теста. Интуитивно данный результат можно понять так: точность теста с лихвой компенсируется редкостью болезни. Так что с условными вероятностями надо быть очень аккуратными и не предполагать результат из общего “здравого смысла”.
Но вернемся к задаче машинного обучения.
В ней мы оцениваем значение целевой переменной. Наивный байесовский классификатор будет оценивать вероятность каждого возможного значения целевой переменной при условии известных значений признаков. Естественно, и целевая переменная и признаки представляются в этой модели как случайные величины. Причем, признаки влияют на целевую переменную. В терминах теории вероятностей это значит, что при разных значениях признаков вероятности целевой переменной будут другими. В результате оценки классификатор выбирает для предсказания то значение целевой переменной (класс), который имеет наибольшую вероятность при известных значениях признака.
В данном случае целевая переменная выступает в роли случайной величины, вероятность которой мы исследуем, а факторы - это причины. Для каждого объекта, для которого мы делаем предсказание, мы знаем значение факторов и по ним хотим найти распределение вероятности значений целевой переменной. То есть нас интересует величина $P(y \mid \vec{x})$ - условная вероятность целевой переменной при известных значениях признаков. Она же - апостериорная вероятность класса (апостериорная - потому, что мы знаем значение причинных факторов). Так как признаков в общем случае может быть много, то эта величина записывается так: $P(y \mid x_1, x_2, … x_n)$ - вероятность результата, при условии, что мы знаем одновременно значения каждой факторной переменной. По формуле Байеса эта величина может быть рассчитана так:
Давайте разбираться, какие величины нам нужны, чтобы рассчитать нужную нам вероятность. $P(y)$ - это распределение вероятностей различных значений целевой переменной. Она же - априорная вероятность данного класса. Как нам найти ее? В математической статистике принят такой метод: если мы не знаем истинную вероятность события, то ее можно аппроксимировать частотой этого события в некоторой выборке.
Так, например, вероятность выпадения орла при подбрасывании монетки можно определить теоретически (как мы делали выше) - через предположение о равновероятности каких-то событий. А что если мы не можем сделать такое предположение? Вероятность можно оценить и эмпирически - из опыта. Подбросим монетку 10 раз и подсчитаем долю случаев, когда выпал орел. Эта доля будет оценкой вероятности выпадения орла.
Как можно заметить, эта доля не всегда будет равна точно 0,5. Если подбросить монетку 10 раз, от орел вполне может выпасть, скажем, всего 3 раза. Это же неправильно? Да, именно поэтому мы неопределяем вероятность как долю, а именно приближаем ее. То есть такой эмпирический способ может нам дать всего-лишь некоторый ориентир. Причем, чем больше будет наша выборка, тем скорее оценка будет приближаться к истинной вероятности. Если, например, подбросить монетку 100 раз, то очень вряд ли только 300 выпадений придется на орла. Скорее где-то между 450 и 550, что даст нам оценку вероятности 0,45 - 0,55 А если провести миллион экспериментов, то оценка вероятности будет еще точнее и надежнее.
В машинном обучении у нас как раз есть такой источник информации для эмпирической оценки вероятностей через частоты - обучающая выборка. То есть мы оцениваем распределение вероятности каждого значения целевой переменной просто подсчитывая долю тех или иных значений в обучающем наборе данных. точно также оцениваются и другие вероятности. И поэтому исходя из замечания выше, чем больше у нас обучающая выборка, тем ближе и точнее такие эмпирические оценки будут к истинным значениям вероятностей и тем точнее и надежнее будет работать наш классификатор.
Продолжим. Следующая величина - $P(x_1, x_2, … x_n \mid y)$ - вероятность признаков при данном классе. По сути это условная вероятность комбинации значений факторов. Оценивать ее непосредственно очень сложно. Поэтому мы воспользуемся правилом произведения, чтобы привести эту величину к более простому виду. Вот здесь кроется небольшой подвох. Если использовать полный вид правила произведения, мы сделаем только хуже, ведь оно приведет к увеличению количества условных вероятностей и легче не станет. Поэтому мы сделаем предположение о независимости факторных величин, то есть признаков.
Именно из-за этого предположения данная модель называется наивной - она наивно полагает, что все признаки попарно полностью независимы друг от друга. На практике это зачастую не так или не совсем так. Но наивный байесовский классификатор благодаря этому допущению очень прост в своей работе. И зачастую зависимостью признаков между собой действительно можно пренебречь.
Итак, если мы убедим себя в независимости признаков, то данная величина преобразуется так:
\[P(x_1, x_2, ... x_n \mid y) = P(x_1 \mid y) \cdot P(x_1 \mid y) \cdot ... \cdot P(x_n \mid y) = \prod_{i=1}^n P(x_i \mid y)\]то есть это просто произведение вероятности значения каждого признака при данном значении класса. А эта величина оценивается как частота наблюдения данного значения признака при данном значении класса в обучающей выборке. Обратите внимание, что условные вероятности рассчитываются как условные же частоты. То есть мы смотрим на частоту появления данного значения не во всей выборке, а только среди тех точек, в которых наблюдается нужное значение целевой переменной.
С величиной $P(x_1, x_2, …, x_n)$ все еще проще - мы так же применяем правило произведения и получаем $\prod_{i=1}^n P(x_i)$, то есть безусловную вероятность нахождения данного значения каждого признака во всей обучающей выборке. Таким образом, мы будем использовать вот такую форму правила Байеса для расчетов:
И еще напомним, что запись $P(y)$, где $y$ - это случайная величина означает распределение вероятностей, то есть вектор вероятностей для всех значений этой случайно величины. То есть нам надо рассчитать $P(y = y_1), P(y = y_2), … P(y = y_k)$, $y_i$ - это конкретное значение целевой переменной. Другими словами мы рассчитываем по формуле выше вероятности для каждого класса, а затем выбираем такой класс, для которого получившаяся вероятность максимальна:
\[y = argmax_j \frac{P(y=y_j) \cdot \prod_{i=1}^n P(x_i \mid y=y_j)}{\prod_{i=1}^n P(x_i)}\]Вот и весь алгоритм наивного Байесовского классификатора. Для лучшего понимания проиллюстрирует его работу на простом примере. Допустим, у нас есть такая выборка:
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| a | 1 | p |
| b | 1 | p |
| a | 2 | p |
| b | 1 | t |
| c | 2 | t |
| c | 1 | ? |
Первые пять строчек - это обучающая выборка, а последняя - объект, который нам нужно классифицировать. Можно заметить, что целевая переменная $y$ здесь принимает всего два значения - p и t. Значит нам нужно посчитать вероятности двух значений целевой переменной при известных значениях признаков: $P(y=p \mid x_1=c, x_2=1 )$ и $P(y=t \mid x_1=c, x_2=1 )$. Обратите внимание, что нам для классификации данного объекта будут нужны только вероятности тех значений признаков, которые имеет интересующий нас объект (в данном случае, $x_1=c$ и $x_2=1$). Нам не интересны случаи, когда $x_1=a$ или $x_2=2$. Но для классификации произвольных объектов, классификатор должен запоминать априорные и апостериорные вероятности всех значений всех признаков.
Для вычисления первой вероятности применим формулу Байеса:
\[P(y=p \mid x_1=c, x_2=1) = \frac{P(y=p) \cdot P(x_1=c \mid y=p) \cdot P(x_2=1 \mid y=p)}{P(x_1=c) \cdot P(x_2=1)}\]Начнем по порядку. $P(y=p)$ - это доля объектов обучающей выборки, для которых $y=p$. У нас таких 3 из пяти, соответственно, вероятность оцениваем как 0,6. $P(x_1=c \mid y=p)$ - доля объектов, у которых $x_1=c$ среди объектов у которых $y=p$. В обучающей выборке таких нет, значит вероятность равна нулю. Аналогично $P(x_2=1 \mid y=p)$ - таких объектов 2 из трех, вероятность равна 2/3. Ну и безусловные вероятности значений признаков. $P(x_1=c)$ равна 1/5, так как только один объект обучающей выборки имеет такое значение первого признака, а $P(x_2=1)$ равна 3/5 или 0,6, так как таких объектов два из пяти. Подставив значения получаем:
\[P(y=p \mid x_1=c, x_2=1) = \frac{0,6 \cdot 0 \cdot 0,67}{0,2 \cdot 0,6} = 0\]Получаем, что объект с такими значениями признаков вообще не может иметь данный класс. Это объяснимо тем, что в обучающей выборке нет ни одного объекта с первым признаком равным $c$, который принадлежал бы классу $p$. Давайте рассчитаем вероятность второго класса:
\[P(y=t \mid x_1=c, x_2=1) = \frac{P(y=t) \cdot P(x_1=c \mid y=t) \cdot P(x_2=1 \mid y=t)}{P(x_1=c) \cdot P(x_2=1)} = \frac{0,4 \cdot 0,5 \cdot 0,5}{0,2 \cdot 0,6} \approx 0.83\]Получаем довольно большую вероятность того, что данный объект принадлежит классу $t$. Обратите внимание, что для одного объекта знаменатели в расчетах для двух классов полностью идентичны. Это логично, так как знаменатель в формуле Байеса не зависит от значения целевой переменной. Поэтому в реальных расчетах рассчитывают только числитель и выбирают тот класс, в котором числитель максимален:
\[y = argmax_j P(y=y_j) \cdot \prod_{i=1}^n P(x_i \mid y=y_j)\]Наивный Байесовский классификатор прекрасно работает во многих практических задачах, несмотря на свою простоту и нетребовательность к вычислительным мощностям. Параметрами данной модели будут являться рассчитанные оценки условных и априорных вероятностей всех значений признаков и целевой переменной. Поэтому собственно подбора параметров в итеративном процессе не происходит, байесовский классификатор учится очень быстро. При этом, в отличие от метода ближайших соседей ему не нужно для предсказания хранить в памяти всю обучающую выборку.
Метод наивного Байеса, как еще называют эту модель прекрасно работает с категориальными данными и не очень требователен к очистке и преобразованию данных. Для его корректной работы не нужно преобразовывать категориальные переменные в численные (про это пойдет речь в следующих главах). При этом он может менее эффективно работать с данными, в которых множество численных значений.
Пока мы говорили и приводили примеры только категориальных переменных, то есть таких, которые принимают значения из конечного дискретного набора. В нашем примере такими были оба признака. Но на практике встречаются и численные признаки. Неужели для работы байесовского классификатора нужно подсчитывать частоты каждого возможного значения?
Конечно нет. Для оценки вероятности непрерывной величины используется нормальное распределение. Это одно из самых распространенных непрерывных распределений в статистике, поэтому его использование довольно оправдано. И то приятно, для его оценки нужно всего два параметра: математическое ожидание и среднеквадратическое отклонение. Математическое ожидание ($\mu$) оценивается просто как выборочное среднее, то есть среднее арифметическое всех значений данного признака в обучающей выборке. Среднеквадратическое отклонение ($\sigma$) оценивается как квадратный корень из среднего квадрата отклонения значений от среднего: $\sigma = \sqrt{\frac{1}{n - 1} \sum_{i=1}^n (x_i - \mu)^2}$.
С помощью этих двух параметров можно задать функцию плотности вероятности случайной величины как функцию Гаусса:
\[P(x) = \frac{1}{\sigma \sqrt{2 \pi}} e^{- \frac{1}{2} (\frac{x - \mu}{\sigma})^2}\]Эта функция задает распределение характерного вида, которое похоже на колоколообразную кривую:
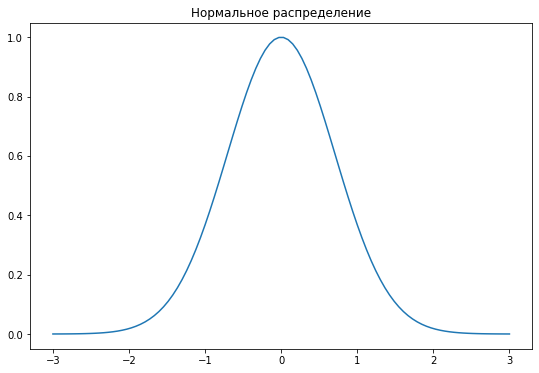
Нормальное распределение подразумевает, что значение данной случайной величины вероятнее будет близко к среднему значению. Чем дальше от среднего, тем меньше вероятность наблюдать это значение. Очень многие величины в реальной жизни распределены по данному статистическому закону. Но существуют и некоторые переменные, распределение которых сильно отличается от нормального. В принципе, в наивном байесовском классификаторе можно использовать и другие формы распределения, но в подавляющем большинстве случаев используется именно нормальное или гауссово распределение.
Приведем пример использования наивного байесовского классификатора с использованием библиотечных функций. Создание и обучение такой модели ничем неотличается от других:
1
2
from sklearn.naive_bayes import GaussianNB
clf = GaussianNB()
Обратите внимание, что мы будем использовать именно вариант классификатора, который использует нормальное распределение, так как в наших данных присутствуют непрерывные признаки. Байесовский классификатор генерирует довольно оригинальную форму границы принятия решения за счет того, что он использует многомерное нормальное распределение:
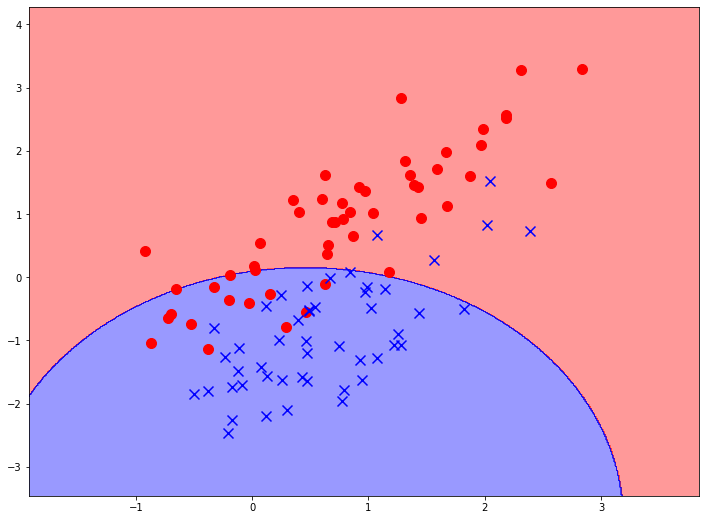
Несомненным достоинством этой модели является то, что она может показывать очень адекватные результаты на малых наборах данных. Ведь если выборка собрана репрезентативная и в ней мало непоказательных объектов, частоты различных значений довольно быстро приближаются к истинным значениям соответствующих вероятностей. За счет этого наивный Байес гораздо меньше подвержен переобучению, чем другие модели, при аналогичном количестве данных и параметров модели.
Наивный байесовский классификатор имеет и ряд существенных недостатков, которые ограничивают его применение. Как мы уже говорили, если в данных присутствуют непрерывные признаки, то эффективность его работы напрямую зависит от формы их распределения, чаще всего от того, насколько она отличается от нормальной.
Кроме того, как мы уже видели на примере, если каке-то конкретное значение не встречается в обучающей выборке (или в ее определенной части для условных вероятностей), это приводит к тому, что соответствующая вероятность будет оценена как ноль. Если эта вероятность в числителе это приведет к тому, что вся апостериорная вероятность обратится в ноль, несмотря на значение других вероятностей, входящих в расчет. Если же эта вероятность будет в знаменателе, результатом будет неопределенность. Чтобы избавится от этого недостатка частоты очень часто сглаживают. То есть рассчитывают не по формуле $\frac{a}{b}$, где $a$ - количество объектов, обладающих определенным значением, $b$ - общее количество значений, а по формуле $\frac{a+1}{b+1}$. В таком случае вероятности не могут обратится в ноль никогда. Эта техника называется оценкой Лапласа или сглаживанием Лапласа.
Традиционной сферой применения наивных байесовских классификаторов является классификация и рубрикация текстовых данных. Наивный Байес хорошо показывает себя в задачах определения тональности текста, отнесения текстов к определенным темам. Также этот алгоритм легко справляется с задачами многоклассовой классификации. За счет своей быстрой работы (предсказание сводится к простому умножению нескольких чисел и выбору максимума) он может использоваться там, где нужно предсказание в режиме реального времени и скорость работы алгоритма критична.
Выводы:
- Наивный байесовский классификатор - модель, основанная на применении формулы Байеса.
- Этот метод полагается на предположение о независимости признаков.
- Хорошо обучается на малых наборах данных.
- Наивные байесовские классификаторы очень быстро работают.
- Все параметры классификатора могут быть аппроксимированы относительными частотами из обучающей выборки.
- Непрерывные величины обычно аппроксимируются нормальным распределением.
- Если какое-то значение не встречается в обучающей выборке, то его вероятность будет равна нулю и даст некорректную классификацию.
- Алгоритм чаще всего применяется при анализе текстов - рубрикация, определение тональности, фильтрация спама.
- Эффективность можно сильно повысить при помощи инжиниринга признаков.