Постановка задачи регрессии
Задача регрессии - это один из основных типов моделей машинного обучения. И хотя, большинство задач на практике относятся к другому типу - классификации, мы начнем знакомство с машинным обучением именно с регрессии. Регрессионные модели были известны задолго до появления машинного обучения как отрасли и активно применяются в статистике, эконометрике, математическом моделировании. Машинное обучение предлагает новый взгляд на уже известные в математике модели. И этот новый взгляд позволит строить более сложные и мощные модели, чем классические математические дисциплины.
Задача регрессии относится к категории задач обучения с учителем. Это значит, что набор данных, который используется для обучения, должен иметь определенную структуру. Обычно, датасеты для машинного обучения представляют собой таблицу, в которой по строкам перечислены разные объекты наблюдений или измерений. В столбцах - различные характеристики, или атрибуты, объектов. А на пересечении строк и столбцов - значение данной характеристики у данного объекта. Обычно один атрибут (или переменная) имеет особый характер - именно ее значение мы и хотим научиться предсказывать с помощью модели машинного обучения. Эта характеристика объекта называется целевая переменная. И если эта целевая переменная выражена числом (а точнее, некоторой непрерывной величиной) - то мы говорим о задаче регрессии.
Задача регрессии в машинном обучении - это задача предсказания какой-то численной характеристики объекта предметной области по определенному набору его параметров (атрибутов).
Задачи регрессии на практике встречаются довольно часто. Например, предсказание цены объекта недвижимости - классическая регрессионная задача. В таких проблемах атрибутами выступают разные характеристики квартир или домов - площадь, этажность, расположение, расстояние до центра города, количество комнат, год постройки. В разных наборах данных собрана разная информация И, соответственно, модели тоже должны быть разные. Другой пример - предсказание цены акций или других финансовых активов. Или предсказание температуры завтрашним днем.
Во всех таких задачах нам нужно иметь данные, которые позволят осуществить такое предсказание. Да, “предсказание” - это условный термин, не всегда мы говорим о будущих событиях. Зачастую говорят именно о “моделировании” значения целевой переменной. Регрессионные модели используют информацию об объектах в обучающем наборе данных, чтобы сделать вывод о возможном значении целевой переменной. И для этого нужно, чтобы ее значение имело какую-то зависимость от имеющихся у нас атрибутов. Если построить модель предсказания цены акции, но на вход подать информацию о футбольных матчах - ничего не получится. Мы предполагаем, что в наборе данных собраны именно те атрибуты объектов, которые имеют влияние на на значение целевой переменной. И чем больше это предположение выполняется, тем точнее будет потенциально наша модель.
Немного поговорим о терминах. Набор данных который мы используем для обучения модели называют датасетом (dataset) или обучающей выборкой (training set). Объекты, которые описываются в датасете еще называют точками данных (data points). Целевую переменную еще называют на статистический манер зависимой переменной (dependent variable) или результативной, выходной (output), а остальные атрибуты - независимыми переменными (independent variables), или признаками (features), или факторами, или входными переменными (input). Значения одного конкретного атрибута для всех объектов обучающей выборки часто представляют как вектор этого признака (feature vector). А всю таблицу всех атрибутов называют матрицей атрибутов (feature matrix). Соответственно, еще есть вектор целевой переменной, он не входит в матрицу атрибутов.
Датасет, набор данных - совокупность информации в определенной структурированной форме, которая используется для построения модели машинного обучения для решения определенной задачи. Датасет обычно представляется в табличной форме. Датасет описывает некоторое множество объектов предметной области - точек данных.
С точки зрения информатики, регрессионная модель - это функция, которая принимает на вход значения атрибутов какого-то конкретного объекта и выдает на выходе предполагаемое значение целевой переменной. В большинстве случаев мы предполагаем, что целевая переменная у нас одна. Если стоит задача предсказания нескольких характеристик, то их чаще воспринимают как несколько независимых задач регрессии на одних и тех же атрибутах.
Мы пока ничего не говорили о том, как изнутри устроена регрессионная модель. Это потому, что она может быть какой угодно. Это может быть математическое выражение, условный алгоритм, сложная программа со множеством ветвлений и циклов, нейронная сеть - все это можно представить регрессионной моделью. Единственное требование к модели машинного обучения - она должна быть параметрической. То есть иметь какие-то внутренние параметры, от которых тоже зависит результат вычисления. В простых случаях, чаще всего в качестве регрессионной модели используют аналитические функции. Таких функций бесконечное количество, но чаще всего используется самая простая функция, с которой мы и начнем изучение регрессии - линейная функция.
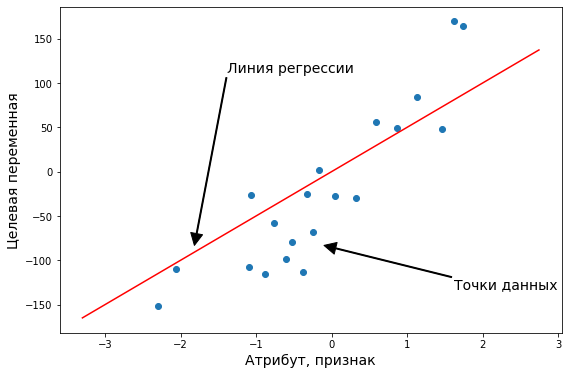
Регрессионные модели подразделяют на парную и множественную регрессии. Парная регрессия - это когда у нас всего один атрибут. Множественная - когда больше одного. Конечно, на практике парная регрессия не встречается, но на примере такой простой модели мы поймем основные концепции машинного обучения. Плюс, парную регрессию очень удобно и наглядно можно изобразить на графике. Когда у нас больше двух переменных, графики уже не особо построишь, и модели приходится визуализировать иначе, более косвенно.
Выводы:
- Регрессия - это задача машинного обучения с учителем, которая заключается в предсказании некоторой непрерывной величины.
- Для использования регрессионных моделей нужно, чтобы в датасете были характеристики объектов и “правильные” значения целевой переменной.
- Примеры регрессионных задач - предсказание цены акции, оценка объекта недвижимости.
- Задача регрессии основывается на предположении, что значение целевой переменной зависит от значения признаков.
- Регрессионная модель принимает набор значений и выдает предсказание значения целевой переменной.
- В качестве регрессионных моделей часто берут аналитические функции, например, линейную.
Парная линейная регрессия
Функция гипотезы
Напомним, что в задачах регрессии мы принимаем входные переменные и пытаемся получить более-менее достоверное значение целевой переменной. Любая функция, даже самая простая линейная может выдавать совершенно разные значения для одних и тех же входных данных, если в функции будут разные параметры. Поэтому, любая регрессионная модель - это не какая-то конкретная математическая функция, а целое семейство функций. И задача алгоритма обучения - подобрать значения параметров таким образом, чтобы для объектов обучающей выборки, для которых мы уже знаем правильные ответы, предсказанные (или теоретические, вычисленные из модели) значения были как можно ближе к тем, которые есть в датасете (эмпирические, истинные значения).
Функция гипотезы - преобразование, которое принимает на вход набор значений признаков определенного объекта и выдает оценку значения целевой переменной данного объекта. Она лежит в основе модели машинного обучения.
Парная, или одномерная (univariate) регрессия используется, когда вы хотите предсказать одно выходное значение (чаще всего обозначаемое $y$), зависящее от одного входного значения (обычно обозначается $x$). Сама функция называется функцией гипотезы или моделью. В качестве функции гипотезы для парной регрессии можно выбрать любую функцию, но мы пока потренируемся с самой простой функцией одной переменной - линейной функцией. Тогда нашу модель можно назвать парной линейной регрессией.
В случае парной линейной регрессии функция гипотезы имеет следующий общий вид:
Обратите внимание, что это похоже на уравнение прямой. Эта модель соответствует множеству всех возможных прямых на плоскости. Когда мы конкретизируем модель значениями параметров (в данном случае - $b_0$ и $b_1$), мы получаем конкретную прямую. И наша задача состоит в том, чтобы выбрать такую прямую, которая бы лучше всего “легла” в точки из нашей обучающей выборки.
В данном случае, мы пытаемся подобрать функцию h(x) таким образом, чтобы отобразить данные нам значения x в данные значения y. Допустим, мы имеем следующий обучающий набор данных:
| Атрибут | Целевая | |
|---|---|---|
| X | Y | |
| Объект 1 | 0 | 4 |
| Объект 2 | 1 | 7 |
| Объект 3 | 2 | 7 |
| Объект 4 | 3 | 8 |
| Объект 5 | 4 | 10 |
| Объект 6 | 5 | 9 |
| Объект 7 | 3 | 9 |
| … | … | … |
| Объект m | $x_m$ | $y_m$ |
Мы можем составить случайную гипотезу с параметрами $ b_0 = 2, b_1 = 2 $. Тогда для входного значения $ x=1 $ модель выдаст предсказание, что $ y=4 $, что на 3 меньше данного. Значение $y$, которое посчитала модель будем называть теоретическим или предсказанным (predicted), а значение, которое дано в наборе данных - эмпирическим или истинным (true). Задача регрессии состоит в нахождении таких параметров функции гипотезы, чтобы она отображала входные значения в выходные как можно более точно (чтобы теоретические значения были как можно ближе к эмпирическим), или, другими словами, описывала линию, наиболее точно ложащуюся в данные точки на плоскости $(x, y)$.
Выводы:
- Модель машинного обучения - это параметрическая функция.
- Задача обучения состоит в том, чтобы подобрать параметры модели таким образом, чтобы она лучше всего описывала обучающие данные.
- Парная линейная регрессия работает, если есть всего одна входящая переменная.
- Парная линейная регрессия - одна из самых простых моделей машинного обучения.
- Парная линейная регрессия соответствует множеству всех прямых на плоскости. Из них мы выбираем одну, наиболее подходящую.
Функция ошибки
Как мы уже говорили, разные значения параметров дают разные конкретные модели. Для того, чтобы подобрать наилучшую модель, нам нужно средство измерения “точности” модели, некоторая функция, которая показывает, насколько модель хорошо или плохо соответствует имеющимся данным.
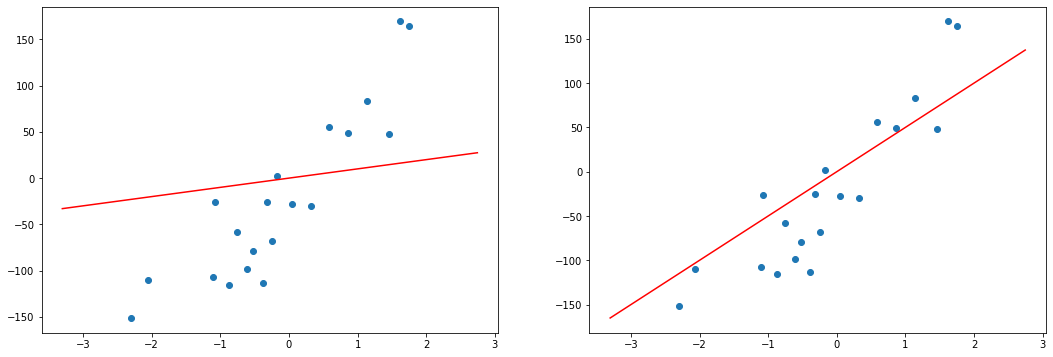
В простых случаях мы можем отличить хорошие модели от плохих, только взглянув на график. Но это затруднительно, если количество признаков очень велико, или если модели лишь немного отличаются друг от друга. Да и для автоматизации процесса нужен способ формализовать наше общее представление о том, что модель “ложится” в точки данных.
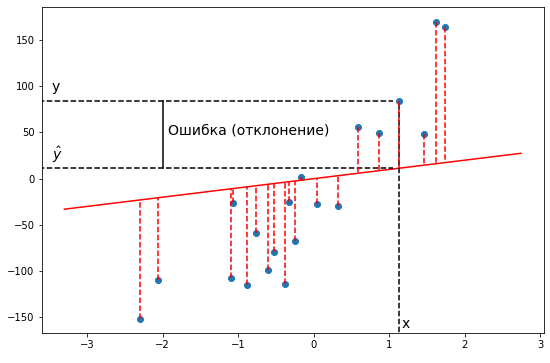
Такая функция называется функцией ошибки (cost function). Она измеряет отклонения теоретических значений (то есть тех, которые предсказывает модель) от эмпирических (то есть тех, которые есть в данных). Чем выше значение функции ошибки, тем хуже модель соответствует имеющимся данным, хуже описывает их. Если модель полностью соответствует данным, то значение функции ошибки будет нулевым.
В задачах регрессии в качестве функции ошибки чаще всего берут среднеквадратичное отклонение теоретических значений от эмпирических. То есть сумму квадратов отклонений, деленную на удвоенное количество измерений. Казалось бы, что это довольно произвольный выбор. Но он вполне обоснован и логичен. Давайте порассуждаем. Чтобы оценить, насколько хороша модель, мы должны оценить, насколько отклоняются эмпирические значения, то есть \(y_i\) от теоретических, предсказанных моделью, то есть \(h_b(x_i)\). Проще всего это отклонение выразить в виде разницы между этими двумя значениями. Но эта разница будет характеризовать отклонение только в одной точке данных, а в датасете может быть их произвольное количество. Поэтому имеет смысл взять сумму этих разностей для всех точек данных:
Но с этим подходом есть одна проблема. Дело в том, что отклонения реальных значений от предсказанных могут быть как положительные, так и отрицательные. И если мы просто их все сложим, то положительные как бы скомпенсируют отрицательные. И в итоге даже очень плохие модели могут выглядеть, как имеющие маленькие ошибки. Фактически, для любого набора данных, если модель проходит через геометрический центр распределения, то такая ошибка будет равна нулю. То есть для достижения нулевой ошибки линии регрессии достаточно проходить через одну определенную точку. Таких моделей, очевидно, бесконечное количество, и все они будут иметь нулевую сумму отклонений. Конечно, так не пойдет и нужно придумать такую формулу, чтобы положительные и отрицательные отклонения не взаимоуничтожались, а складывались без учета знака.
Можно было бы взять отклонения по модулю. Но у такого подхода есть один большой недостаток: Функция абсолютного значения не везде дифференцируема. В одной точке у нее не существует производной. А чуть позже нам очень понадобится брать производную от функции ошибки. Поэтому модуль нам не подходит. Но в математике есть и другие функции, которые позволяют “избавиться” от знака числа. Например, возведение в квадрат. Его как раз и применяют в функции ошибки:
У этого подхода есть еще одно неочевидное достоинство. Квадратичная функция дополнительно сильно увеличивает размер больших чисел. То есть, если среди наших отклонений будет какое-то очень большое, то после возведения в квадрат оно станет еще непропорционально больше. Таким образом квадратичная функция ошибки как бы сильнее “штрафует” сильные отклонения предсказанных значений от реальных.
Но есть еще одна проблема. Дело в том, что в разных наборах данных может быть разное количество точек. Если мы просто будем считать сумму отклонений, то чем больше точек будем суммировать, тем больше итоговое отклонение будет только из-за количества слагаемых. Поэтому модели, обученные на маленьких объемах данных будут иметь преимущество. Это тоже неправильно и поэтому берут не сумму, а среднее из отклонений. Для этого достаточно лишь поделить эту сумму на количество точек данных:
В итоге мы как раз получаем среднеквадратичное отклонение реальных значений от предсказанных. Эта функция дает хорошее представление о том, какая конкретная модель хорошо соответствует имеющимся данным, а какая - хуже или еще лучше.
Эту функцию называют «функцией квадрата ошибки» или «среднеквадратичной ошибкой» (mean squared error, MSE). Среднее значение уменьшено вдвое для удобства вычисления градиентного спуска, так как производная квадратичной функции будет отменять множитель 1/2. Вообще, функцию ошибки можно свободно домножить или разделить на любое число (положительное), ведь нам не важна конкретная величина этой функции. Нам важно, что какие-то модели (то есть наборы значений параметров модели) имеют низкую ошибку, они нам подходят больше, а какие-то - высокую ошибку, они подходят нам меньше.
Обратите внимание, что в качестве аргументов у функции ошибки выступают параметры нашей функции гипотезы. Ведь функция ошибки оценивает отклонение конкретной функции гипотезы (то есть набора значений параметров этой функции) от эмпирических значений, то есть ставит в соответствие каждому набору параметров модели число, характеризующее ошибку этого набора.
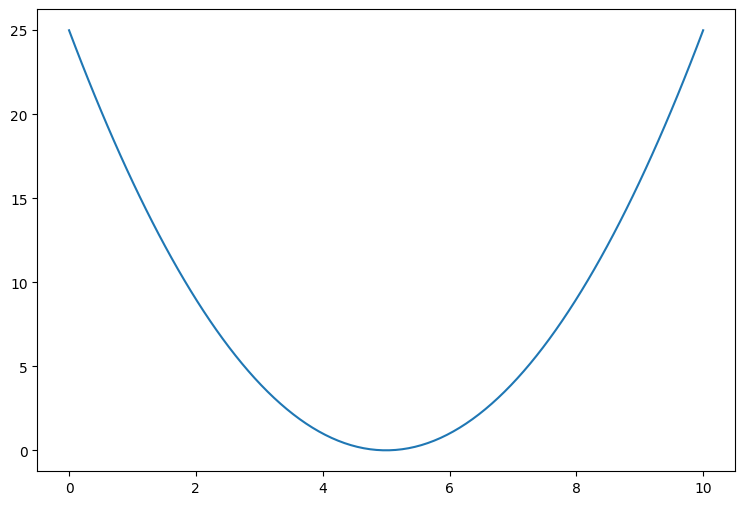
Давайте проследим формирование функции ошибки на еще более простом примере. Возьмем упрощенную форму линейной модели - прямую пропорциональность. Она выражается формулой:
Эта модель поможет нам, так как у нее всего один параметр. И функцию ошибки можно будет изобразить на плоскости. Возьмем фиксированный набор точек и попробуем несколько значений параметра для вычисления функции ошибки. Слева на графике изображены точки данных и текущая функция гипотезы, а на правом графике бы будем отмечать значение использованного параметра (по горизонтали) и получившуюся величину функции ошибки (по вертикали):
При значении $b_1 = -1$ линия существенно отклоняется от точек. Отметим уровень ошибки (примерно 10) на правом графике.
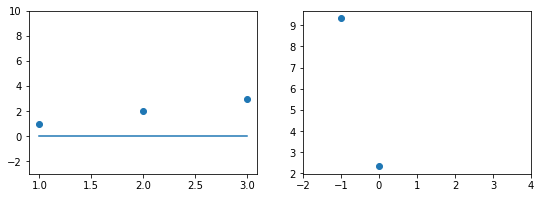
Если взять значение $b_1 = 0$ линия гораздо ближе к точкам, но ошибка все еще есть. Отметим новое значение на правом графике в точке 0.
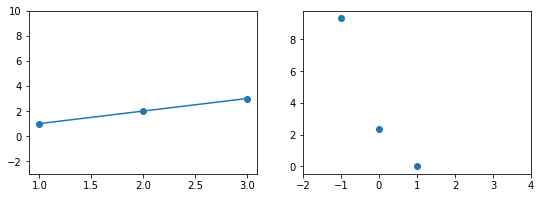
При значении $b_1 = 1$ график точно ложится в точки, таким образом ошибка становится равной нулю. Отмечаем ее так же.
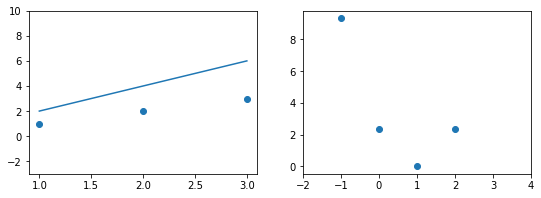
При дальнейшем увеличении $b_1$ линия становится выше точек. Но функция ошибки все равно будет положительной. Теперь она опять станет расти.
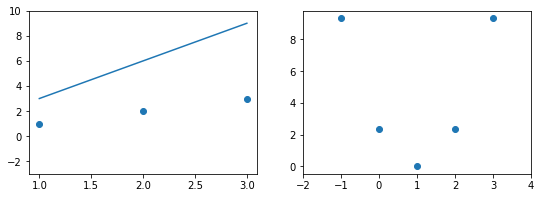
На этом примере мы видим еще одно преимущество возведения в квадрат - это то, что такая функция в простых случаях имеет один глобальный минимум. На правом графике формируется точка за точкой некоторая функция, которая похожа очертаниями на параболу. Но мы не знаем аналитического вида этой параболы, мы можем лишь строить ее точка за точкой.
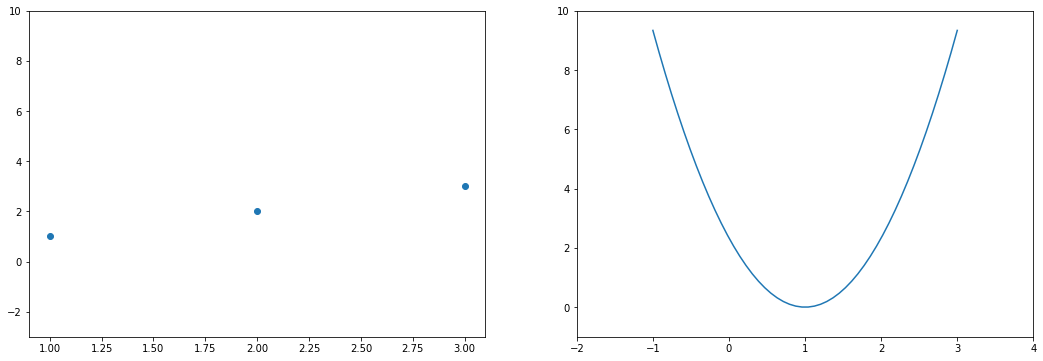
В нашем примере, в определенной точке функция ошибки обращается в ноль. Это соответствует “идеальной” функции гипотезы. То есть такой, когда она проходит четко через все точки. В нашем примере это стало возможно благодаря тому, что точки данных и так располагаются на одной прямой. В общем случае это не выполняется и функция ошибки, вообще говоря, не обязана иметь нули. Но она должна иметь глобальный минимум. Рассмотрим такой неидеальный случай:
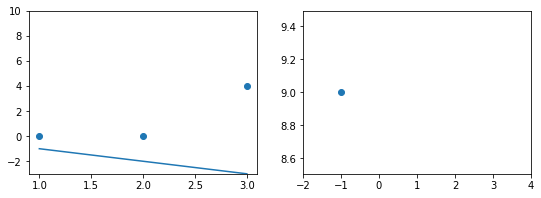
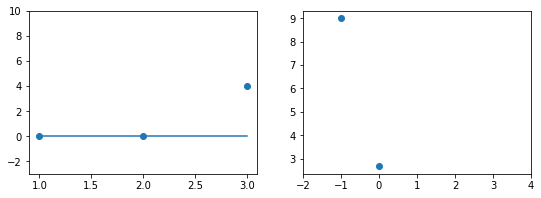
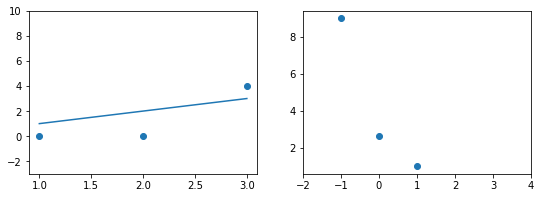
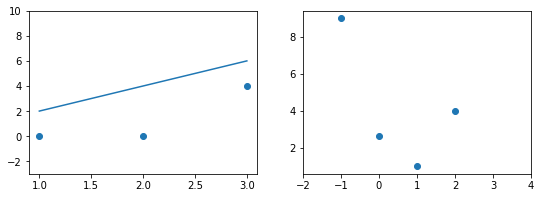
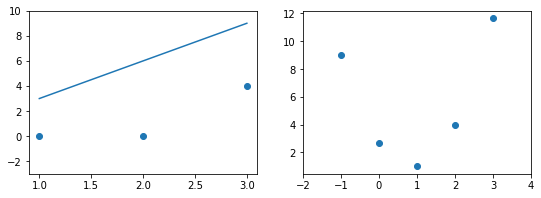
Какое бы значение параметра мы не использовали, линейная функция неспособна идеально пройти через такие три точки, которые не лежат на одной прямой. Эта ситуация называется “недообучение”, об этом мы еще будем говорить дальше. Это значит, что наша модель слишком простая, чтобы идеально описать данные. Но зачастую, идеальная модель и не требуется. Важно лишь найти наилучшую модель из данного класса (например, линейных функций).
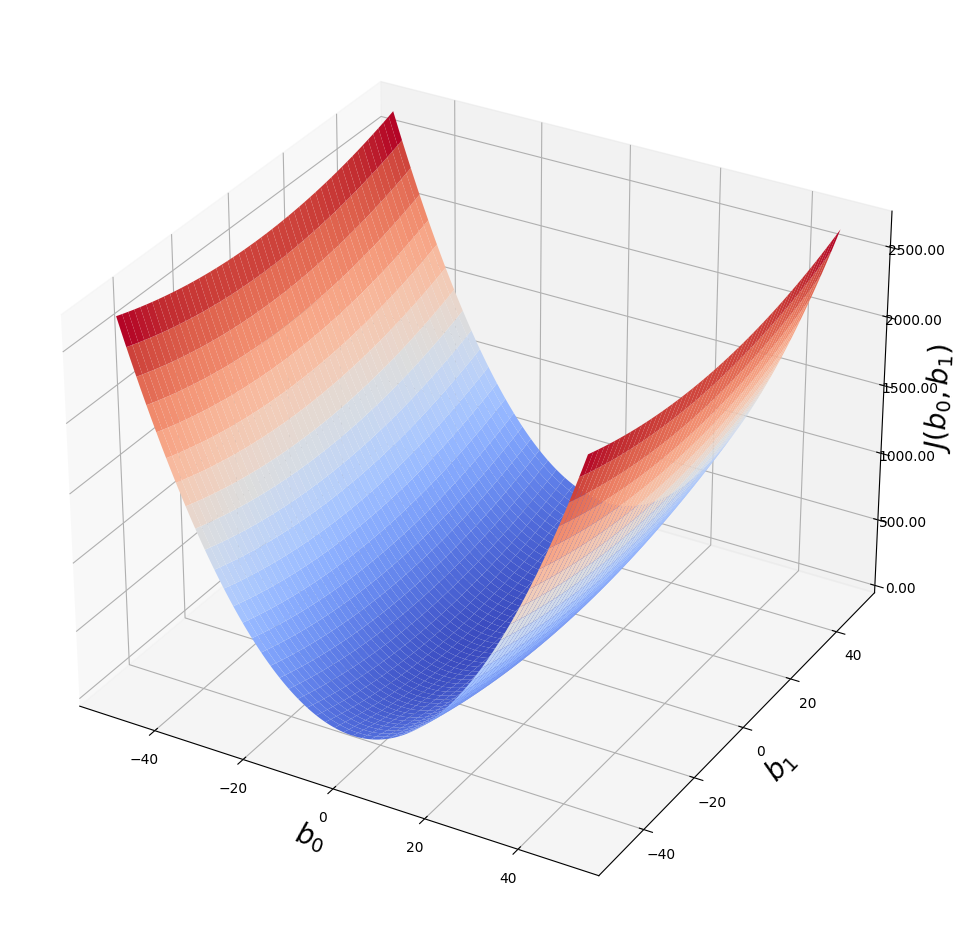
Выше мы рассмотрели упрощенный пример с функцией гипотезы с одним параметром. Но у парной линейной регрессии же два параметра. В таком случае, функция ошибки будет описывать не параболу, а параболоид:
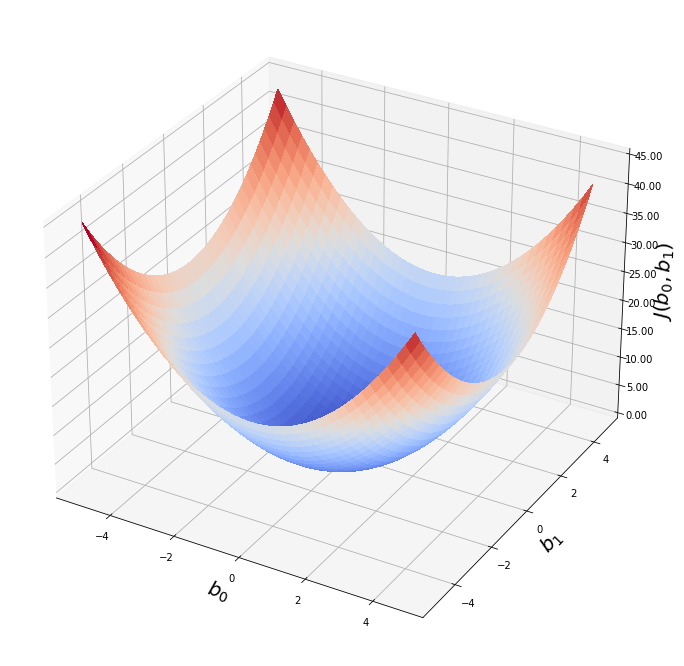
Теперь мы можем конкретно измерить точность нашей предсказывающей функции по сравнению с правильными результатами, которые мы имеем, чтобы мы могли предсказать новые результаты, которых у нас нет.
Если мы попытаемся представить это наглядно, наш набор данных обучения будет разбросан по плоскости x-y. Мы пытаемся подобрать прямую линию, которая проходит через этот разбросанный набор данных. Наша цель - получить наилучшую возможную линию. Лучшая линия будет такой, чтобы средние квадраты вертикальных расстояний точек от линии были наименьшими. В лучшем случае линия должна проходить через все точки нашего набора данных обучения. В таком случае значение J будет равно 0.
В более сложных моделях параметров может быть еще больше, но это не важно, ведь нам не нужно строить функцию ошибки, нам нужно лишь оптимизировать ее.
Выводы:
- Функция ошибки нужна для того, чтобы отличать хорошие модели от плохих.
- Функция ошибки показывает численно, насколько модель хорошо описывает данные.
- Аргументами функции ошибки являются параметры модели, ошибка зависит от них.
- Само значение функции ошибки не несет никакого смысла, оно используется только в сравнении.
- Цель алгоритма машинного обучения - минимизировать функцию ошибки, то есть найти такой набор параметров модели, при которых ошибка минимальна.
- Чаще всего используется так называемая L2-ошибка - средний квадрат отклонений теоретических значений от эмпирических (метрика MSE).
Метод градиентного спуска
Таким образом, у нас есть функция гипотезы, и способ оценить, насколько хорошо конкретная гипотеза вписывается в данные. Теперь нам нужно подобрать параметры функции гипотезы. Вот где приходит на помощь метод градиентного спуска. Идея этого метода достаточно проста, но потребует для детального знакомства вспомнить основы математического анализа и дифференциального исчисления.
Несмотря на то, что мы настоятельно советуем разобраться в основах функционирования метода градиентного спуска шаг за шагом для более полного понимания того, как модели машинного обучения подбирают свои параметры, если читатель совсем не владеет матанализом, данные объяснения можно пропустить, они не являются критичными для повседневного понимания сути моделей машинного обучения.
Это происходит при помощи производной функции ошибки. Напомним, что производная функции показывает направление роста этой функции с ростом аргумента. Необходимое условие минимума функции - обращение в ноль ее производной. А так как мы знаем, что квадратичная функция имеет один глобальный экстремум - минимум, то наша задача очень проста - вычислить производную функции ошибки и найти, где она равна нулю.
Давайте найдем производную среднеквадратической функции ошибки. Так как эта функция зависит от двух аргументов - \(b_0\) и \(b_1\), то нам понадобится взять частные производные этой функции по всем ее аргументам. Для начала вспомним формулу самой функции ошибки:
Частная производная обозначается \(\frac{\partial f}{\partial x}\) или \(\frac{\partial}{\partial x} f\) и является обобщением обычной (полной) производной для функций нескольких аргументов. Частая производная показывает наклон функции в направлении изменения определенного аргумента, то есть как бы “в разрезе” этого аргумента. Градиент - это вектор частных производных функции по всем ее аргументам. Вектор градиента показывает направление максимального роста функции.
Что бы посчитать производную по какому-то из аргументов нам понадобятся обычные правила вычисления производной. Во-первых, общий множитель можно вынести из-под производной, Во-вторых, производная суммы равна сумме производных, поэтому знак суммы тоже можно вынести из-под производной. Поэтому получаем:
Теперь самое сложное - производная сложной функции. По правилу она равна производной внешней функции, умноженной на производную внутренней. Внешняя функция - это квадратическая, ее производная равна удвоенному подквадратному выражению (\(\frac{d}{dt} t^2 = 2 t\)). Подставляем \(t = h_b(x_i) - y^{(i)}\) и получаем:
Обратите внимание, что эта самая двойка прекрасно сократилась со знаменателем в постоянном множителе функции ошибки. Именно за этим он и был нужен.
Чтобы продолжить вычисление производной дальше, нужно представить функцию гипотезы как линейную функцию:
И теперь мы уже не можем говорить о какой-то частной производной в общем, нужно отдельно посчитать производные по разным значениям параметров. Но тут все как раз очень просто, так как нам осталось посчитать производные линейной функции. Они равны просто коэффициентам при соответствующих аргументах. Для свободного коэффициента аргумент равен, очевидно, 1:
А для коэффициента при $x_i$ производная равна самому значению $x_i$:
Теперь для нахождения минимального значения функции ошибки нам нужно только приравнять эти производные к нулю, то есть решить для $b_0, b_1$ следующую систему уравнений:
Проблема в том, что мы не можем просто решить эти уравнения аналитически. Ведь мы не знаем общий вид функции ошибки, не то, что ее производной. Ведь он зависит от всех точек данных. Но мы можем вычислить эту функцию (и ее производную) в любой точке. А точка на этой функции - это конкретный набор значений параметров модели. Поэтому пришлось изобрести численный алгоритм. Он работает следующим образом.
Сначала, мы выбираем произвольное значение параметров модели. То есть, произвольную точку в области определения функции. Мы не знаем, является ли эта точка оптимальной (скорее нет), не знаем, насколько она далека от оптимума. Но мы можем вычислить направление к оптимуму. Ведь мы знаем наклон касательной к графику функции ошибки.
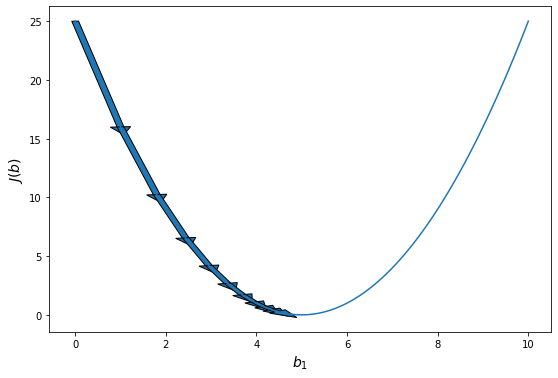
Наклон касательной является производной в этой точке, и это даст нам направление движения в сторону самого крутого уменьшения значения функции. Если представить себе функцию одной переменной (параболу), то там все очень просто. Если производная в точке отрицательна, значит функция убывает, значит, что оптимум находится справа от данной точки. То есть, чтобы приблизиться к оптимуму надо увеличить аргумент функции. Если же производная положительна, то все наоборот - функция возрастает, оптимум находится слева и нам нужно уменьшить значение аргумента. Причем, чем дальше от оптимума, тем быстрее возрастает или убывает функция. То есть значение производной дает нам не только направление, но и величину нужного шага. Сделав шаг, пропорциональный величине производной и в направлении, противоположном ей, можно повторить процесс и еще больше приблизиться к оптимуму. С каждой итерацией мы будем приближаться к минимуму ошибки и математически доказано, что мы можем приблизиться к ней произвольно близко. То есть, данный метод сходится в пределе.
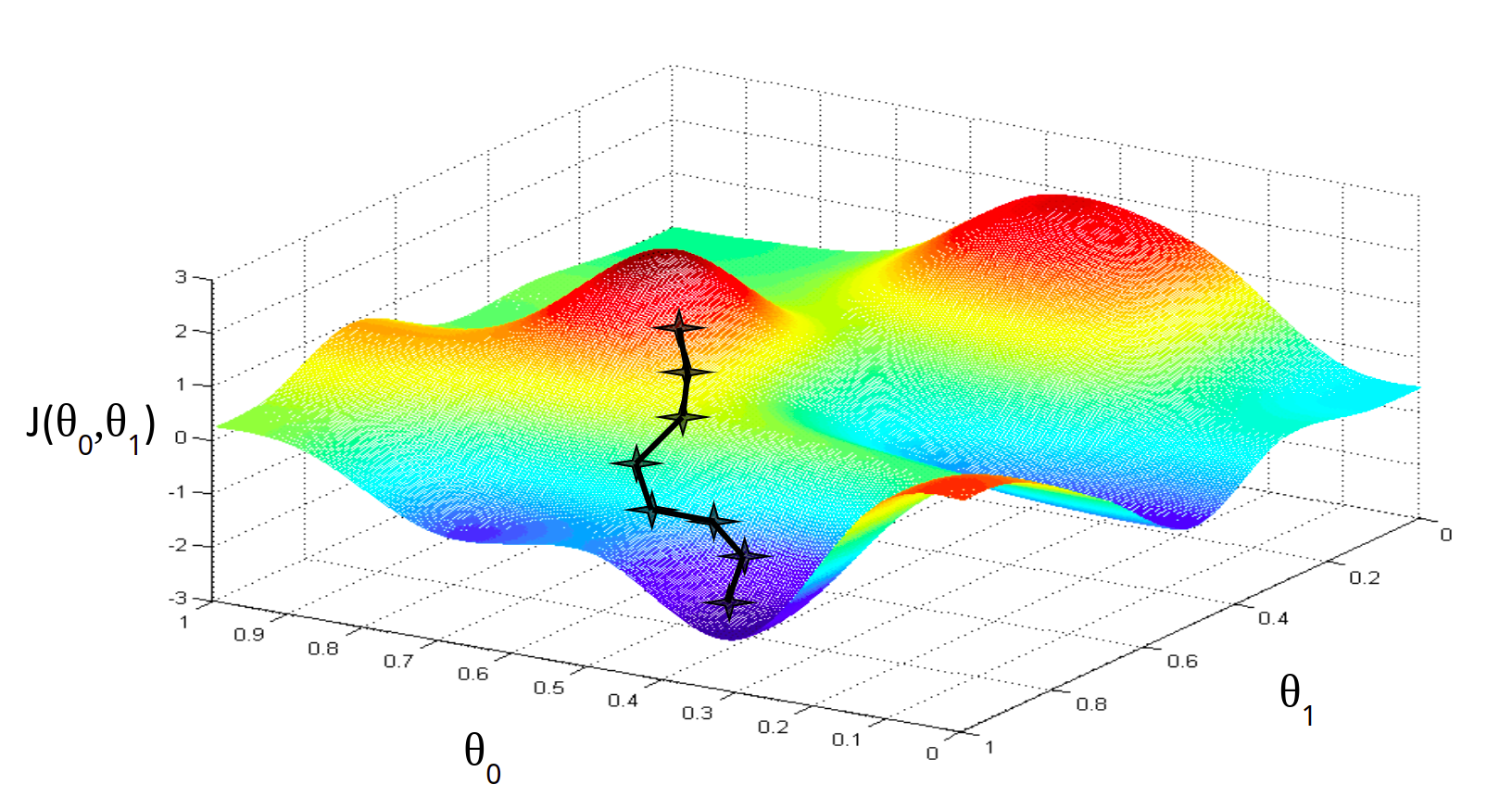
В случае с функцией нескольких переменных все немного сложнее, но принцип остается прежним. Только мы оперируем не полной производной функции, а вектором частных производных по каждому параметру. Он задает нам направление максимального увеличения функции. Чтобы получить направление максимального спада функции нужно просто домножить этот вектор на -1. После этого нужно обновить значения каждого компонента вектора параметров модели на величину, пропорциональную соответствующему компоненту вектора градиента. Таким образом мы делаем шаги вниз по функции ошибки в направлении с самым крутым спуском, а размер каждого шага пропорционален определяется параметром $\alpha$, который называется скоростью обучения.
Алгоритм градиентного спуска:
повторяйте до сходимости:
\[b_j := b_j - \alpha \frac{\partial}{\partial b_j} J(b_0, b_1)\]где j=0,1 - представляет собой индекс номера признака.
Алгоритм градиентного спуска для парной линейной регрессии:
повторяйте до сходимости:
\[b_0 := b_0 - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_b(x_i )- y_i)\] \[b_1 := b_1 - \alpha \frac{1}{m} \sum_{i=1}^{m} \Big( (h_b(x_i) - y_i) \cdot x_i \Big)\]На практике “повторяйте до сходимости” означает, что мы повторяем алгоритм градиентного спуска до тех пор, пока значение функции ошибки не перестанет значимо изменяться. Это будет означать, что мы уже достаточно близко к минимуму и дальнейшие шаги градиентного спуска слишком малы, чтобы быть целесообразными. Конечно, это оценочное суждение, но на практике обычно, нескольких значащих цифр достаточно для практического применения моделей машинного обучения.
Это общий алгоритм градиентного спуска. Она работает для любых моделей и для любых функций ошибки. Это итеративный алгоритм, который сходится в пределе. То есть, мы никогда не придем в сам оптимум, но можем приблизиться к нему сколь угодно близко. На практике нам не так уж важно получить точное решение, достаточно решения с определенной точностью.
Алгоритм градиентного спуска имеет один параметр - скорость обучения. Он влияет на то, как быстро мы будем приближаться к оптимуму. Кажется, что чем быстрее, тем лучше, но оказывается, что если значение данного параметра слишком велико, то мы буем постоянно промахиваться и алгоритм будет расходиться.

Алгоритм градиентного спуска имеет одну особенность, про которую нужно помнить. Он в состоянии находить только локальный минимум функции. Он в принципе, по своей природе, локален. Поэтому, если функция ошибки будет очень сложна и иметь несколько локальных оптимумов, то результат работы градиентного спуска будет зависеть от выбора начальной точки.

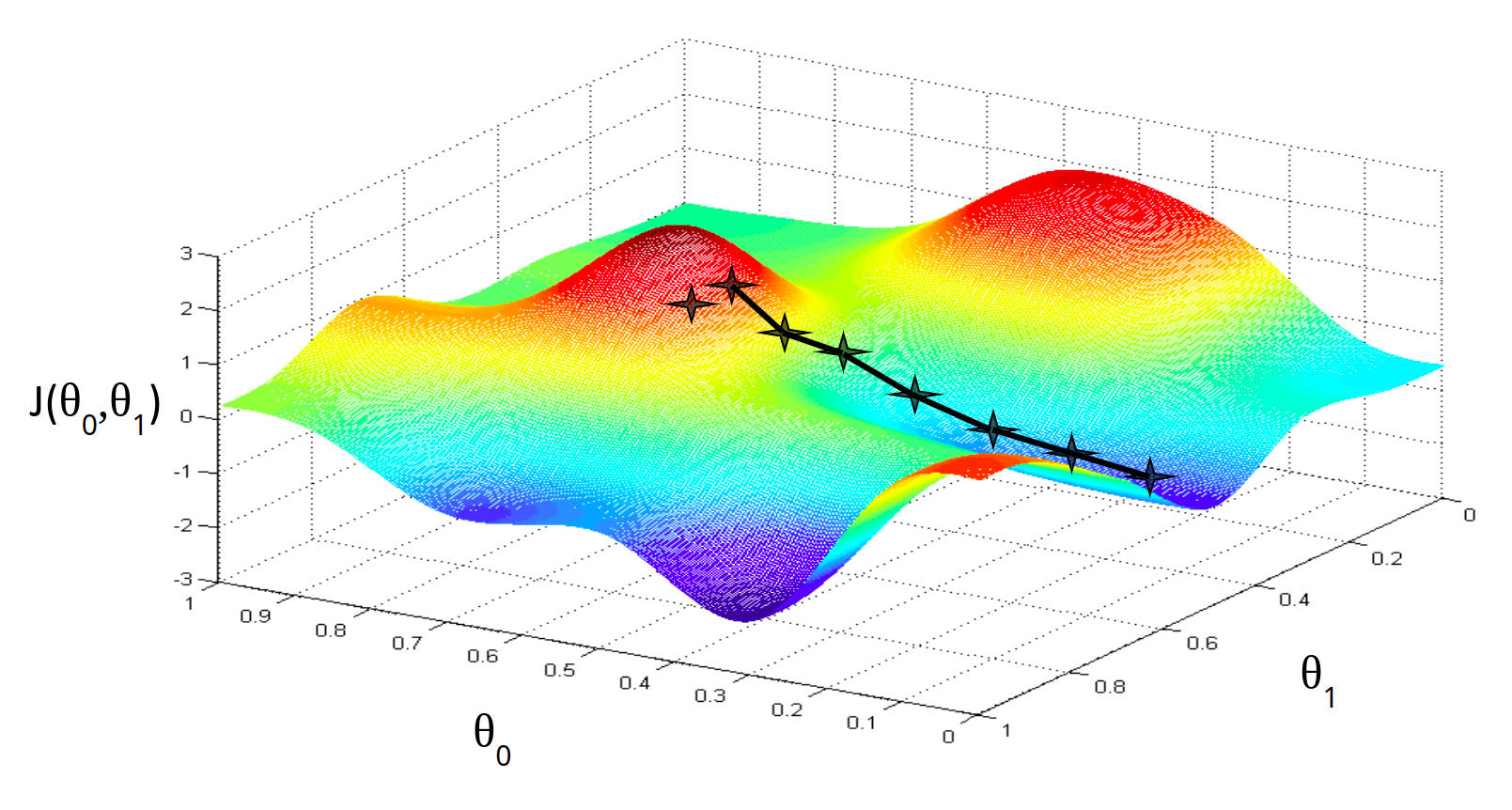
На практике эту проблему решают методом семплирования - запускают градиентный спуск из множества случайных точек и выбирают то минимум, который оказался меньше по значению функции ошибки. Но этот подход понадобится нам при рассмотрении более сложных и глубоких моделей машинного обучения. Для простых линейных, полиномиальных и других моделей метод градиентного спуска работает прекрасно. В настоящее время этот алгоритм - это основная рабочая лошадка классических моделей машинного обучения.
Выводы:
- Метод градиентного спуска нужен, чтобы найти минимум функции, если мы не можем ее вычислить аналитически.
- Это численный итеративный алгоритм локальной оптимизации.
- Для запуска градиентного спуска нужно знать частную производную функции ошибки.
- Для начала мы берем произвольные значения параметров, затем обновляем их по данной формуле.
- Доказано, что этот метод сходится к локальному минимуму.
- Если функция ошибки достаточно сложная, то разные начальные точки дадут разный результат.
- Метод градиентного спуска имеет свой параметр - скорость обучения. Обычно его подстаивают автоматически.
- Метод градиентного спуска повторяют много раз до тех пор, пока функция ошибки не перестанет значимо изменяться.
Регрессия с несколькими переменными
Множественная линейная регрессия
Парная регрессия, как мы увидели выше, имеет дело с объектами, которые характеризуются одним числовым признаком ($x$). На практике, конечно, объекты характеризуются несколькими признаками, а значит в модели должна быть не одна входящая переменная, а несколько (или, что то же самое, вектор). Линейная регрессия с несколькими переменными также известна как «множественная линейная регрессия». Введем обозначения для уравнений, где мы можем иметь любое количество входных переменных:
$ x^{(i)} $- вектор-столбец всех значений признаков i-го обучающего примера;
$ x_j^{(i)} $ - значение j-го признака i-го обучающего примера;
$ x_j $ - вектор j-го признака всех обучающих примеров;
m - количество примеров в обучающей выборке;
n - количество признаков;
X - матрица признаков;
b - вектор параметров регрессии.
| Атрибут 1 | Атрибут 2 | … | Атрибут n | Целевая | |
|---|---|---|---|---|---|
| $x_1$ | $x_2$ | … | $x_n$ | Y | |
| Объект 1 | 0 | 2 | … | 6 | 4 |
| Объект 2 | 1 | 4 | … | 3 | 7 |
| Объект 3 | 2 | 7 | … | 0 | 7 |
| Объект 4 | 3 | 2 | … | 3 | 8 |
| Объект 5 | 4 | 9 | … | 2 | 10 |
| Объект 6 | 5 | 7 | … | 15 | 9 |
| Объект 7 | 3 | 6 | … | 8 | 9 |
| … | … | … | … | … | |
| Объект m | $x_{1m}$ | $x_{2m}$ | … | $x_{nm}$ | $y_m$ |
Задачи множественной регрессии уже очень сложно представить на графике, ведь количество параметров каждого объекта обучающей выборки соответствует измерению, в котором находятся точки данных. Плюс нужно еще одно измерение для целевой переменной. И вместо того, чтобы подбирать оптимальную прямую, мы будем подбирать оптимальную гиперплоскость. Но в целом идея линейной регрессии остается неизменной.
Для удобства примем, что $ x_0^{(i)} = 1 $ для всех $i$. Другими словами, мы ведем некий суррогатный признак, для всех объектов равный единице. Это никак не сказывается на самой функции гипотезы, это лишь условность обозначения, но это сильно упростит математические выкладки, особенно в матричной форме.
| Признак 0 | Атрибут 1 | Атрибут 2 | … | Атрибут n | Целевая | |
|---|---|---|---|---|---|---|
| $x_0$ | $x_1$ | $x_2$ | … | $x_n$ | Y | |
| Объект 1 | 1 | 0 | 2 | … | 6 | 4 |
| Объект 2 | 1 | 1 | 4 | … | 3 | 7 |
| Объект 3 | 1 | 2 | 7 | … | 0 | 7 |
| Объект 4 | 1 | 3 | 2 | … | 3 | 8 |
| Объект 5 | 1 | 4 | 9 | … | 2 | 10 |
| Объект 6 | 1 | 5 | 7 | … | 15 | 9 |
| Объект 7 | 1 | 3 | 6 | … | 8 | 9 |
| … | … | … | … | … | … | |
| Объект m | 1 | $x_{1m}$ | $x_{2m}$ | … | $x_{nm}$ | $y_m$ |
Вообще, уравнения для алгоритмов машинного обучения, зависящие от нескольких параметров часто записываются в матричной форме. Это лишь способ сделать запись уравнений более компактной, а не какое-то новое знание. Если вы не владеете линейной алгеброй, то можете просто безболезненно пропустить эти формы записи уравнений. Однако, лучше, конечно, разобраться. Особенно это пригодится при изучении нейронных сетей.
Теперь определим множественную форму функции гипотезы следующим образом, используя несколько признаков. Она очень похожа на парную, но имеет больше входных переменных и, как следствие, больше параметров.
Общий вид модели множественной линейной регрессии:
\[h_b(x) = b_0 x_0 + b_1 x_1 + b_2 x_2 + ... + b_n x_n\]Или в матричной форме:
\[h\vec{y} = h_b(x) = X \cdot \vec{b}\]Используя определение матричного умножения, наша многопараметрическая функция гипотезы может быть кратко представлена в виде: $h(x) = B X$.
Обратите внимание, что в любой модели линейной регрессии количество параметров на единицу больше количества входных переменных. Это верно для любой линейной модели машинного обучения. Вообще, всегда чем больше признаков, тем больше параметров. Это будет важно для нас позже, когда мы будем говорить о сложности моделей.
Теперь, когда мы знаем виды функции гипотезы, то есть нашей модели, мы можем переходить к следующему шагу: функции ошибки. Мы построим ее по аналогии с функцией ошибки для парной модели. Для множественной регрессии функция ошибки от вектора параметров b выглядит следующим образом:
Функция ошибки для множественной линейной регрессии:
\[J(\vec{b}) = \frac{1}{2m} \sum_{i=1}^{m} (h_b(x_i) - y_i)^2\]Или в матричной форме:
Обратите внимание, что мы специально не раскрываем выражение \(h_b(x_i)\). Это нужно, чтобы подчеркнуть, что форма функции ошибки не зависит от функции гипотезы, она выражается через нее.
Теперь нам нужно взять производную этой функции ошибки. Здесь уже нужно знать производную самой функции гипотезы, так как:
Напомним общий вид функции модели множественной линейной регрессии:
В такой формулировке мы представляем частные производные функции ошибки (градиент) через частную производную функции гипотезы. Это так называемое моделенезависимое представление градиента. Ведь для этой формулы совершенно неважно, какой функцией будет наша гипотеза. Пока она является дифференцируемой, мы можем использовать градиент ее функции ошибки. Именно поэтому метод градиентного спуска работает с любыми аналитическими моделями, и нам не нужно каждый раз заново “переизобретать” математику градиентного спуска, адаптировать ее к каждой конкретной модели машинного обучения. Достаточно изучить этот метод один раз, в общей форме.
Метод градиентного спуска для множественной регрессии определяется следующими уравнениями:
повторять до сходимости:
\[b_0 := b_0 - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_b(x_i) - y_i)\] \[b_1 := b_1 - \alpha \frac{1}{m} \sum_{i=1}^{m} \Big( (h_b(x_i) - y_i) \cdot x_{1i} \Big)\] \[...\] \[b_j := b_j - \alpha \frac{1}{m} \sum_{i=1}^{m} \Big( (h_b(x_i) - y_i) \cdot x_{ji} \Big)\]Если же подставить $x_0 = 1$, то все уравнения представляются в очень однообразной форме, которую в общем виде можно записать так:
Или в матричной форме:
Выводы:
- Множественная регрессия очень похожа на парную, но с большим количеством признаков.
- Для удобства и однообразия, почти всегда обозначают $x_0 = 1$.
- Признаки образуют матрицу, поэтому уравнения множественной регрессии часто приводят в матричной форме, так короче.
- Алгоритм градиентного спуска для множественной регрессии точно такой же, как и для парной.
Нормализация признаков
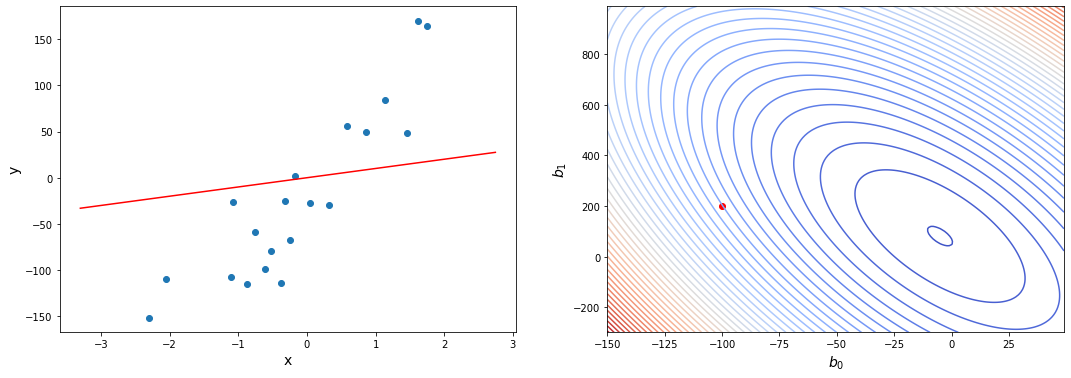
Мы можем ускорить сходимость метода градиентного спуска, преобразовав входные данные таким образом, чтобы все атрибуты имели значения примерно в том же диапазоне. Это называется нормализация данных - приведение всех признаков к одной шкале. Это ускоряет сходимость градиентного спуска за счет эффекта масштаба. Дело в том, что зачастую значения разных признаков измеряются по шкалам с очень разным порядком величины. Например, $x_1$ измеряется в миллионах, а $x_2$ - в долях единицы. Тогда “рабочий диапазон” параметров линейной регресси $b_j$ тоже получится очень разный по величине.
В таком случае форма функции ошибки будет очень вытянутой.
Вот как это может выглядеть в виде контурного графика:
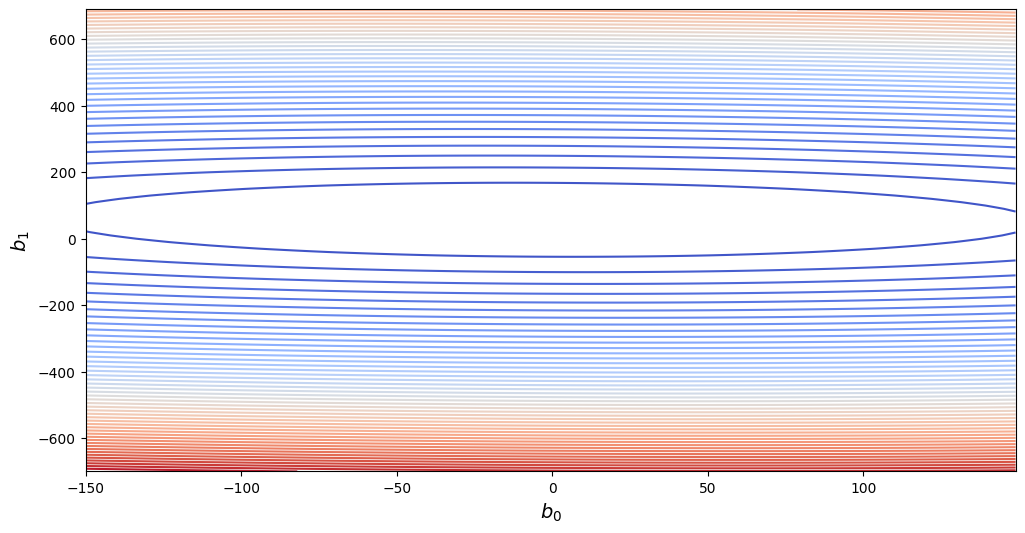
Это не проблема для математической формализации градиентного спуска - при достаточно малых $\alpha$ метод все равно рано или поздно сходится. Проблема в практической реализации. Получается, что если выбрать скорость обучения выше определенного предела по самому компактному признаку, спуск разойдется. Значит, скорость обучения надо делать меньше. Но тогда в направлении второго признака спуск будет проходить слишком медленно. И получается, что градиентный спуск потребует гораздо больше итераций для завершения.
Эту проблему можно решить если изменить диапазоны входных данных, чтобы они выражались величинами примерно одного порядка. Это не позволит одному измерению численно доминировать над другим. На практике применяют несколько алгоритмов нормализации, самые распространенные из которых - минимаксная нормализация и стандартизация или z-оценки.
Рассмотрим такой датасет для примера:
| Атрибут 1 | Атрибут 2 | Целевая | |
|---|---|---|---|
| $x_1$ | $x_2$ | Y | |
| Объект 1 | 0,5 | 200 | 4 |
| Объект 2 | 0,7 | 400 | 7 |
| Объект 3 | 1,0 | 300 | 7 |
| Объект 4 | 0,6 | 100 | 8 |
| Объект 5 | 0,8 | 500 | 10 |
Минимаксная нормализация - это изменение входных данных по следующей формуле:
После преобразования все значения будут лежать в диапазоне $x \in [0; 1]$.
Нормализация происходит независимо по каждому столбцу. Возьмем первый атрибут. Минимальное значение по нему - 0,5. Максимальное - 1,0. Подставляя в формулу каждое значение атрибута получаем:
| Атрибут 1 | Атрибут 2 | Целевая | |
|---|---|---|---|
| $x_1$ | $x_2$ | Y | |
| Объект 1 | 0,0 | 200 | 4 |
| Объект 2 | 0,4 | 400 | 7 |
| Объект 3 | 1,0 | 300 | 7 |
| Объект 4 | 0,2 | 100 | 8 |
| Объект 5 | 0,6 | 500 | 10 |
Теперь второй столбец:
| Атрибут 1 | Атрибут 2 | Целевая | |
|---|---|---|---|
| $x_1$ | $x_2$ | Y | |
| Объект 1 | 0,0 | 0,25 | 4 |
| Объект 2 | 0,4 | 0,75 | 7 |
| Объект 3 | 1,0 | 0,5 | 7 |
| Объект 4 | 0,2 | 0 | 8 |
| Объект 5 | 0,6 | 1 | 10 |
Z-оценки или стандартизация производится по формуле:
В таком случае данный признак приводится к стандартному распределению, то есть такому, у которого среднее 0, а дисперсия - 1.
У каждого из этих двух методов нормализации есть по два параметра. У минимаксной - минимальное и максимальное значение признака. У стандартизации - выборочные среднее и дисперсия. Параметры нормализации, конечно, вычисляются по каждому признаку (столбцу данных) отдельно. Причем, эти параметры надо запомнить, чтобы при использовании модели для предсказании использовать именно их (вычисленные по обучающей выборке). Даже если вы используете тестовую выборку, ее надо нормировать с использованием параметров, вычисленных по обучающей. Да, при этом может получиться, что при применении модели на данных, которых не было в обучающей выборке, могут получиться значения, например, меньше нуля или больше единицы (при использовании минимаксной нормализации). Это не страшно, главное, что будет соблюдена последовательность вычисления нормированных значений.
Про использование обучающей и тестовой выборок мы будем говорить значительно позже, при рассмотрении диагностики моделей машинного обучения.
Целевая переменная не нормируется. Это просто не нужно, а если ее нормировать, это сильно усложнит все математические расчеты и преобразования.
При использовании библиотечных моделей машинного обучения беспокоиться о нормализации входных данных вручную, как правило, не нужно. Большинство готовых реализаций моделей уже включают нормализацию как неотъемлемый этап подготовки данных. Более того, некоторые типы моделей обучения с учителем вовсе не нуждаются в нормализации. Но об этом пойдет речь в следующих главах.
Выводы:
- Нормализация нужна для ускорения метода градиентного спуска.
- Есть два основных метода нормализации - минимаксная и стандартизация.
- Параметры нормализации высчитываются по обучающей выборке.
- Нормализация встроена в большинство библиотечных методов.
- Некоторые методы более чувствительны к нормализации, чем другие.
- Нормализацию лучше сделать, чем не делать.
Практическое построение регрессии
В данной главе мы посмотрим, как можно реализовать методы линейной регрессии на практике. Сначала мы попробуем создать алгоритм регрессии с нуля, а затем воспользуемся библиотечной функцией. Это поможет нам более полно понять, как работают модели машинного обучения в целом и в библиотеке sckikit-learn (самом популярном инструменте для создания и обучения моделей на языке программирования Python) в частности.
Для понимания данной главы предполагаем, что читатель знаком с основами языка программирования Python. Нам понадобится знание его базового синтаксиса, немного - объектно-ориентированного программирования, немного - использования стандартных библиотек и модулей. Никаких продвинутых возможностей языка (типа метапрограммирования или декораторов) мы использовать не будем.
Как должны быть представлены данные для машинного обучения?
Применение любых моделей машинного обучения начинается с подготовки данных в необходимом формате. Для этого очень удобными для нас будут библиотеки numpy и pandas. Они практически всегда используются совместно с библиотекой sckikit-learn и другими инструментами машинного обучения. В первую очередь мы будем использовать numpy для создания массивов и операций с векторами и матрицами. Pandas нам понадобится для работы с табличными структурами - датасетами.
Если вы хотите самостоятельно задать в явном виде данные обучающей выборки, то нет ничего лучше использования обычных массивов ndarray. Обычно в одном массиве хранятся значения атрибутов - x, а в другом - значения целевой переменной - y.
1
2
3
4
5
6
7
8
9
10
11
import numpy as np
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
Если мы имеем дело с задачей множественной регрессии, то в массиве атрибутов будет уже двумерный массив, состоящий из нескольких векторов атрибутов, вот так:
1
2
3
4
5
x = np.array([
[0, 1, 2, 3, 4],
[5, 4, 9, 6, 3],
[7.8, -0.1, 0.0, -2.14, 10.7],
])
Важно следить за тем, чтобы в массиве атрибутов в каждом вложенном массиве количество элементов было одинаковым и в свою очередь совпадало с количеством элементов в массиве целевой переменной. Это называется соблюдение размерности задачи. Если размерность не соблюдается, то модели машинного обучения будут работать неправильно. А библиотечные функции чаще всего будут выдавать ошибку, связанную с формой массива (shape).
Но чаще всего вы не будете задавать исходные данные явно. Практически всегда их приходится читать из каких-либо входных файлов. Удобнее всего это сделать при помощи библиотеки pandas вот так:
1
2
3
4
import pandas as pd
x = pd.read_csv('x.csv', index_col=0)
y = pd.read_csv('y.csv', index_col=0)
Или, если данные лежат в одном файле в общей таблице (что происходит чаще всего), тогда его читают в один датафрейм, а затем выделяют целевую переменную, и факторные переменные:
1
2
3
4
5
6
7
8
import pandas as pd
data = pd.read_csv('data.csv', index_col=0)
y = data.Y
y = data["Y"]
x = data.drop(["Y"])
Обратите внимание, что матрицу атрибутов проще всего сформировать, удалив из полной таблицы целевую переменную. Но, если вы хотите выбрать только конкретные столбцы, тогда можно использовать более явный вид, через перечисление выбранных колонок.
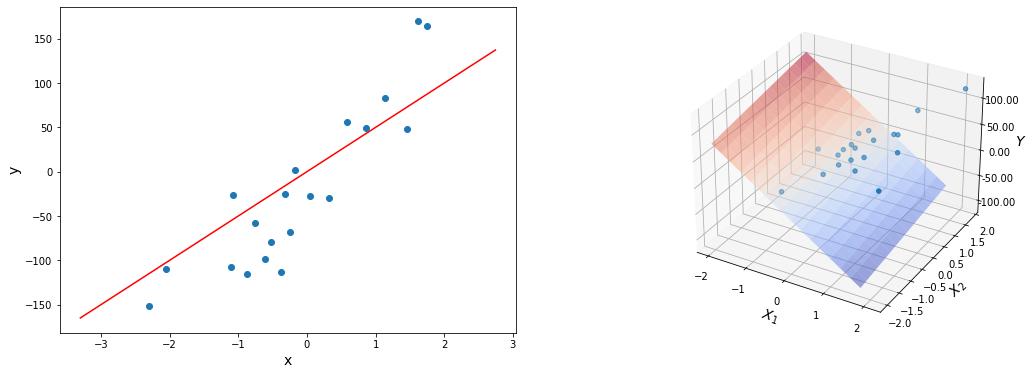
Если вы используете pandas или numpy для формирования массивов данных, то получившиеся переменные будут разных типов - DataFrame или ndarray, соответственно. Но на дальнейшую работу это не повлияет, так как интерфейс работы с этими структурами данных очень похож. Например, неважно, какие именно массивы мы используем, их можно изобразить на графике вот так:
1
2
3
4
5
import maiplotlib.pyplot as plt
plt.figure()
plt.scatter(x, y)
plt.show()
Конечно, такая визуализация будет работать только в случае задачи парной регрессии. Если x многомерно, то простой график использовать не получится.
Давайте соберем весь наш код вместе:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import pandas as pd
import maiplotlib.pyplot as plt
# x = pd.read_csv('x.csv', index_col=0)
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
# y = pd.read_csv('y.csv', index_col=0)
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
plt.figure()
plt.scatter(x, y)
plt.show()
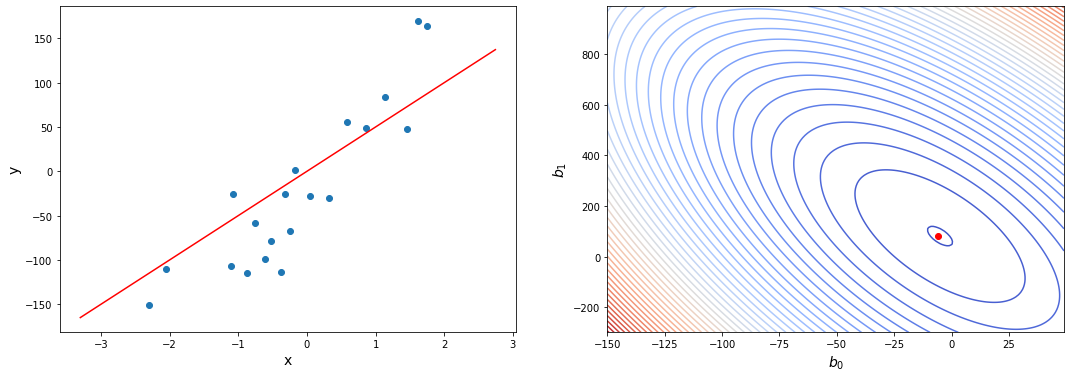
Это код генерирует вот такой вот график:
Как подбирать скорость обучения?
В нашей реализации метода градиентного спуска есть один параметр - скорость обучения - который нам приходится так же подбирать руками. Какой смысл автоматизировать подбор параметров линейной регрессии, если все равно приходится вручную подбирать какой-то другой параметр?
На самом деле подобрать скорость обучения гораздо легче. Нужно использовать тот факт, что при превышении определенного порогового значения ошибка начинает возрастать. Кроме того, мы знаем, что скорость обучения должна быть положительна, но меньше единицы. Вся проблема в этом пороговом значении, которое сильно зависит от размерности задачи. При одних данных хорошо работает $ \alpha = 0.5 $, а при каких-то приходится уменьшать ее на несколько порядков, например, $ \alpha = 0.00000001 $.
Мы еще не говорили о нормализации данных, которая тоже практически всегда применяется при обучении. Она “благотворно” влияет на возможный диапазон значений скорости обучения. При использовании нормализации меньше вероятность, что скорость обучения нужно будет уменьшать очень сильно.
Подбирать скорость обучения можно по следующему алгоритму. Сначала мы выбираем $ \alpha $ близкое к 1, скажем, $ \alpha = 0.7 $. Производим одну итерацию градиентного спуска и оцениваем, как изменилась ошибка. Если она уменьшилась, то ничего не надо менять, продолжаем спуск как обычно. Если же ошибка увеличилась, то скорость обучения нужно уменьшить. Например, раа в два. После чего мы повторяем первый шаг градиентного спуска. Таким образом мы не начинаем спуск, пока скорость обучения не снизится настолько, чтобы он начал сходиться.
Как применять регрессию с использованием scikit-learn?
Для серьезной работы, все-таки рекомендуется использовать готовые библиотечные решения. Они работаю гораздо быстрее, надежнее и гораздо проще, чем написанные самостоятельно. Мы будем использовать библиотеку scikit-learn для языка программирования Python как наш основной инструмент реализации простых моделей. Сегодня это одна их самых популярных библиотек для машинного обучения. Мы не будем повторять официальную документацию этой библиотеки, которая на редкость подробная и понятная. Наша задача - на примере этих инструментов понять, как работают и как применяются модели машинного обучения.
В библиотеке scikit-learn существует огромное количество моделей машинного обучения и других функций, которые могут понадобиться для их работы. Поэтому внутри самой библиотеки есть много разных пакетов. Все простые модели, например, модель линейной регрессии, собраны в пакете linear_models. Подключить его можно так:
1
from sklearn import linear_model
Надо помнить, что все модели машинного обучения из это библиотеки имеют одинаковый интерфейс. Это очень удобно и универсально. Но это значит, в частности, что все модели предполагают, что массив входных переменных - двумерный, а массивы целевых переменных - одномерный. Отдельного класса для парной регрессии не существует. Поэтому надо убедиться, что наш массив имеет нужную форму. Проще всего для преобразования формы массива использовать метод reshape, например, вот так:
1
x = x.reshape((-1, 1))
Если вы используете DataFrame, то они обычно всегда настроены правильно, поэтому этого шага может не потребоваться. Важно запомнить, что все методы библиотечных моделей машинного обучения предполагают, что в x будет двумерный массив или DataFrame, а в y, соответственно, одномерный массив или Series.
Эта строка преобразует любой массив в вектор-столбец. Это если у вас один признак, то есть парная регрессия. Если признаков несколько, то вместо 1 следует указать число признаков. -1 на первой позиции означает, что по нулевому измерению будет столько элементов, сколько останется в массиве.
Само использование модели машинного обучения в этой библиотеке очень просто и сводится к трем действиям: создание экземпляра модели, обучение модели методом fit(), получение предсказаний методом predict(). Это общее поведение для любых моделей библиотеки. Для модели парной линейной регрессии нам понадобится класс LinearRegression.
1
2
3
4
5
6
reg = linear_model.LinearRegression()
reg.fit(x, y)
y_pred = reg.predict(x)
print(reg.score(x, y))
print("Коэффициенты: \n", reg.coef_)
В этом классе кроме уже упомянутых методов fit() и predict(), которые есть в любой модели, есть большое количество методов и полей для получения дополнительной информации о моделях. Так, практически в каждой модели есть встроенный метод score(), который оценивает качество полученной модели. А поле coef_ содержит коэффициенты модели.
Обратите внимание, что в большинстве моделей коэффициентами считаются именно параметры при входящих переменных, то есть $ b_1, b_2, …, b_n $. Коэффициент $b_0$ считается особым и хранится отдельно в поле intercept_
Так как мы работаем с парной линейной регрессией, результат можно нарисовать на графике:
1
2
3
4
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
Как мы видим, результат ничем не отличается от модели, которую мы обучили сами, вручную:
Соберем код вместе и получим пример довольно реалистичного фрагмента работы с моделью машинного обучение. Примерно такой код можно встретить и в промышленных проектах по интеллектуальному анализу данных:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn.linear_model import LinearRegression
x = x.reshape((-1, 1))
reg = LinearRegression()
reg.fit(x, y)
print(reg.score(x, y))
from sklearn.metrics import mean_squared_error, r2_score
y_pred = reg.predict(x)
print("Коэффициенты: \n", reg.coef_)
print("Среднеквадратичная ошибка: %.2f" % mean_squared_error(y, y_pred))
print("Коэффициент детерминации: %.2f" % r2_score(y, y_pred))
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()