Задачи обучения без учителя
Машинное обучение без учителя (unsupervised learning, редко - неконтролируемое обучение) - это набор задач машинного обучения и анализа данных, при которых модель обучается выявлять внутренние паттерны и структуры в данных. При обучении без учителя в наборе данных (датасете) не выделяется явная целевая переменная.
Многие говорят, что обучение без учителя не преследует задачи получить конкретный результат. Но это не так, задачи обучения без учителя, так же как и задачи обучения с учителем - регрессия и классификация - четко сформулированы и имеют математическую формализацию.
Также некорректно говорить о том, что обучение делится на методы с учителем, если в датасете есть целевая переменная, и без учителя, если ее нет. Не вид датасета определяет тип моделей, которые мы можем применять, а те вопросы, на которые мы хотим получить ответы в процессе моделирования. Модели обучения с учителем исследуют связь значения определенной характеристики объектов обучающей выборки и значений других характеристик этих объектов. Таким образом они позволяют предсказать значение целевой переменной при известных значениях признаков.
Модели обучения без учителем отвечают на другие вопросы о данных. Конечно, так как они относятся к моделям машинного обучения, данные все равно обязательно должны быть, именно на них модель учится - то есть подбирает свои параметры. Но сама модель формализует внутреннюю структуру в этих данных. Конкретная цель моделирования в задачах обучения без учителя разная. Есть несколько типов задач обучения без учителя, и они отвечают на совершенно разные вопросы о данных.
Обычно среди задач обучения без учителя выделяют следующие типы: кластеризация (группировка схожих объектов обучающей выборки), понижение размерности (представление данных меньшим количеством признаков), обнаружение аномалий (определение объектов, по совокупности признаков не похожих на остальные объекты выборки), поиск ассоциаций (поиск взаимосвязей между существующими объектами).
В данном разделе мы познакомимся с классическими моделями обучения без учителя, их математической формализацией, метриками эффективности и реализацией на Python. Однако, довольно широко для решения всех этих задач применяются нейросетевые методы. Существуют специальные архитектуры нейронных сетей, методы обучения, которые позволяют сетям обучаться внутренней структуре данных. Так работают, например, карты Кохоннена. Но подробно это направление здесь мы рассматривать не будем.
Модели обучения без учителя довольно распространены на практике, так как могут дать ценную информацию об исследуемых объектах обучающей выборки, и, как следствие, на их примере, для всех объектов генеральной совокупности. Поэтому одна из главных характеристик моделей обучения без учителя (так же как и с учителем) - обобщающая способность. Как и во всем машинном обучении, мы стараемся на примере имеющегося у нас датасета получить выводы в виде обученной модели, которые можно обобщить и применять и для других объектов.
Поэтому при проведении обучения без учителя остаются справедливыми многие методологические аспекты, которые мы обсуждали в предыдущих разделах. В частности требуется собрать, очистить и представить определенным образом данные. Датасет также представляется в виде таблиц объект-признаки. То есть работает определение чистых данных. При этом обучающая выборка должна быть репрезентативна всей совокупности объектов, на которых впоследствии планируется использовать обученную модель. Иначе модель не будет иметь обобщающей способности. А для ее адекватного измерения также можно делить датасет на обучающую и тестовую выборки, измерять по ним разные метрики и диагностировать пере- и недообучение моделей.
Однако модели обучения без учителя могут применяться и не только самостоятельно. По своей сути, они прекрасно подходят для целей анализа и обработки данных. Например, обнаружение аномалий может применяться перед подготовкой данных для обучения моделей регрессии или классификации для удаления непоказательных объектов. Про возможности применения разных моделей обучения без учителя мы поговорим далее.
Выводы:
- Обучение без учителя - это набор задач выявления внутренней структуры в данных, при которых не выделяется целевая переменная.
- Модели обучения без учителя помогают ответить на иные вопросы, нежели обучение с учителем.
- Классические задачи обучения без учителя: кластеризациия, понижение размерности, обнаружение аномалий, поиск ассоциаций.
- Существует глубокое обучение без учителя.
- При обучении без учителя нужно следить за релевантностью обучающей выборки.
- При проведении обучения без учителя выборку также можно делить на обучающую и тестовую.
- Модели обучения без учителя используются для извлечения полезных сведений из данных.
- Модели обучения без учителя могут быть вспомогательными при предобработке данных для обучения с учителем.
Кластеризация
Довольно часто при анализе определенной выборки может быть полезно проанализировать, насколько схожие или различные объекты в ней представлены. Более того, можно задаться целью сгруппировать выборку по принципу схожести. То есть, разбить всю выборку на группы - непересекающиеся множества - таким образом, чтобы внутри каждой группы оказались максимально похожие друг на друга объекты.
Кластеризация - это задача обучения без учителя, которая заключается в нахождении оптимального разбиения выборки на некоторое количество непересекающихся множеств таким образом, чтобы схожие объекты (по совокупности значений всех признаков) оказались в одном кластере, а различные - в разных.
Математически задача кластеризации определяется так. У нас есть пространство признаков $\mathbb{X}$. Каждая точка обучающей выборки, то есть некоторый объект предметной области $x_i \in \mathbb{X}$. В общем случае, $\mathbb{X} = \mathbb{R}^m$, то есть если каждый признак выражен числом (а мы помним, что в процессе предобработки данных мы стремимся именно к такому представлению), то каждый объект - это точка в m-мерном пространстве, где m - количество признаков. Итого, обучающая выборка - это $X = {x_1, x_2, …, x_n} \subset \mathbb{X}$.
Итак, нам нужно сгруппировать эти объекты, то есть поставить в соответствие каждому объекту метку кластера (также как в задаче классификации мы ставим в соответствие объекту метку класса). На самом деле - не только каждой точке датасета, но даже каждой точке пространства признаков. Обученный алгоритм кластеризации может отнести к определенному кластеру и точку, которая ни разу не встречалась в обучающей выборке (опять же, как и модели классификации). Метки кластера обычно выбираются числами от 1 до $l$, где $l$ - это количество кластеров. Метка кластера обычно обозначается $y \in \mathbb{Y} = { 1, 2, …, l }$, по аналогии с задачей классификации. Поэтому функция кластеризации - это функция, которая переводит $\mathbb{X}$ в $\mathbb{Y}$.
Графически мы будем обозначать метку кластера также, как и метку класса в задачах обучения с учителем:
Но при такой визуализации следует помнить, что алгоритм кластеризации может отнести к тому или иному кластеру любую точку пространства признаков:
При этом количество кластеров обычно не известно заранее. Некоторым алгоритмам кластеризации (например, K-средних) нужно передать это количество как параметр, другие (DBSCAN) определяют его сами, исходя из других своих параметров (настроек). Но тем не менее, мы можем разбивать выборку на разное количество кластеров.
Для того, чтобы разбить выборку на кластеры нужно понимать, что именно мы понимаем под “похожестью” объектов. Для этого необходимо ввести меру близости объектов. Для кластеризации чаще используется метрика расстояния - некоторая функция, которая каждой паре точек пространства признаков ставит в соответствие неотрицательное число: расстояние между ними: $\rho(x, x’) \to [0; +\inf)$. Чаще всего используется мера Евклидова расстояния между точками: $\rho(x, x’) = \sum_{i=1}^{n} ( x_i - x_i ‘ )^2$. Эта мера расстояния достаточно неплохо работает на большинстве данных, выраженных в численной форме. Но при обучении на данных, имеющих специальную структуру, имеет смысл задуматься о выборе другой, более эффективной функции расстояния.
Кроме всего этого для полной формализации задачи кластеризации нам необходима и метрика качества. Также, как и в обучении с учителем, она ставит в соответствие каждой конкретной параметризации функции кластеризации число, которое показывает, насколько эта кластеризация “удачна”. Но в отличие от задач с учителем, мы не можем просто сверить ответы модели с правильными. В задачах обучения без учителя у нас нет никаких правильных ответов. Поэтому при оценивании качества модели мы должны посмотреть, как она работает на обучающей выборке, и сделать вывод о ее качестве только на основе внутренней структуры обучающей выборки. Поэтому, метрика качества кластеризации должна использовать саму обучающую выборку, матрицу признаков: $q(a, X) \to [0; +\inf)$. Этим она отличается от метрика качества в задачах обучения с учителем.
Например, одна из самых распространенных метрик, WCSS, рассчитывает так называемое внутрикластерное расстояние, то есть расстояния между всеми точками, которые модель отнесла к одному классу. Чем меньше это расстояние, тем компактнее получились кластеры. Значит, при прочих равных, модель нашла лучшее решение. Почему “при прочих равных”? Дело в том, что чем больше кластеров мы задаем, тем меньше будет это расстояние только за счет уменьшения их размеров. Поэтому метрика WCSS подвержена “инфляции”, она естественно снижается при увеличении количества кластеров. Некоторые метрики подвержены такой инфляции, другие - нет. Более подробно мы поговорим о метриках далее.
Кроме самой модели и обучающей выборки, метрика качества кластеризации еще, неявно, но обязательно должна опираться и еще на метрику расстояния. Технически, мы можем использовать разные метрики расстояния для обучения модели кластеризации и для оценки ее эффективности. Поэтому полное определение функционала (метрики) качества кластеризации выглядит так: $q(a, X, \rho) \to [0; +\inf)$.
Определив все эти составляющие, можно полностью специфицировать задачу кластеризации. В такой постановке она выглядит так: необходимо найти набор параметров конкретной модели кластеризации $a$, которая дает самую оптимальную кластеризацию обучающей выборки $X$ по метрике качества $q$: $a = argmax q(a, X)$. Поэтому вот полное формальное математическое определение задачи кластеризации:
$n$ - количество объектов в обучающей выборке;
$m$ - количество признаков каждого объекта;
$X = {x_1, x_2, …, x_n} \subset \mathbb{X}$ - обучающая выборка;
$a(x_i): \mathbb{X} \to \mathbb{Y} = {1, 2, …, l}$ - функция кластеризации;
$\rho(x_i, x_j): \mathbb{X} \times \mathbb{X} \to [0; +\inf)$ - функция расстояния между объектами;
$q(a, X, \rho) \to [0; +\inf)$ - метрика качества кластеризации;
$a = argmax q(a, X)$ - задача кластеризации;
Далее мы поговорим про разные классы моделей машинного обучения для решения задач кластеризации. Но самое главное определение во всем этом формализме - это, без сомнения, метрика качества. Именно она выражает формальным языком то, что конкретно мы понимаем под разбиением точек на группы. Казалось бы, при определении метрики расстояния между точками задача однозначна, но это совсем не так.
Более того, задача кластеризации принципиально не имеет единственно верного решения. Здесь есть три разных соображения. Во-первых, существует неоднозначность в определении целевого количества кластеров. В некоторых случаях, количество кластеров может определяться бизнес-требованиями, но чаще всего, оно следует из внутренней структуры данных. В некоторых случаях, потенциальное количество кластеров очевидно:
В этой выборке отчетливо прослеживается два кластера. Можно ли ее разбить на три или четыре? Технически, да. Однако, в таком случае, добавление нового кластера не даст существенного улучшения метрик. Ведь кластеры будут выглядеть искусственно, и не компактно.
С другой стороны, в других случаях, даже при взгляде на выборку нельзя однозначно определить сколько групп можно выделить. Вот классическое распределение:
На сколько групп можно разделить эту выборку: на два, три или четыре? Можно привести аргументы в пользу любого количества кластеров. Здесь нужно исходить из каких-то других соображений. Еще помните, что в реальных задачах, когда признаков больше двух, мы не сможем так просто изобразить всю обучающую выборку. И реальное распределение будет совершенно неочевидно. Поэтому нам придется ориентироваться исключительно на численные метрики.
Во-вторых, даже при жестко определенном количестве кластеров может возникнуть неоднозначность в определении группировки точек в эти кластеры. Давайте проанализируем выборку:
Казалось бы, здесь все очевидно. Четко прослеживаются четыре кластера. А что делать, если нам необходимо (по каким-то внешним соображениям) выделить только два? Конечно, нам нужно объединить самые близкие кластеры. Но функция расстояния у нас очень сильно зависит от масштаба данных. Если мы масштабируем выборку вдоль той или оной оси, у нас получится разная картина:
При этом, конечно, данные перед кластеризации желательно нормализовывать. Но такая ситуация все равно может возникнуть из-за разных диапазонов данных по разным признакам (осям). Форма распределения может оказывать влияние на результат кластеризации.
В-третьих, мы говорим о функции расстояния между двумя отдельными точками пространства признаков. Но в некоторых алгоритмах классификации приходится говорить о расстоянии точку с группой (кластером) или вообще о расстоянии между двумя кластерами точек. Здесь существует еще одна неоднозначность: считать расстояние между кластерами по самым ближайшим точкам, по самым дальним, по среднему расстоянию? Мы еще упомянем эти алгоритмы в одной из следующих глав.
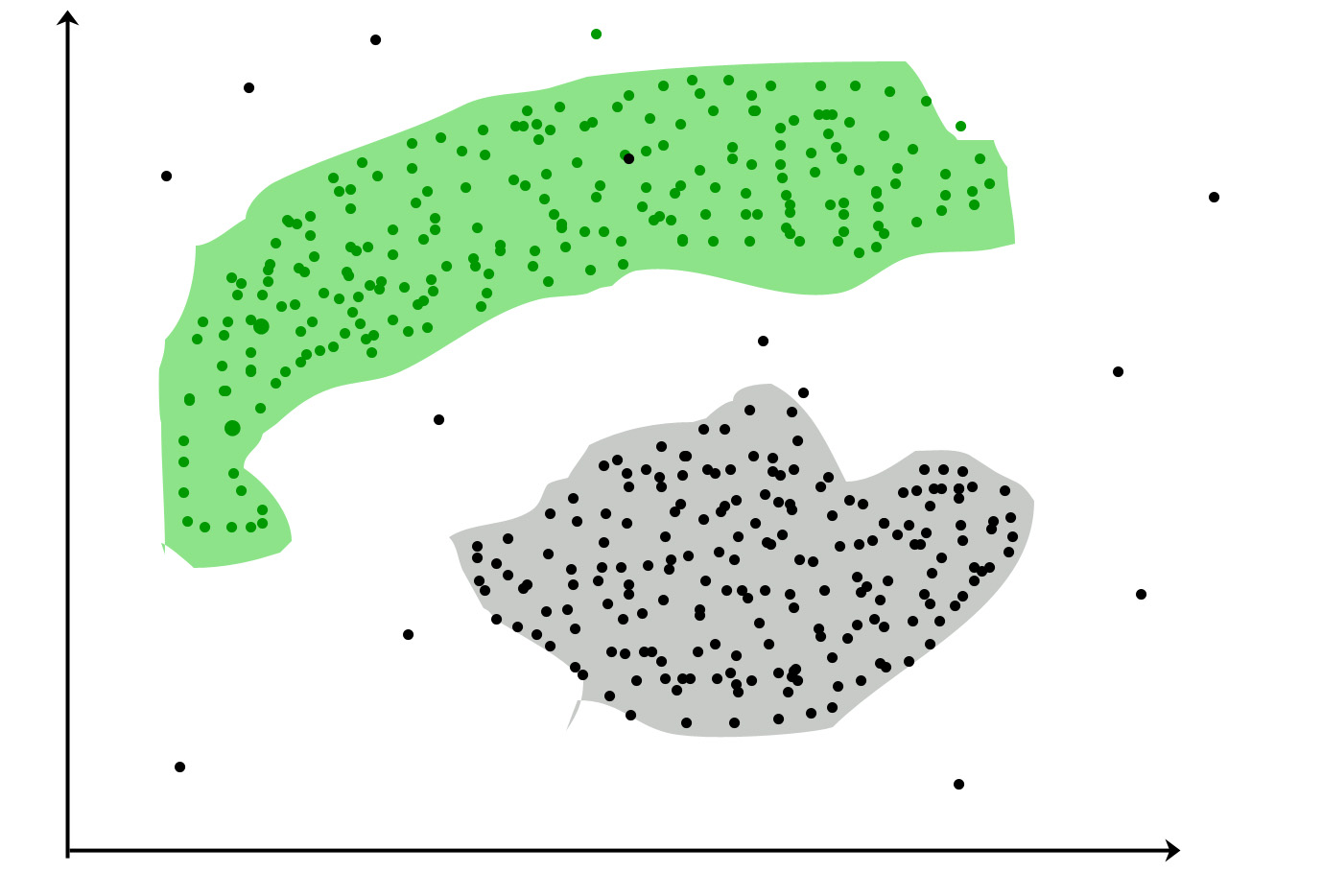
Еще одна трудность, про которую мы не будем говорить более подробно, это тот факт, что объекты предметной области могут группироваться вообще не по признаку близости. Посмотрите на следующее распределение:
Здесь методы кластеризации принципиально ничего не могут сделать, так как они по определению основаны на оценке близости. В таких случаях следует собирать больше данных, преобразовывать признаки таким образом, чтобы разные по природе группы объектов можно было бы дифференцировать по сходству.
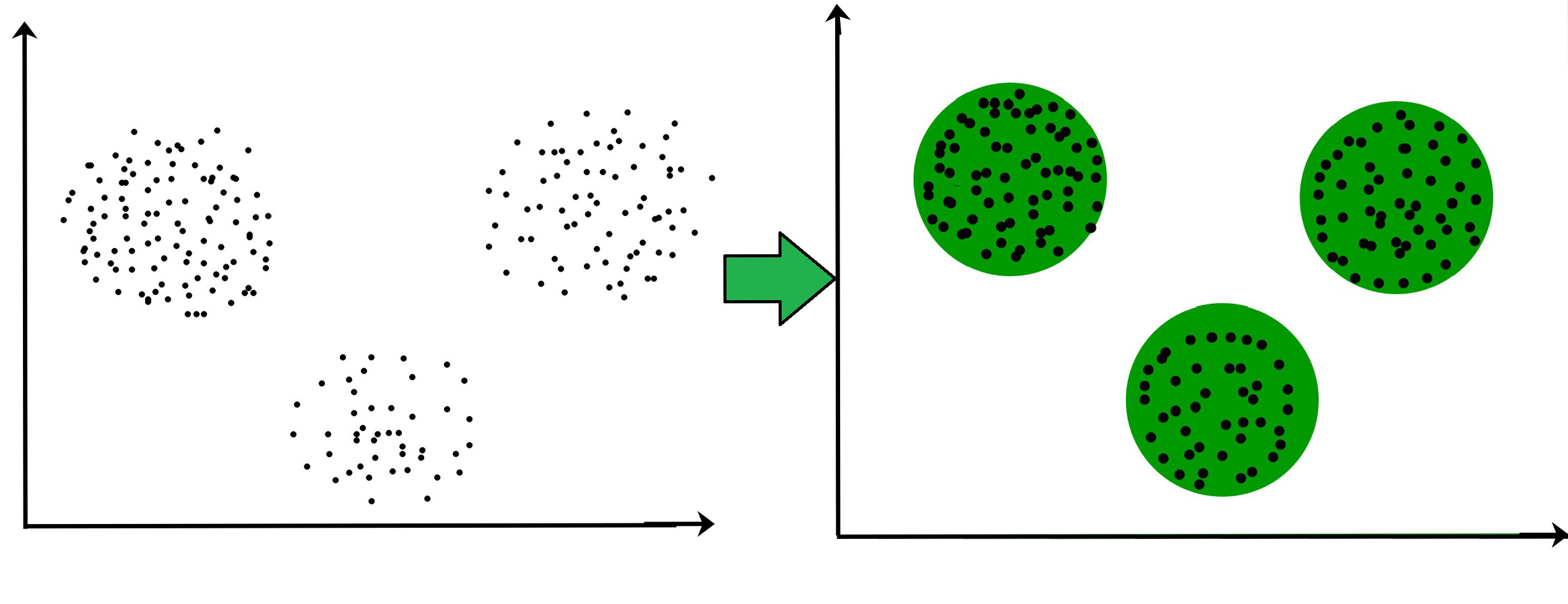
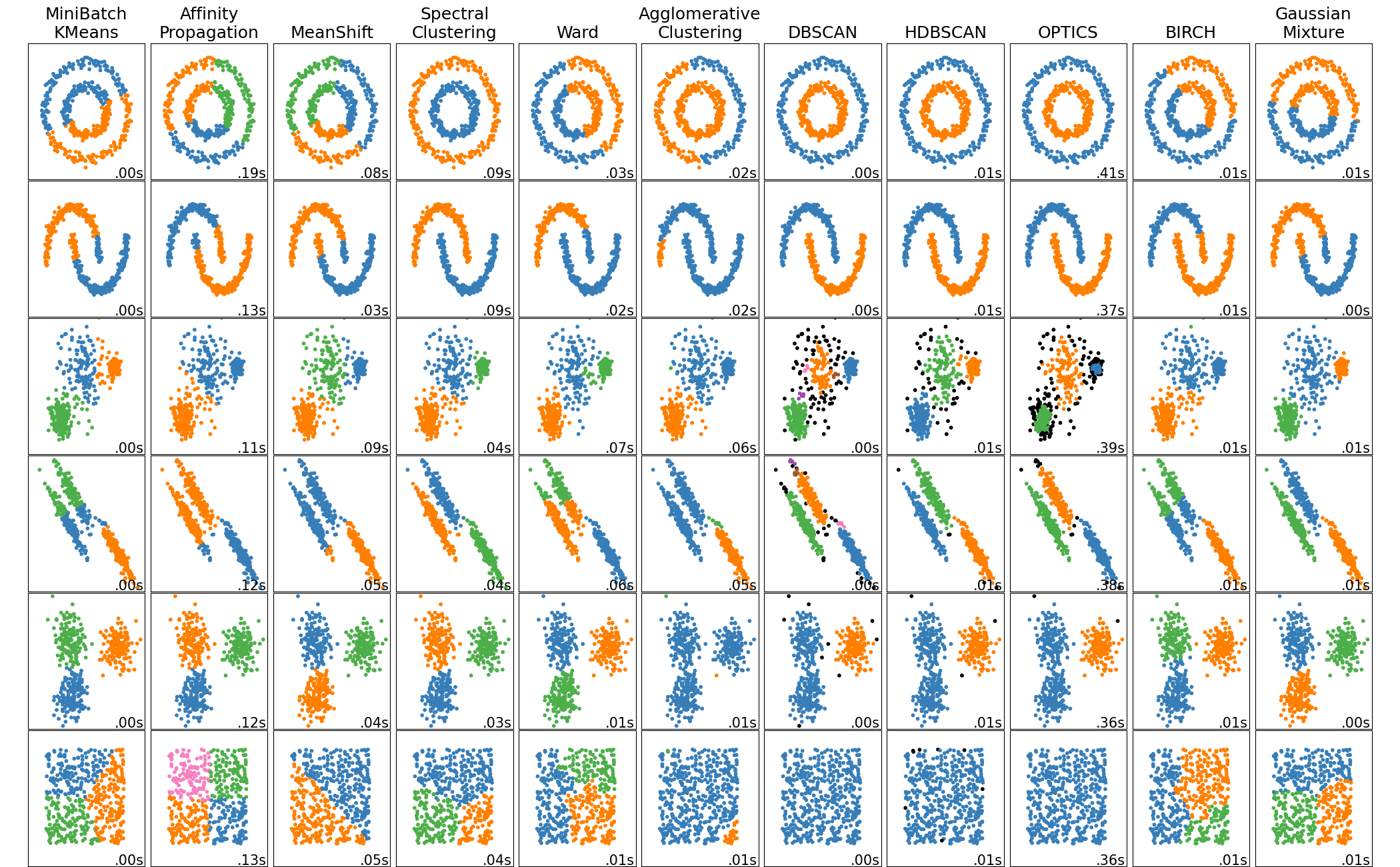
Существует множество разных моделей кластеризации. В зависимости от конкретного алгоритма, могут получаться кластеры произвольной формы. Также помним, что обычно мы моделируем в пространстве очень высоких размерностей. Все графики для наглядности изображаются на плоскости. Поэтому в общем виде мы не можем визуализировать кластеры и приходится ориентироваться на метрики.
Задачу кластеризации часто сравнивают с классификацией, но их нельзя путать. В задаче классификации мы знаем заранее, какие группы объектов у нас есть, сколько их и какой предметный смысл они несут. Это - целевая переменная в обучающей выборке. В случае с кластеризацией - ничего этого мы не знаем, задача именно в нахождении внутренней структуры в данных:
Именно поэтому модель сама может находить произвольные группы точек обучающей выборки. Как мы уже говорили, после кластеризации модель выдает принадлежность объектов кластерам. Сами кластеры не имеют никакого общего смысла. Эту результирующую группировку необходимо анализировать вручную и интерпретировать кластеры судя по тому, какие объекты в них находятся. При этом некоторые алгоритмы могут дополнительно выделять “шум” - объекты, которые не отнесены ни к одному кластеру.

Выводы:
- Кластеризация - разбиение объектов на непересекающиеся кластеры по схожести.
- Кластеров может получиться различное количество, в некоторых моделях можно задать его заранее.
- Сами кластеры не имеют предметного смысла, его надо искать вручную.
- Предпочтительно кластеры должны быть однородными.
- Кластеризация применяется при сегментации клиентов по параметрам.
- На вход может подаваться матрица признаков объектов, либо матрица расстояний между объектами, либо матрица сходства.
- Метрики расстояния или сходства могут применяться разные в зависимости от задачи.
- Кластеризация может применяться для сжатия данных - можно оставить по одному типичному представителю от каждого кластера.
- Решение задачи кластеризации принципиально неоднозначно.
Метрики качества кластеризации
Метод K-средних
Метод К-средних (K means) - это один из самых популярных алгоритмов кластеризации. По аналогии с методом k ближайших соседей он основан на идее вычисления расстояний между точками выборки. Алгоритм строится на приципе минимизации внутрикластерного расстояния, то есть метрики WCSS (within-cluster sum of squares):
где k - число кластеров, $S_i$ - сами кластеры, $\mu_i$ - центр i-го кластера.
Для начала работы алгоритма необходимо задать необходимое количество кластеров. Затем в пространстве признаков выбираются случайные центры этих кластеров. Центры желательно выбирать так, чтобы к каждому кластеру принадлежала хотя бы одна точка. Есть несколько алгоритмов выбора
Затем алгоритм итеративно повторяет два шага:
- Случайный выбор центров
- Итеративно до сходимости:
- Распределение
- Обновление
На этапе распределения каждая точка относится к тому кластеру, центр которого к ней ближе. На этапе обновления центр каждого кластера заменяется на центр масс всех принадлежащих точек.
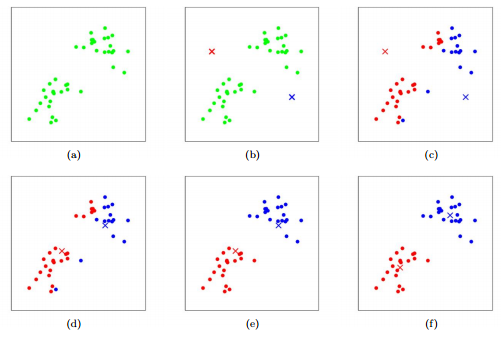
Рано или поздно на этапе обновления центры кластеров сместятся так, что ни одна точка не поменяет своего распределения. Это означает схождение алгоритма и завершение цикла. Итоговые центры кластеров и определяют результат кластеризации.

Алгоритм сходится всегда. Правда, иногда алгоритм “сваливается” в локальный оптимум:
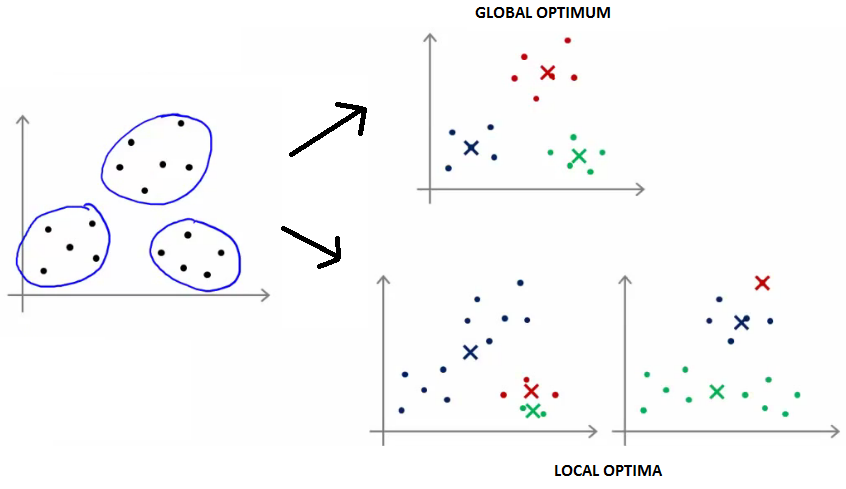
Алгоритм имеет экспоненциальную сложность по количеству признаков. Поэтому в очень высокомерных пространствах он может быть неэффективен.
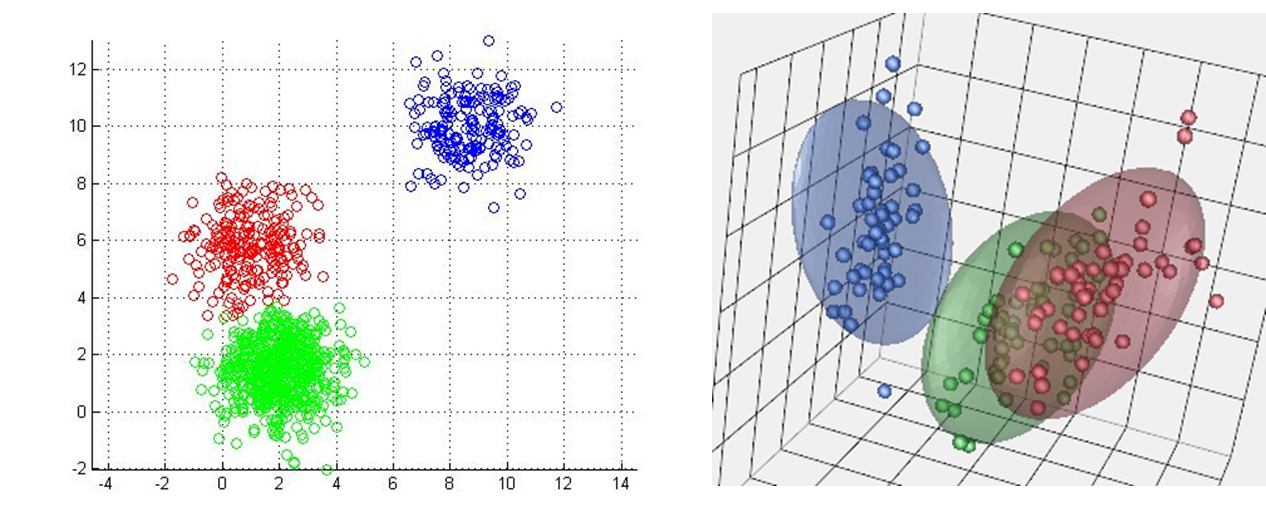
Большим недостатком метода является то, что для его инициализации нужно задать количество кластеров. Обычно оно не известно заранее. Для выбора лучшего количества применяют “метод локтя”. Для этого нужно построить кластеризацию с разным количеством кластеров и построить график зависимости метрики WCSS от количества кластеров. Чем больше количество, тем более равномерными они получатся. Поэтому мы увидим примерно такую картину:

Метод локтя заключается а том, что мы выбираем такое количество кластеров, которое сильно снижает метрику WCSS, а при большем количестве она снижается уже не так сильно. То есть мы ищем “локоть” на этом графике. В данном примере адекватное количество кластов - 2 или 3.
1
2
3
4
5
6
7
8
9
10
11
from sklearn import datasets
from sklearn.cluster import KMeans
iris_df = datasets.load_iris()
model = KMeans(n_clusters=3)
model.fit(iris_df.data)
predicted_label = model.predict([[7.2, 3.5, 0.8, 1.6]])
all_predictions = model.predict(iris_df.data)
Выводы:
- К-средних - это один из самых простых и распространенных алгоритмов кластеризации.
- Необходимо задание количества кластеров.
- Есть несколько алгоритмов выбора начальных центров кластеров. Обычно берут случайные точки выборки.
- Итеративный алгоритм с гарантированной сходимостью и простым критерием.
- Алгоритм не гарантирует нахождение глобального оптимума. Может сойтись к локальному.
- Для выбора оптимального количества кластеров применяют метод локтя.
- Эффективен, когда формы кластеров близки к гиперсферическим.
Иерархическая кластеризация
Иерархическая кластеризация - это набор алгоритмов, которые не только распределяют объекты по кластерам, но и определяют взаимные расстояния между самими кластерами. Таким образом можно объединять небольшие кластеры в группы, или разделять большие кластеры на подкластеры. Таким образом формируется иерархия кластеров.
Агломеративная иерархическая кластеризация - это алгоритм последовательного объединения объектов в кластеры по мере близости. Изначально каждый объект представляется в виде отдельного кластера. Затем итеративно самые близкие кластеры объединяются пока не останется один, влючающий все объекты выборки. Последовательноть этого объединения и задает иерархию кластеров.
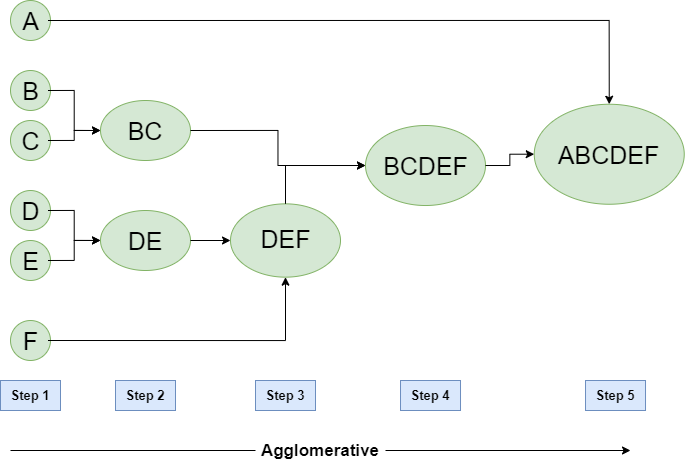
Разделяющая кластеризация менее распространена. При таком алгоритме наоборот, происходит последовательное разделение кластеров так, чтобы минимизировать метрику WCSS или другую выбранную.
1
2
3
4
5
6
7
8
9
from sklearn.cluster import AgglomerativeClustering
import numpy as np
X = np.array([[1, 2], [1, 4], [1, 0],
[4, 2], [4, 4], [4, 0]])
clustering = AgglomerativeClustering(n_clusters=2).fit(X)
print(clustering.labels_)
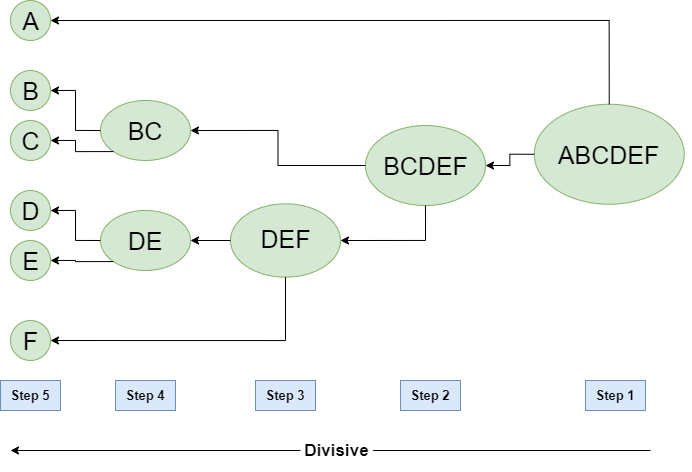
При объединении двух кластеров необходимо проверять расстояние между ними в каждой паре кластеров и объединяем пару с наименьшим расстоянием/наибольшим сходством. Но вопрос в том, как определяется это расстояние. Существуют различные способы определения расстояния/сходства между кластерами. Самые распространенные:
- Минимальное расстояние.
- Максимальное расстояние.
- Среднее значение по группе.
- Метод Уорда.
Метод Уорда: Сходство двух кластеров основано на увеличении WCSS при объединении двух кластеров.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
import pandas as pd
seeds_df = pd.read_csv("http://qps.ru/jNZUT")
varieties = list(seeds_df.pop('grain_variety'))
samples = seeds_df.values
mergings = linkage(samples, method='complete')
dendrogram(mergings,
labels=varieties,
leaf_rotation=90,
leaf_font_size=6,
)
plt.show()
Результаты иерархической кластеризации чаще всего представляют на дендрограмме. По горизонтали в самом низу графика располагаются объекты выборки. Объединение кластеров показано линиями на графике. Причем по вертикали отложено значение метрики, например, WCSS.
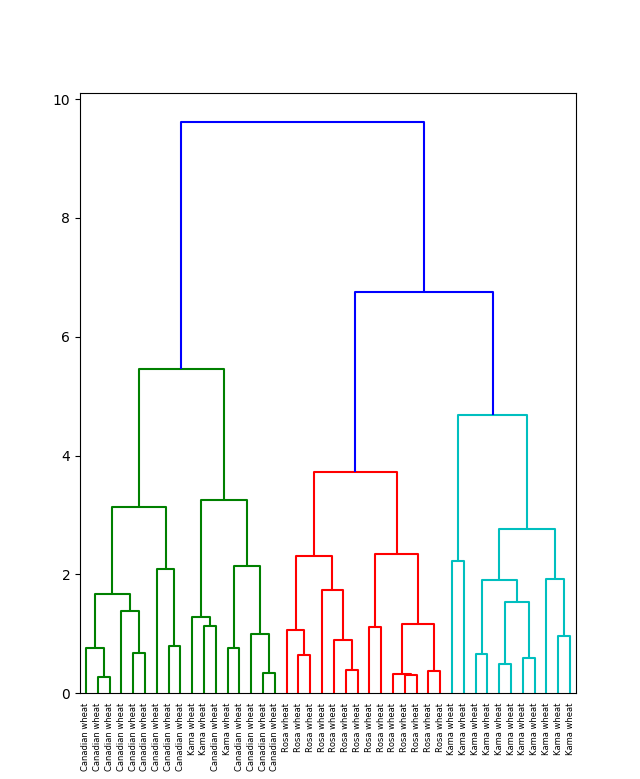
Таким образом по дендрограмме можно определить относительную близость объектов. А выбрав определенный уровень метрики, то есть уровень на вертикальной шкале, можно определить нужные по задаче кластеры.
Выводы:
- Иерархическая кластеризация удобна для определения близости объектов. Либо когда уже задана матрица близости.
- Для иерархической кластеризации не нужно задавать определенное количество кластеров.
- После иерархической кластеризации можно выделить какое угодно количество кластеров, в зависимости от потребности задачи.
- Можно определить целевой уровень близости объектов и найти соотвестствующие ему кластеры.
- Иерархическая кластеризация довольно плохо масштабируется по количеству объектов. Стоит применять при небольшом объеме выборки.
- Результаты кластеризации можно визуализировать на дендрограмме.
- В отличие от метода K-средних, дает воспроизводимый результат.
DBSCAN
DBSCAN (Density-Based Spatial Clustering of Applications with Noise, плотностный алгоритм пространственной кластеризации с присутствием шума) – популярный алгоритм кластеризации, используемый в анализе данных в качестве одной из замен метода k-средних.
Методы, основанные на разделении точек (K-средние, PAM-кластеризация) и иерархические методы кластеризации позволяют находить кластеры близкой к сферической формы и выпуклые кластеры. Другими словами, они подходят только для компактных и хорошо разделенных кластеров. Кроме того, на них также серьезно влияет наличие шума и выбросов в данных.
Реальные данные могут содержать проблемы, которые существенно осложняют применение таких классических методво кластеризации:
- Кластеры могут быть произвольной формы
- Кластеры могут быть вложенными
- Данные могут содержать шум
- Кластеры могут не быть линейно разделимыми
Алгоритм DBSCAN решает эти проблемы тем, что оперирует понятиями плотности, связности и достижимости точек. На концептуальном уровне он ближе к интуитивному пониманию понятия “кластер” человеком.
Для работы алгоритма DBSCAN необходимо выбрать значение двух параметров - радиус окрестности точки $\epsilon$ и минимальное количество точек в этом радиусе $m$. Основа алгоритма DBSCAN в том, что все точки выборки делятся на три категории.
Основные (центральыне) точки - это такие точки выборки, в окрестностях которых (радиусом, который задан перед началом работы алгоритма $\epsilon$) находятся не менее заданного количества точек $m$. Например на картинке ниже минимальное количество точек задано равным 4, а радиус окрестности показан окружностями:
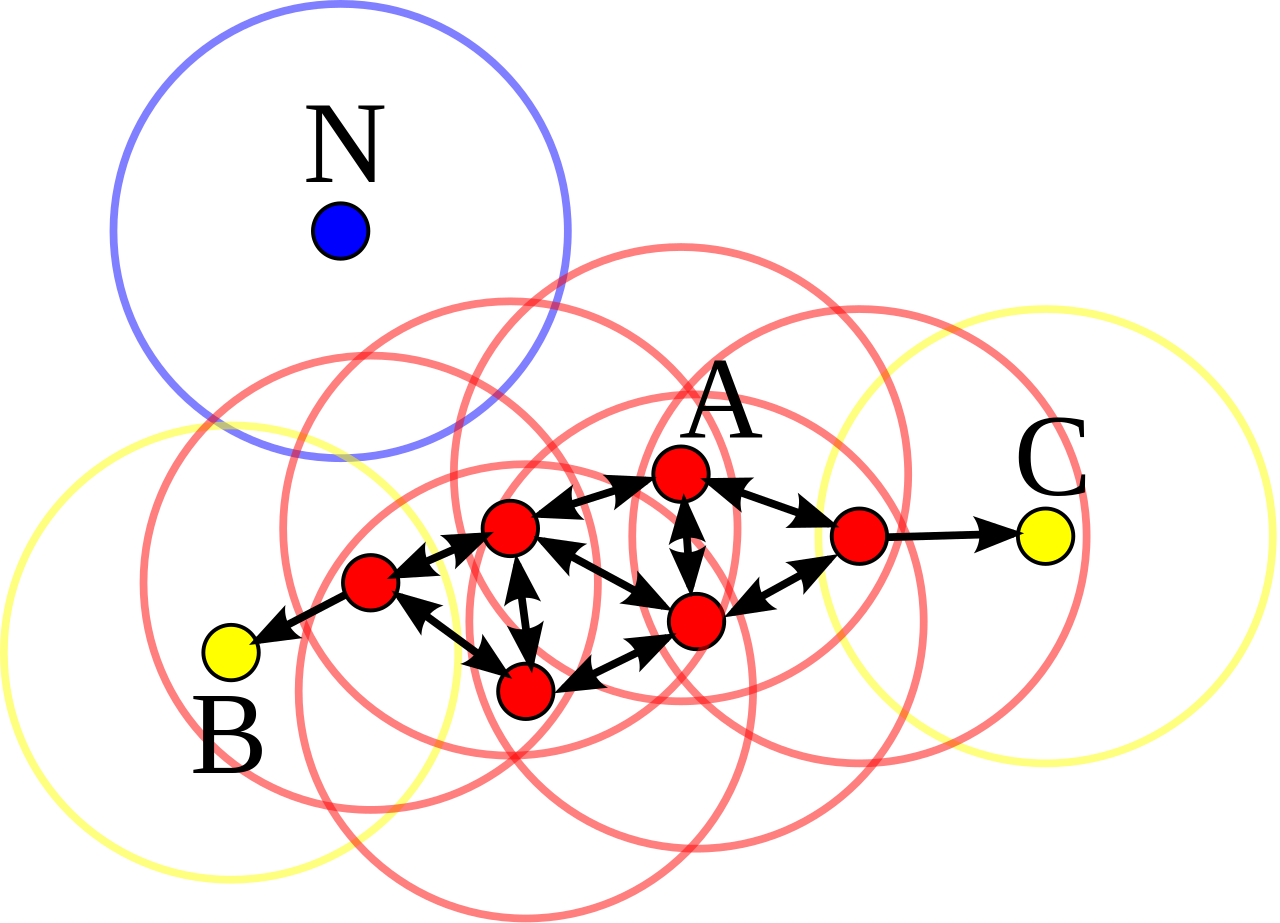
Неосновная точка - это такая, в окрестностях которой меньше заданного количества точек $m$, но есть хотя бы одна основная. А точка шума - это та, в окрестностях которой мало точек, и нет ни одной основной.
Все основные точки на первом этапе алгоритма счтаются отдельными кластерами. После определения основной точки нужно обойти всех соседей этой точки (еще говорят, точки, достижимые из заданной). Все они будут относиться к тому же кластеру, что и изначальная.
Алгоритм повторяется с разными точками выборки пока все они не станут классифицированы. После этого будут сформированы все кластеры и точки шума, не относимые ни к одному кластеру. При этом все кластеры получаются внутренне связанные.

Применение алгоритма в библиотеке sklearn ничем не отличается от других моделей кластеризации:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
X, y_true = make_blobs(n_samples=300, centers=4,
cluster_std=0.50, random_state=0)
db = sklearn.cluster.DBSCAN(eps=0.3, min_samples=10).fit(X)
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
for k, col in zip(set(labels), ['y', 'b', 'g', 'r']):
if k == -1:
col = 'k'
class_member_mask = (labels == k)
xy = X[class_member_mask & core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=col)
xy = X[class_member_mask & ~core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=col)
plt.title('number of clusters: %d' % n_clusters_)
Обратите внимание на работу с полями обученной модели. В этом листинге основной объем занимает работа с организацией визуализации построенных кластеров. Этот код генерирует такой результат:
.png)
В сравнении с методом К-средних особенно ярко проявляются специфические черты алгоритма DBSCAN относительно распозначания формы кластеров и работы с шумом:

Алгоритм довольно чувствителен к выбору изначальных параметров $m$ и $\epsilon$:
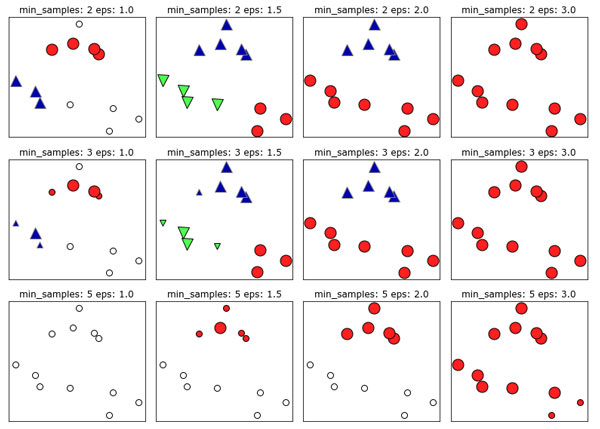
Существуют эвристики для выбора $m$ и $\epsilon$. Чаще всего применяется такой метод и его вариации:
- Выберите $m$. Обычно используются значения от 3 до 9, чем более неоднородный ожидается датасет, и чем больше уровень шума, тем большим следует взять $m$.
- Вычислите среднее расстояние по $m$ ближайшим соседям для каждой точки. Т.е. если $m=3$, нужно выбрать трёх ближайших соседей, сложить расстояния до них и поделить на три.
- Сортируем полученные значения по возрастанию и выводим на экран.
- Видим что-то вроде такого резко возрастающего графика. Следует взять $\epsilon$ где-нибудь в полосе, где происходит самый сильный перегиб. Чем больше $\epsilon$, тем больше получатся кластеры, и тем меньше их будет.
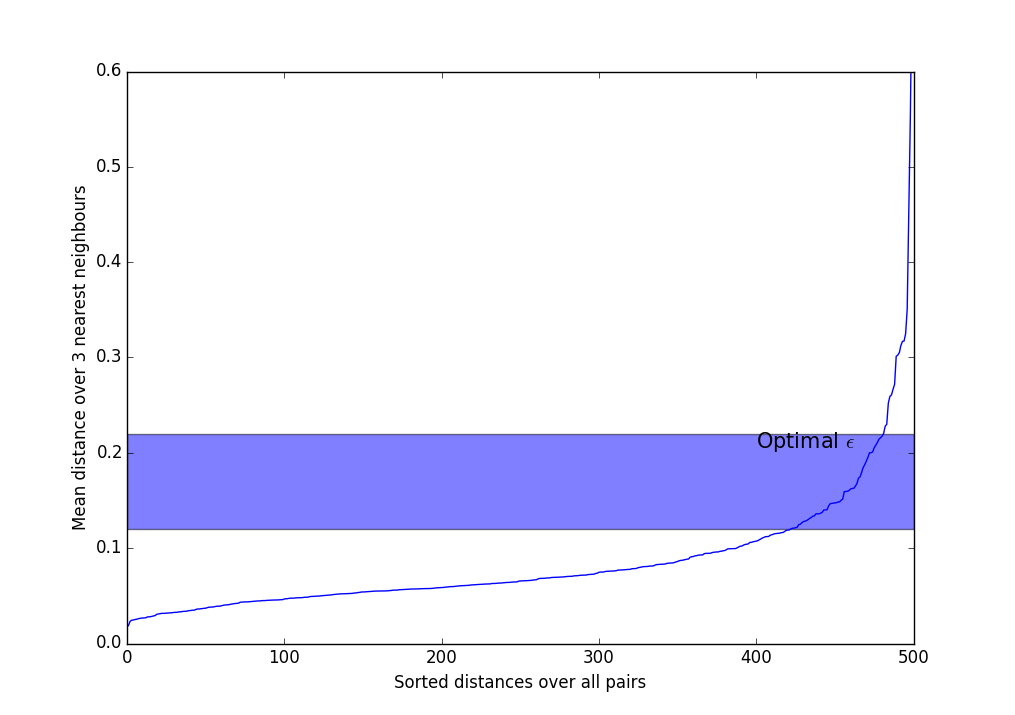
Выводы:
- Метод DBSCAN основан на анализе плотности распредления точек выборки.
- Метод может находить кластеры произвольной формы, в том числе, вложенные.
- Метод основан на предположении, что рядом с каждой точной кластера должно быть не менее определенного числа точек этого же кластера.
- Единственный метод кластеризации, который явно выделяет шум.
- Алгоритм не требует задания количества кластеров.
- DBSCAN плохо работает с кластерами очень разной плотности.
- Алгоритм не полностью однозначен, его результат зависит от порядка обхода точек.
- Чаще всего применяетя Евклидова метрика расстояния.
HDBSCAN
OPTICS
Метод нечетких C-средних
Понижение размерности
Задача понижения размерности определяется как нахождение оптимального представления некоторого данного множества точек пространства высокой размерности в пространстве более низкой размерности таким образом, чтобы сохранить как можно больше информации. Понижение размерности полезно применять в тех случаях, когда количество признаков в наборе данных представляет проблему.
Большое количество признаков может доставлять следующие сложности в процессе проведения анализа данных и машинного обучения:
- Сложность визуализации
- Вычислительная сложность
- Повышенные требования к памяти
- Склонность к переобучению
- Присутствие в данных шума
- Проклятие размерности
Совокупность этих факторов приводит к тому, что эффективность моделей машинного обучения может снижаться с ростом количества признаков:
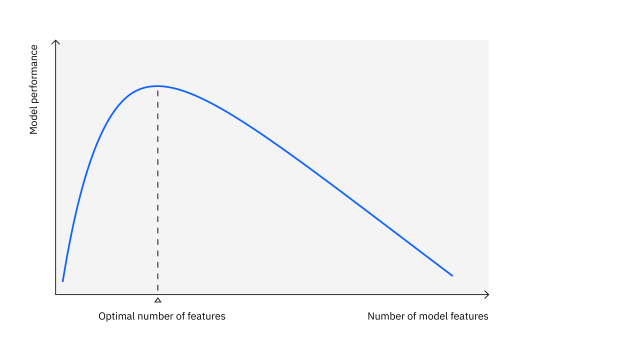
Понижение размерности стремится представить данные с меньшим количеством признаков. Во многом это работает как проекция исходного многообразия точек. Естественно, выбор проекции оказывает существенное влияние на результат:
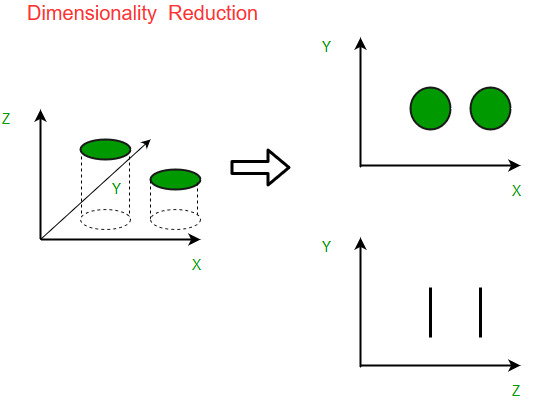
При этом для проекции можно выбирать не только оси исходного пространства, но и произвольные вектора:
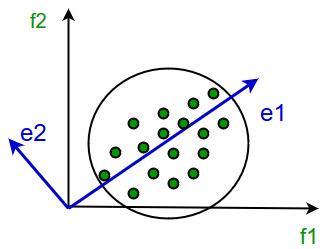
При этом некоторые проекции оказываются хуже или лучше других. Например, проекция, которая “перемешивает” точки исходного распределения не очень эффективна:
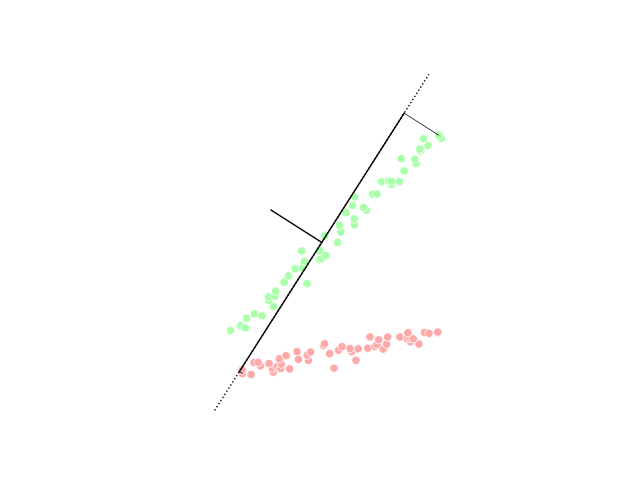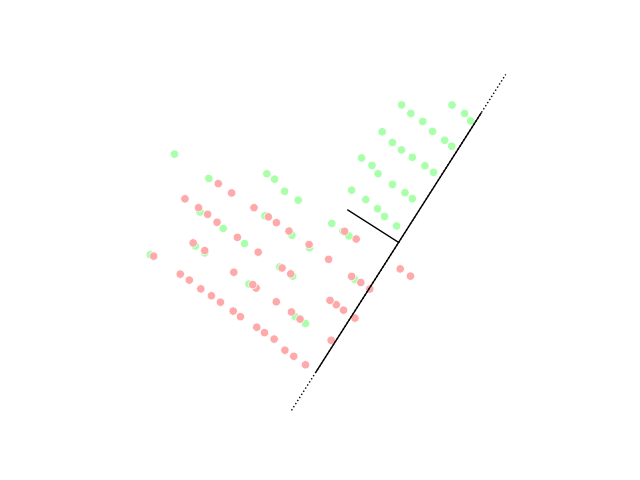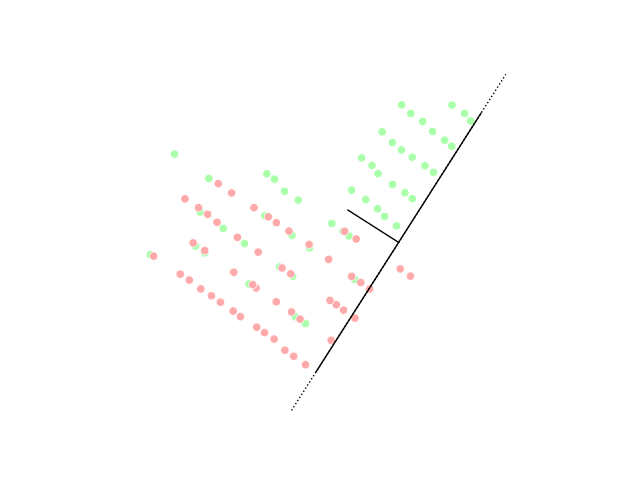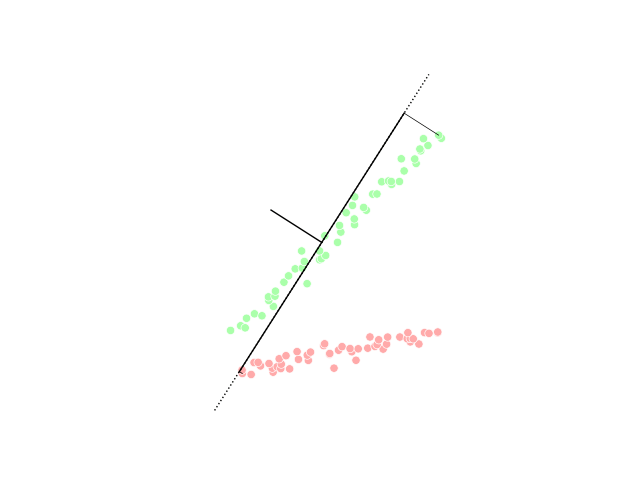
Искусство понижения размерности как раз состоит в том, чтобы выбрать такие проекции исходного датасета, чтобы максимально сохранить информацию об исходном распределении или разделение данных по классам:
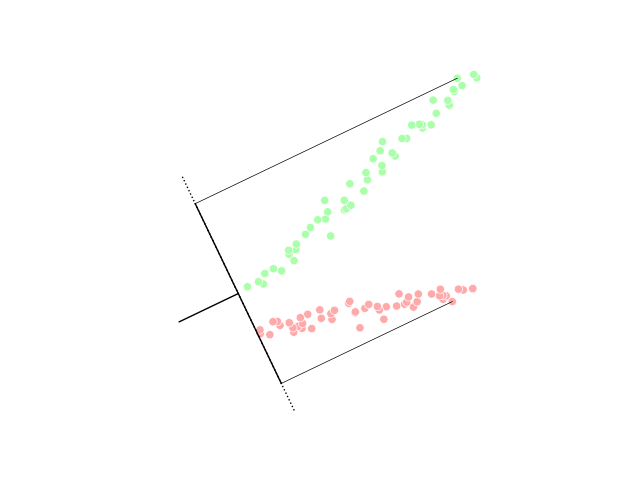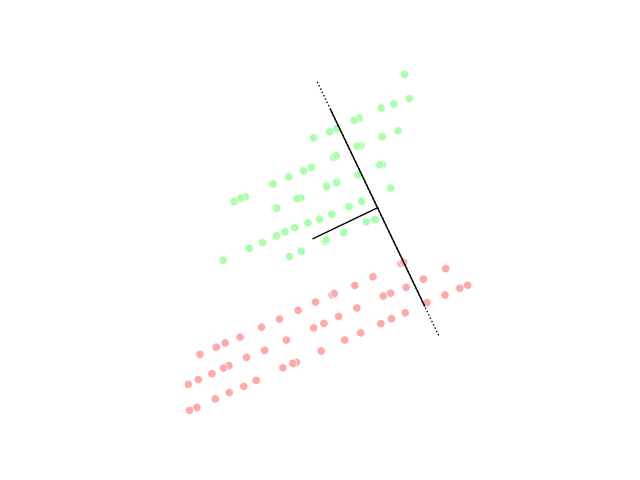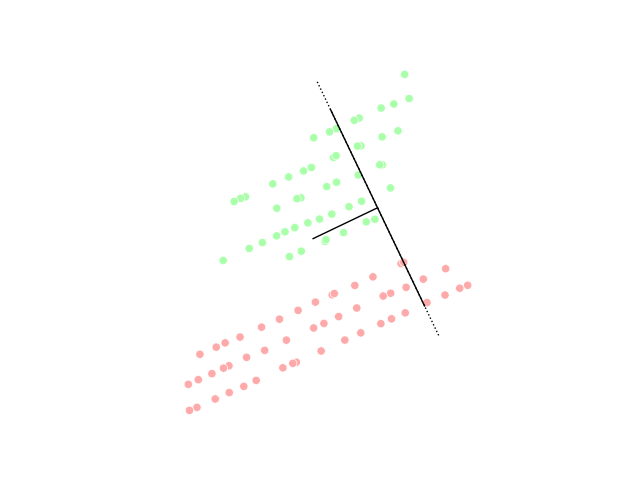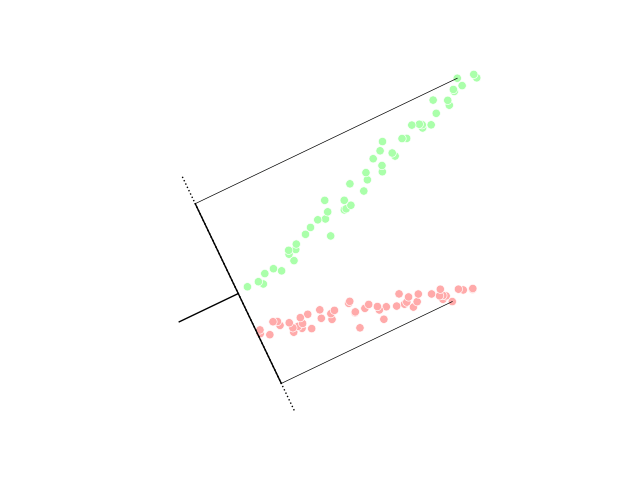
Существует различные методы понижения размерности. Выбор признаков сам по себе является методом понижения размерности, так как эквивалентен проектции на исходные оси. Кроме этого выделяют линейные и нелинейные методы понижения размерности:
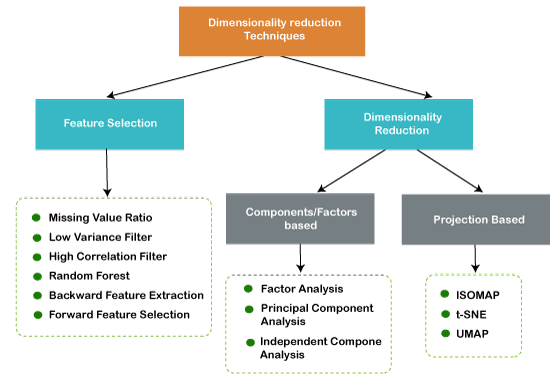
При этом надо помнить, что понижение размерности как правило свзано с потерей информации об исходном датасете. Чем большее сокращение произвести, тем больше информации теряется. Поэтому выбор количества измерений тоже представляет собой нетривиальную задачу. Как правило, для методов понижения размерности мы сами задаем желаемое количество измерений.
Например, для визуализации многомерных данных часто применяют понижение до 2 измерений. В таком случае можно получить максимально информативные, но все еще наглядные графики.
Выводы:
- Понижение размерности - нахождение самого информативного представления данных с меньшим количеством признаков.
- Проклятье размерности - чем больше признаков, тем экспоненциально больше нужно точек данных для формирования неразреженного множества.
- Может использоваться для визуализации данных - приведение к двум измерениям.
- Полезно для отбора и инжиниринга признаков и снижения вычислительной сложности обработки данных.
- Имеет дополнительный эффект очищения данных от шума.
- Существуют линейные и нелинейные методы.
- Отбор признаков сам по себе работает как понижение размерности.
- Признаки после понижения размерности становятся, как правило, неинтерпретируемые.
- Чем больше измерений оставить, тем больше информации сохраняется. Выбор - методом локтя.
PCA
Наиболее популярным алгоритмом сокращения размерности является метод главных компонент (principal component analysis, PCA). В этом методе переменные преобразуются в новый набор переменных, которые являются линейной комбинацией исходных переменных. Эти новые переменные известны как основные или главные компоненты. Они получаются таким образом, что первая компонента учитывает большую часть возможного изменения исходных данных, после чего каждая последуюая компонента имеет максимально возможную дисперсию.
Вторая главная компонента должна быть ортогональна первой. Другими словами, он делает все возможное, чтобы зафиксировать дисперсию данных, которые не были захвачены первым основным компонентом. Для двумерного набора данных могут быть только два главных компонента.
Учитывая две функции: $x_1$ и $x_2$, мы хотим найти одну такую переменную, которая эффективно описывает обе функции одновременно. Затем мы сопоставляем наши старые функции с этой новой строкой, чтобы получить новую отдельную функцию. То же самое можно сделать с тремя функциями, где мы сопоставляем их с плоскостью.
Цель PCA - уменьшить среднее значение всех расстояний каждой функции до линии проецирования. Это называется ошибка проецирования. Либо можно анализировать процент исходной дисперсии данных, который сохранился после уменьшения размерности:
Векторы главных компонент могут быть найдены как решения однотипных задач оптимизации:
Централизуются данные (вычитанием среднего): $x_i := x_i - \bar{X}$. Теперь $\sum_{i=1}^m = 0$;
Отыскивается первая главная компонента как решение задачи: $a_1 = argmin (\sum_{i=1}^m || x_i - a_1(a_1, x_i) ||^2)$. если решение не единственно, то осуществляется выбор одного из них.
Из данных вычитается проекция на первую главную компоненту: $x_i := x_i - a_1(a_1, x_i)$.
Отыскивается вторая главная компонента как решение задачи: $a_2 = argmin (\sum_{i=1}^m || x_i - a_2(a_2, x_i) ||^2)$. Если решение не единственно, то выбирается одно из них.
Далее процесс продолжается итеративно.
Смысл первой главной компоненты в том, что это такое направление, вдоль которого дисперсия исходного датасета максимальна:
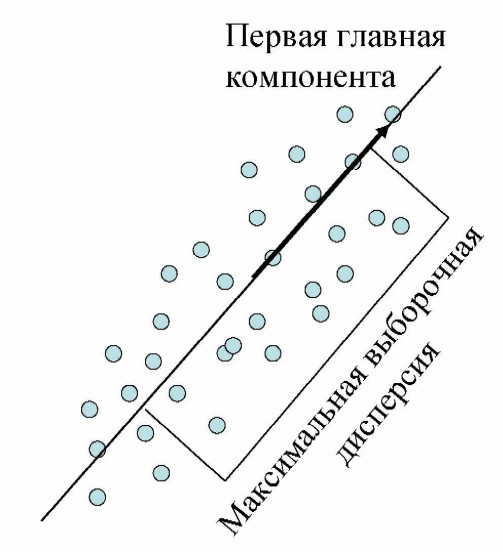
Поэтому если спроецировать точки данных на это направление, это максимально сохранит информацию о взаимном их расположении.
После окончания работы метода PCA можно выбрать столько компонент, сколько необходимо. Берутся последовательно компоненты, начиная с главной. Таким образом можно получить проекцию исходного датасета на любое количество измерений:
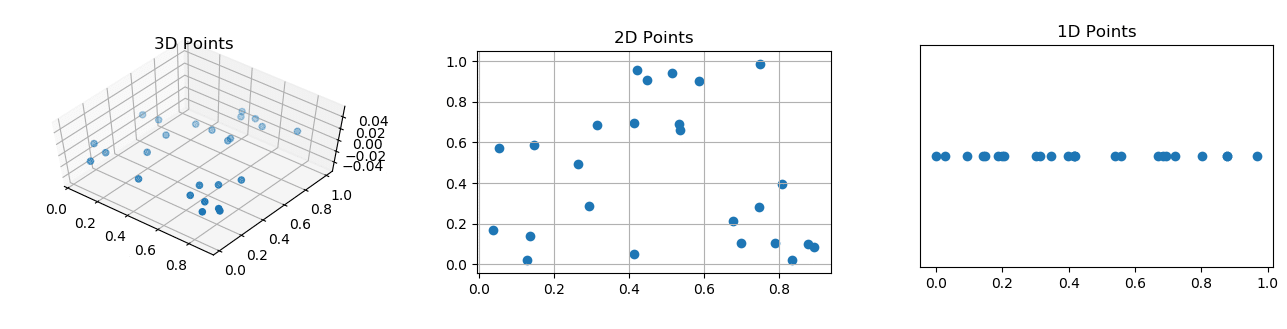
Иногда нужное количество измерений естественно следует из постановки задачи. В остальных случаях требуется выбрать количество измрений. Нужно понимать компромисс - чем больше измерений оставить, тем больше информации сохранится, но тем меньше смысла в преобразовании. Чем сильнее понизить размерность, тем больше информации теряется, но датасет становится компактнее. Можно воспользоваться
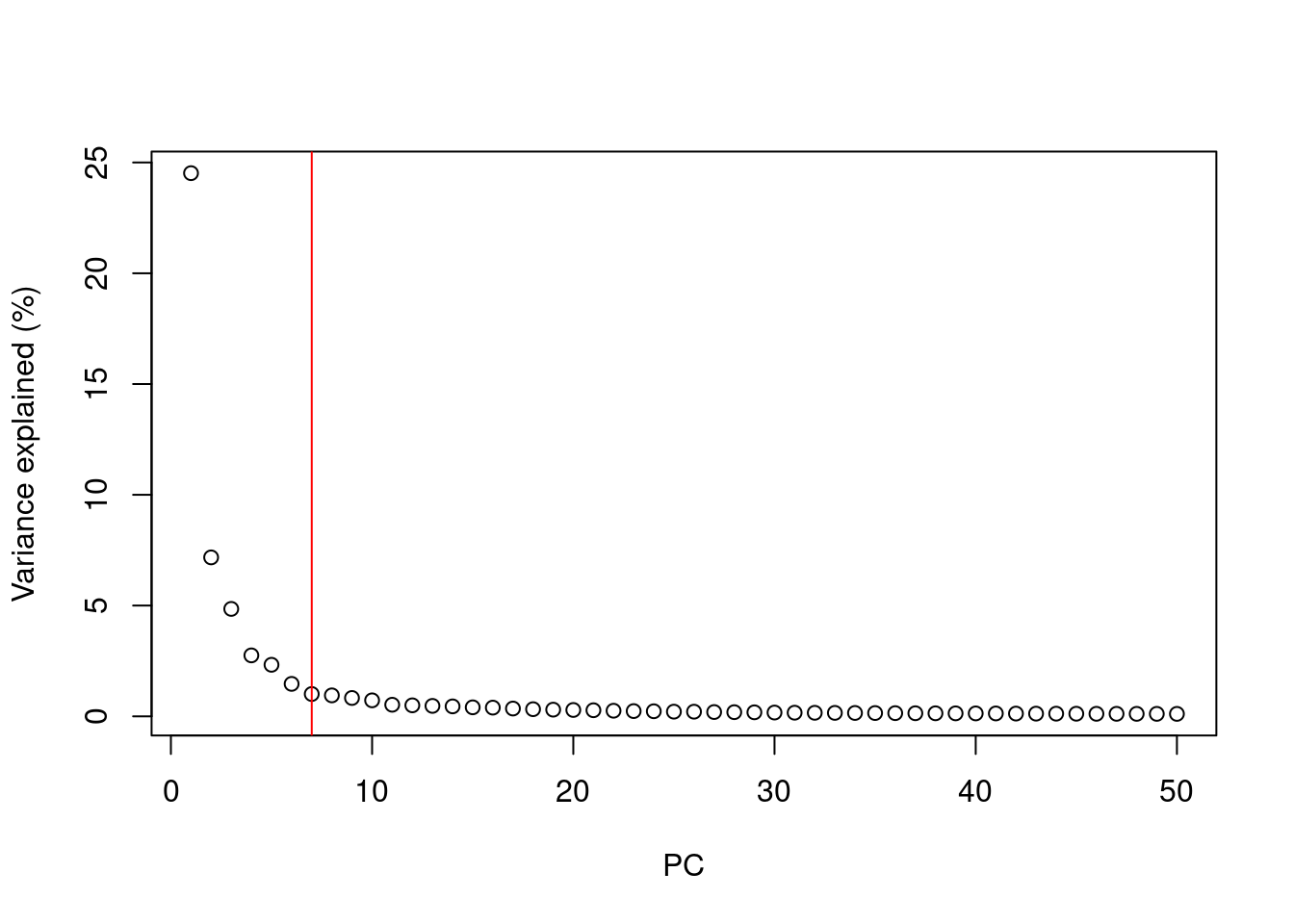
PCA не является линейной регрессией. В линейной регрессии мы минимизируем квадрат ошибки от каждой точки до нашей линии предиктора. Это вертикальные расстояния. В PCA мы минимизируем кратчайшее расстояние или кратчайшие ортогональные расстояния до наших точек данных. В более общем плане, в линейной регрессии, мы берем все наши примеры в x и применяем параметры в $b_i$ для предсказания y. В PCA мы берем ряд функций и находим среди них наиболее близкий общий набор данных. Мы не пытаемся предсказать какой-либо результат, и мы не применяем к ним веса.
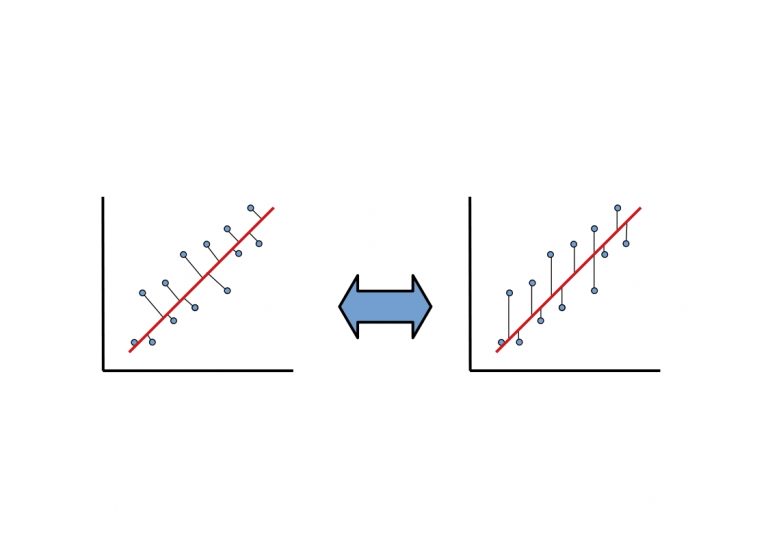
Рассмотрим применение метода PCA в Python на примере сгенерированного датасета:
1
2
3
4
5
6
7
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=500, noise=0.02, random_state=417)
plt.scatter(X[:, 0], X[:, 1], c=y)
plt.show()
Так выглядит исходный датасет:

Создадим и обучим простой метод главных компонент:
1
2
3
4
5
6
7
8
9
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
plt.title("PCA")
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y)
plt.xlabel("Component 1")
plt.ylabel("Component 2")
plt.show()
После преобразования мало что изменяется. Немного смещаются вектора проекции, что ведет к “наклону” исходного распределения:

Но метод главных компонент имеет нелинейную версию. Она импользует ядерные функции по аналогии с методом опорных векторов. Это позволяет делать проекции на нелинейные многообразия. Воспользуемся, например, радиально-базисной функцией:
1
2
3
4
5
6
7
from sklearn.decomposition import KernelPCA
kpca = KernelPCA(kernel='rbf', gamma=15)
X_kpca = kpca.fit_transform(X)
plt.title("Kernel PCA")
plt.scatter(X_kpca[:, 0], X_kpca[:, 1], c=y)
plt.show()
Это уже приводит к совершенно другому проеобразованию:

Выводы:
- Метод главных компонент последовательно выделяет векторы для проекции данных в исходном пространстве.
- PCA находит линейное представление с максимизацией выборочной дисперсией.
- Существует нелинейная версия - ядерный метод клавных компонент.
- Необходимо задавать количество компонент. Можно выбирать методом локтя.
- После преоразования признаки теряют предметный смысл.
- PCA проводит внутреннюю нормализацию данных. После снижения признаки тоже будут нормализованы.
ICA
Выводы:
Случайная проекция
NMF
T-SNE
Выводы:
UMAP
Обнаружение аномалий
Обнаружение аномалий - это задача машинного обучения, которая заключается в идентификации объектов обучающей выборки, который по совокупности своих характеристик существенно (статистически значимо) отличаются от основного большинства остальных объектов.
Под аномалией понимается некий объект, который сильно отличается от “нормы”, отклонение, исключение, редкое событие, которое не вписывается в общую зависимость, паттерн. Аномальные объекты часто свидетельствуют о нарушении каких-то зависимостей, подозрительных объектах.

Различают следующие типы аномалий:
- Глобальные аномалии
- Контекстуальные выборосы
- Коллективные выбросы
Когда значение точки данных выходит далеко за пределы всех других диапазонов значений точек данных в наборе данных, это можно рассматривать как глобальную аномалию. Другими словами, это редкое событие. Например, если вы ежемесячно получаете на свои банковские счета среднюю зарплату, но в один прекрасный день получаете миллион долларов, это будет выглядеть как глобальная аномалия для аналитической команды банка.
_(1).png)
Контекстуальный выброс, это такой у которого значение не соответствует тому, что ожидается для аналогичной точки данных в том же контексте. Контексты обычно являются временЫыми, и одна и та же ситуация, наблюдаемая в разное время, может не быть выбросом. Например, для магазинов вполне нормально наблюдать увеличение числа покупателей в праздничный сезон. Однако, если внезапный всплеск происходит вне праздничных дней или распродаж, это можно рассматривать как контекстуальное отклонение.
_(1).png)
Коллективные выбросы - это множество точек, которые отличаются от нормального поведения. В целом, технологические компании, как правило, становятся все больше и больше. Некоторые компании могут приходить в упадок, но это не общая тенденция. Однако, если многие компании одновременно демонстрируют снижение выручки за один и тот же период времени, мы можем выявить коллективный выброс.
_(1).png)
Обнаружение аномальных объектов может быть полезно в разных предметных областях. Например, анализ сетевой активности на предмет аномалий может указать на потенциальные атаки на сетевую инфораструктуру компании. Вот еще несколько примеров полезных предметных областей, которые могут быть сформулированы как поиск аномальных объектов:
- DDOS-атаки и другие угрозы сетевой инфраструктуры
- Инциденты информационной безопасности
- Мошеннические банковские операции
- Предаварийное состояние производственного оборудования
- Патологические медицинские состояния
- Критические события на финансовых рынках
Ключевой характеристикой аномалий является их редкость. Если аномальное поведение объектов встречается часто, это уже не может считаться аномалией. Поэтому при использовании алгоритмов обучения с учителем (классификации) существенная проблема дисбаланса классов. Аномальный объект вполне может встретиться на 10 000 или даже миллион нормальных объектов.
Поэтому хотя классические методы классификации, такие как KNN или SVM могут применяться для обнаружения аномалий, они не очень эффективны.
Нахождение аномалий в датасете с произвольным количеством признаков может быть не так тривиально, как могло бы показаться. Ведь большое количество признаков соответствует большому числу измерений. А объект может быть выборосом не по значению одного или пары признаков в отдельности, а по совокупности харкактеристик:
Алгоритм DBSCAN, который применяется для определения кластеров может также указать на аномалии. В этом алгоритме - это точки шума, которые не попали ни в один кластер:
Среди специфических методов обучения без учителя, предназначенных именно для обнаружения аномалий, следует выделить метод локального уровня выброса. Он основан на оценке локальной плотности точек в окрестностях каждой точки выборки. Если плотность точек в окрестностях какой-то конкретной точки сравнима с его соседями, либо больше, это свидетельствует о наличии плотной области. А если плотность вокруг данной точки существенно меньше, чем у соседей, это говорит о потенциальном наличии выброса.
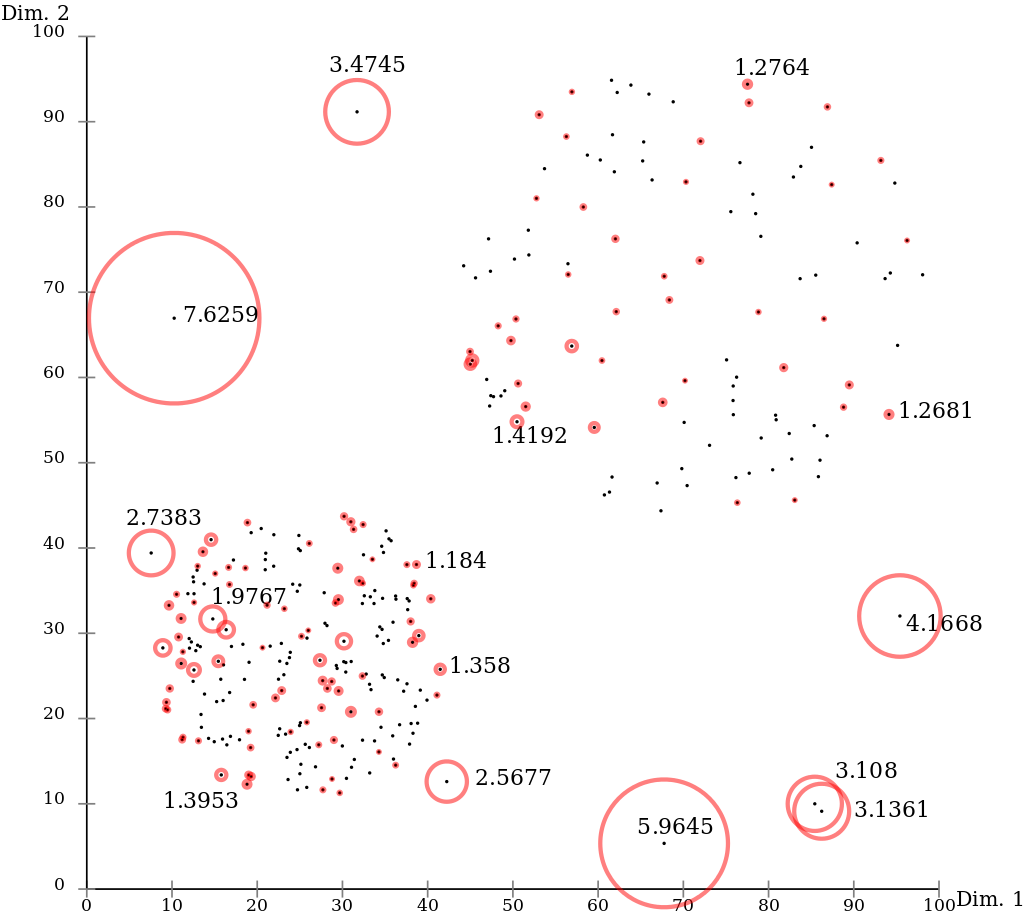
Вот пример применения этого метода в бибилиотеке sklearn в Python:
1
2
3
4
5
6
from sklearn.neighbors import LocalOutlierFactor
clf = LocalOutlierFactor(n_neighbors=20, contamination=0.1)
y_pred = clf.fit_predict(X)
n_errors = (y_pred != ground_truth).sum()
X_scores = clf.negative_outlier_factor_
Выводы:
- Обнаружение аномалий - это алгоритм идентификации объектов выборки, значимо отличающихся от остальных.
- Аномалии могут иметь разную природу, но общая черта - редкость.
- Обнаружение аномалий обучением с учителем сложно из-за дисбаланса классов.
- Обнаружение аномалий в пространствах высоких размерностей сложно и неочевидно.
- Аномалии свидетельствуют о подозрительных объектах. Их обнаружение ценно во многих областях.
- Удаление аномальных объектов может быть этапом подготовки и очистки данных.
- Среди популярных методов обнаружения аномалий - метод локального уровня выброса