Линейная алгебра
В машинном обучении мы часто сталкиваемся с понятиями вектора и матрицы. Мы говорим о матрице признаков, то есть сам набор данных представляет собой матрицу. Одну колонку в этом датасете мы называем “вектором признака”. И каждую точку данных, то есть объект предметной области, которую мы анализируем, мы часто представляем именно как точку, то есть вектор, в некотором пространстве.
Более того, сами уравнения и модели в машинном обучении очень часто представляются в матричном виде. То есть они оперируют не над числами и переменными, а над списками и таблицами чисел. В таком виде соотношения и алгоритмы записываются гораздо проще. Поэтому для полноценного изучения машинного обучения не обойдешься без подробного разговора о векторах, матрицах, их смысле и операциях над ними.
Раздел математики, который занимается операциями над векторами и матрицами называется линейной алгеброй. Алгебра - это потому, что здесь вводятся математические операции над этими специальными объектами. А линейна она потому, что большинство этих операций соответствуют линейным преобразованиям некоторых пространств. В этом разделе учебника мы познакомимся с основными объектами линейной алгебры, операциями над ними. Также обратите свое внимание на общепринятые обозначения, так как они будут нас преследовать на всем протяжении изучения машинного обучения.
Вектор
Центральным элементом линейной алгебры, ее самым базовым понятием является вектор. Вектор можно определять разными способами. Мы здесь приведем три определения вектора - геометрический, алгоритмический и алгебраический. Для нас будет важно понять не только все три подхода по отдельности, но и то, как они соотносятся между собой. Именно в этом пересечении трех разных аспектов и находится истинное определение вектора.
Для алгоритмиста - вектор это всего лишь упорядоченный список чисел. Каждое число, составляющее вектор - это компонента. Вектор может состоять из одной, двух, трех компонент, из какого угодно числа компонент. С этой точки зрения вектор мало чем отличается от простого списка. Единственное ограничение - мы рассуждаем именно о списках чисел.
Вот так обозначается математически вектор:
\[\vec x = \begin{bmatrix} 2 \\ 5 \end{bmatrix}\]Мы имеем вектор, состоящий из двух компонент. Первая компонента равна 2, вторая - 5. В общем случае, вектор может состоять из произвольного числа компонент. Назовем число компонент нашего вектора - $n$. В таком случае, он будет обозначаться так:
\[\vec x = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}\]Заметьте, что традиционно компоненты вектора записываются именно в столбец. Для компактности мы можем иногда записывать вектор как простой список, в строчку: $\vec x = [ x_, x_2, \dots, x_n ]$. Позже, когда мы будем говорить о матрицах, для нас в некоторых контекстах будет важна разница между вектором-столбцом и вектором-строкой. Но сейчас опустим технические детали.
Для геометра вектор - это некоторый объект, имеющий величину и направление. Именно в геометрическом смысле вектора часто визуализируются как стрелки на графике. Вот как они выглядят на двумерной плоскости:
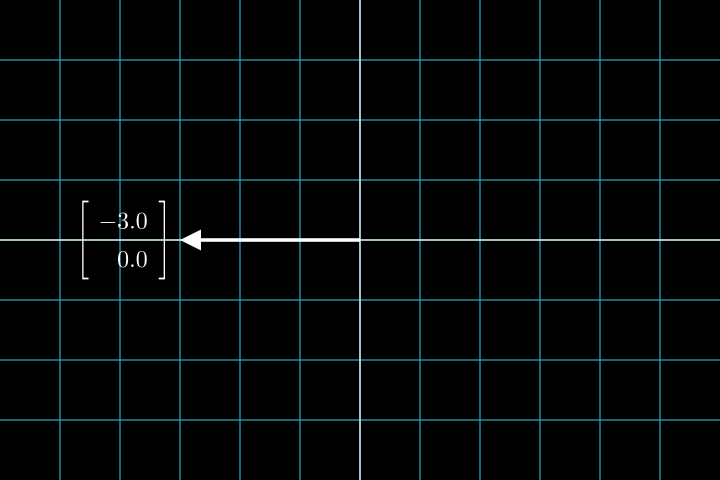
В данном случае (по общепринятому соглашению), первая компонента вектора представляет собой его длину в горизонтальном направлении. Вторая - в вертикальном. В итоге вектор рисуется как отрезок, имеющий начало в начале координат, а конец (стрелка) - в соответствующей точке.
Важное замечание, что в такой формулировке вектора не имеют смысла без определения системы координат. Именно поэтому на рисунке мы сначала нарисовали координатную сетку, а уже внутри нее - вектора. Это будет важно позднее, когда мы будем говорить о базисах.
Но нужно понимать, что такая стрелка является лишь представлением некоторого направления и величины. Именно поэтому она традиционно всегда начинается в начале координат. Если сдвинуть стрелку так, чтобы ее направление и длина не менялась, но она начиналась из другой точки, то математически это будет тот же самый вектор:
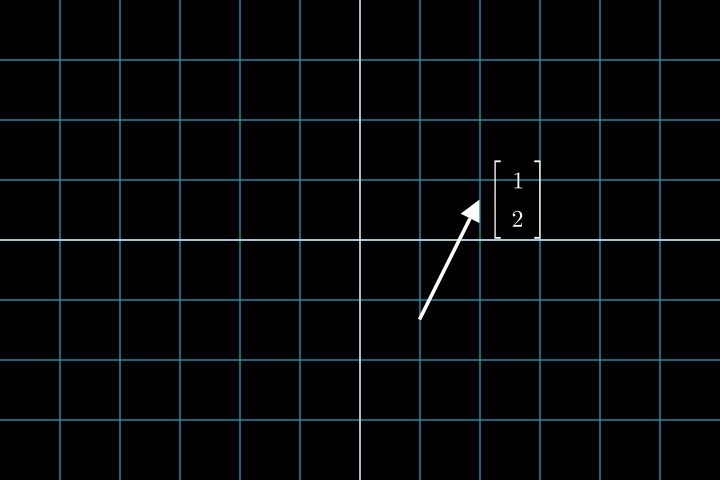
На самом деле не важно, как именно мы рисуем вектор. Это лишь графическое представление, которое помогает нам справиться с интуитивным пониманием векторных концепций. На самом деле, вектор однозначно задается своими компонентами. В нем нет ничего сверх того.
Можно например, представлять себе вектор, как задающий некоторый параллельный перенос. То есть вектор - это формализация того, в какую сторону и на сколько мы перенесли что-то на координатной плоскости. В таком случае, не важно, из какой точки мы начали, вектор задает лишь направление и величину.
И мы видим это на графике. Разные стрелки соответствуют разным значениям компонентов вектора. Если мы изменяем значение компонента, то стрелка на графике перемещается (то есть перемещается ее конец). То есть сам вектор меняет либо длину, либо направление, либо и то и другое. То есть значение компонентов вектора однозначно задает нам вектор.
И наоборот, если мы выберем произвольную точку на координатной плоскости, то, соединив ее в центром координат, мы получим некоторый вектор. Его компоненты будут однозначно задаваться координатами этой точки. Поэтому вектора можно вообще не изображать стрелками - можно оставить только саму точку:
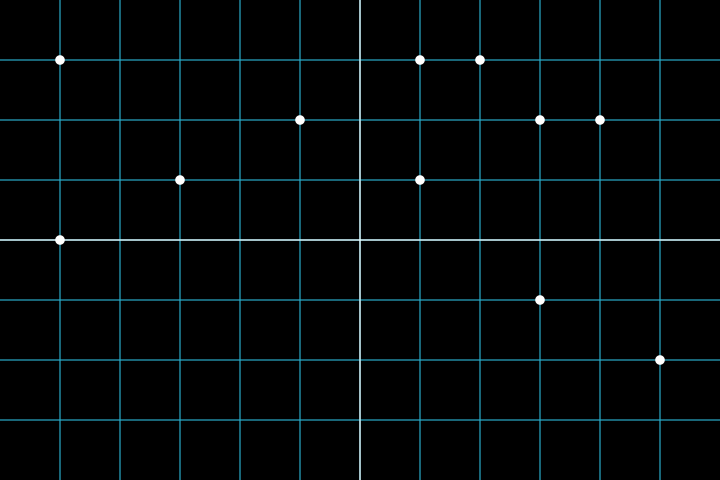
Такой прием будет полезен, если, например, на графике очень много векторов. Стрелки загромождают его и делают трудно воспринимаемым. Например, если мы рассматриваем совокупность векторов, концы которых лежат на некоторой линии (в данном случае прямой), можно вообще не рисовать эти стрелки, а оставить саму линию:
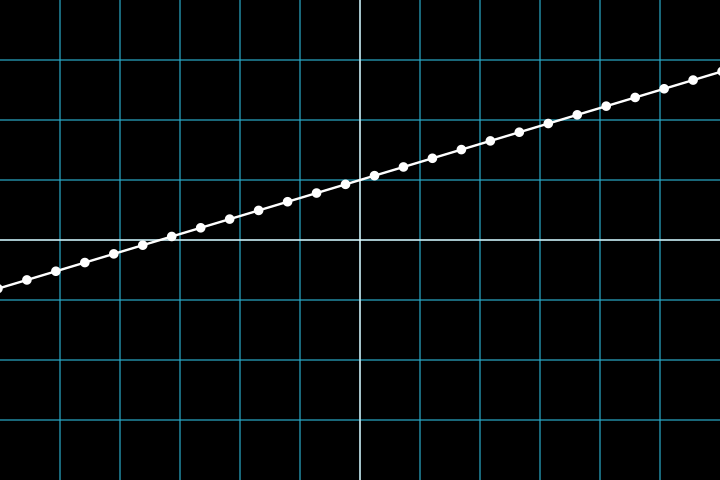
Но важно то, что по сути, вектор и точка в некотором пространстве - это одно и то же. Поэтому часто эти два понятия используют взаимозаменяемо. Например, в анализе данных можно слышать термин “точка данных”. Почему это точка? Потому, что это список чисел, то есть вектор. А вектор всегда можно представить в виде точки в некотором пространстве.
Здесь удобно ввести еще одно обозначение, которое нужно знать для работы с линейной алгеброй. Мы говорим, что вектор - это точка в некотором пространстве. А это это за пространство? Каждая компонента вектора - это число. Поэтому если у вектора всего одна компонента, его можно представить как точку на числовой прямой. В таком случае, пространство - это множество действительных числе, или как его обозначают в математике - $\mathbb{R}$. То есть можно сказать, что такой вектор принадлежит (является элементом)множества действительных чисел: $\vec x \in \mathbb{R}$.
А если компонента два? Тогда, как мы видели на графике, вектор - это точка на числовой плоскости. Плоскость - это совокупность двух числовых прямых. Плоскость - это совокупность всех возможных комбинаций двух координат. А совокупность всех комбинаций - это определение декартова произведения множеств. Поэтому, координатная плоскость определяется так: $\mathbb{R} \times \mathbb{R} = \mathbb{R}^2$.
Ну а в общем случае, когда у вектора $n$ компонентов, его можно записать так:
\[\vec x \in \mathbb{R}^n\]Эта запись означает, что n-компонентный вектор является точкой (элементом) n-мерного пространства. Потому вектор, состоящий из, например, двух компонент, называют двумерным вектором. Это и проще, и короче, и отражает суть и смысл этого вектора.
Другими словами, компоненты вектора соответствуют измерениям в пространстве. Можно говорить об одномерных векторах, двумерных, пятимерных. У вектора может быть пятнадцать измерений или даже сто тысяч. Не обязательно представлять себе вектор визуально, чтобы понимать, как он работает. Но для начала это визуальное представление будет очень полезно:
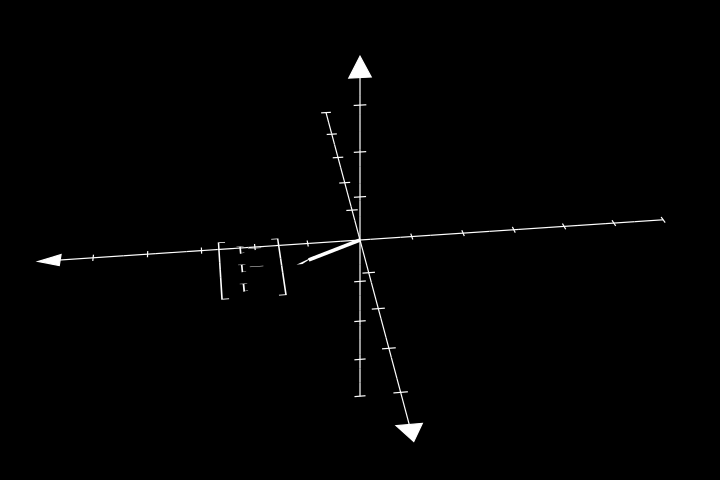
В дальнейшем мы будем в основном рисовать вектора именно в двумерном пространстве. Это гораздо проще и реализовать, и воспринимать. Но вы всегда должны помнить, что вектор может быть любой мерности. Рассматривая каждую визуализацию из этого учебника, представляйте себе, как показанный принцип обобщается на произвольное количество измерений.
Почему вектора так распространены в машинном обучении? Потому, что в нем очень много используется анализ данных. А анализ данных имеет дело с информацией со сложной структурой. Это в первую очередь значит, что данных много и их часто организую в виде списков.
Допустим, у нас есть набор данных о какой-то задаче. Он обычно состоит из списка (уже список) каких-то объектов. Например, датасет, содержащий характеристики объектов недвижимости. Каждый объект имеет некоторые свойства (в машинном обучении их часто называют атрибутами). Важно, что все объекты имеют одинаковые наборы атрибутов. Но разные значения.
В таком случае, каждый объект в наборе данных удобно представлять в виде вектора. Компонентами этого вектора будут выступать значения его характеристик. Если у объекта всего две характеристики, его можно представить как точку на плоскости. Например, у нас в наборе данных записана информация о площади объекта недвижимости и его стоимости. Вот как может выглядеть один вектор в данном наборе:
\[\vec{x} = \begin{bmatrix} 33 \\ 12 \end{bmatrix};\]Этот вектор представляет собой объект недвижимости площадью 33 квадратных метра и стоимостью 12 миллионов рублей. Другие объекты (строчки в нашем наборе данных) будут иметь другие значения, но такое же количество характеристик, то есть компонентов вектора.
Это значит, что все точки в датасете будут лежать в одном пространстве (в данном случае, $\mathbb{R}^2$). Это будет очень важно позднее, когда мы будем говорить об операциях над векторами. Это значит, что мы сможем их сравнивать, оценивать близость, а далее - выделять классы, кластеры, находить внутреннюю структуру в этих данных.
Именно поэтому, кстати, вектор - это именно упорядоченный набор чисел. На абстрактной координатной плоскости можно понять, что два вектора этих вектора разные:
\[\vec x = \begin{bmatrix} 2 \\ 5 \end{bmatrix}; \vec y = \begin{bmatrix} 5 \\ 2 \end{bmatrix};\]Но при анализе реальных данных это становится очевидно:
\[\vec{квартира в центре} = \begin{bmatrix} 50 м^2 \\ 200 млн \end{bmatrix}; \vec{дом на окраине} = \begin{bmatrix} 200 м^2 \\ 50 млн \end{bmatrix};\]Поэтому важно для всех объектов набор данных соблюдать порядок перечисления характеристик. Иначе, данные будут составлять несообразные вектора. Поэтому набор векторов составляет таблицу, в которой каждый столбец - это определенная характеристика объекта. А таблицы у нас соответствуют еще более сложному математическому объекту - матрице. Но об этом позднее.
А что же такое вектор для алгебраиста? Это третий подход к определению понятия вектор. С этой точки зрения, вектор - это любой объект, для которого определены операции сложения и умножения на скаляр. То есть, как часто в математике (да и в компьютерных науках так бывает, вспомните типы данных), объект определяется через то, что можно с ним сделать.
Так что базовые операции над векторами тоже важны для понимания того, что это за объект. Действительно, пока мы только ввели новые обозначения, в них мало смысла. Надо понять, что они позволяют нам сделать. Поэтому сейчас рассмотрим эти две математические операции над векторами.
Умножение вектора на скаляр
Рассматривая базовые операции с векторами, мы сначала введем определения, а уже потом проанализируем, почему эти операции определяются именно так. Дело в том, что
Самая простая операция с векторами - умножение вектора на число. Для его выполнения каждая компонента вектора умножается на это самое число.
\[\vec x = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}; c \cdot \vec x = \begin{bmatrix} c \cdot x_1 \\ c \cdot x_2 \\ \vdots \\ c \cdot x_n \end{bmatrix};\]В отличие от перемножения двух чисел, когда множители являются полностью равноправными и их порядок не важен, в данном случае, мы имеем умножение разных по сути объектов. Поэтому важно подчеркнуть, что результатом умножения любого вектора на число является вектор той же размерности, то есть лежащий в том же пространстве.
Умножение вектора на число имеет очень простой и понятный геометрический смысл: масштабирование вектора. Посмотрите, как умножение на разные числа растягивает или сжимает вектор:
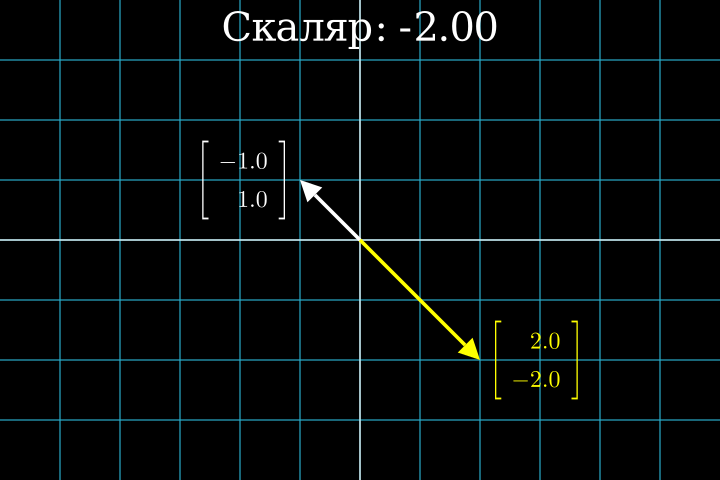
Умножение на число больше единицы как бы равномерно растягивает вектор. При этом, что важно, его направление не меняется, а вот длина увеличивается пропорционально этому числу. Число в этой операции играет роль как бы коэффициента масштабирования (scaling), поэтому его часто называют “скаляр”. Этот термин подчеркивает роль числа в векторной алгебре при выполнении умножения.
Легко увидеть, что умножение на единицу никак не меняет исходный вектор:
\[1 \cdot \vec x = \begin{bmatrix} 1 \cdot x_1 \\ 1 \cdot x_2 \\ \vdots \\ 1 \cdot x_n \end{bmatrix} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \vec x;\]В этой операции особая роль единицы такая же, как и при классическом умножении (именно поэтому, кстати, эа операция и называется “умножением”, а не как-то иначе, “масштабированием”, например). Также очевидно, что умножение на ноль превращает любой вектор в нулевой, то есть в точку, совпадающую с началом координат:
\[0 \cdot \vec x = \begin{bmatrix} 0 \cdot x_1 \\ 0 \cdot x_2 \\ \vdots \\ 0 \cdot x_n \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix};\]В линейной алгебре, то есть в операциях над векторами, такой нулевой вектор играет ту же роль, что и ноль в обычной арифметике. Это мы увидим чуть позже.
Умножение на число больше нуля, но меньше единицы, не “растягивает”, а “сжимает” вектор. Его направление также не меняется, а длина уменьшается.
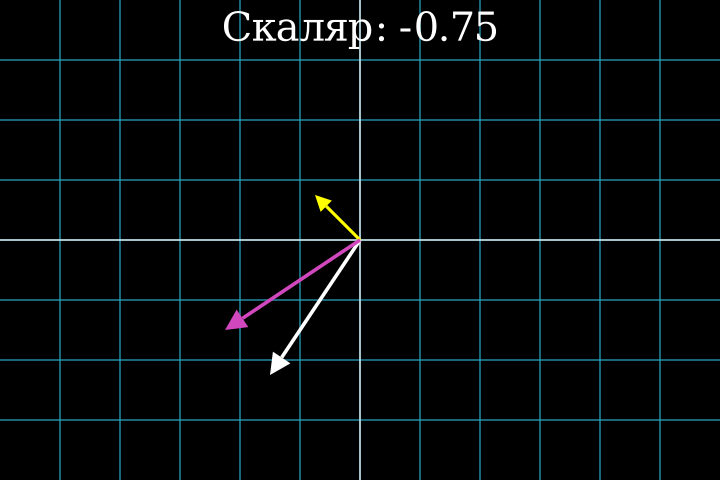
А вот умножение на отрицательное число уже меняет направление вектора. Причем строго на противоположное относительно начала координат. Вектор теперь смотрит в другую сторону, а его длина также увеличивается или уменьшается пропорциональной величине скаляра.
Обратите внимание, что если зафиксировать изначальный вектор, и изменять скаляр, то можно получить любой вектор, который лежит на той же прямой, что и исходный. То есть множество всех векторов, которые можно получить из данного умножением на скаляр, представляет собой прямую, проходящую через начало координат и конец данного вектора.
Сложение двух векторов
Еще более интересна операция сложения двух векторов. Оговоримся сразу, что складывать можно только те вектора, которые находятся в одном пространстве. То есть для существования суммы нужно, чтобы вектора имели одинаковое количество компонентов. Нельзя сложит двумерный вектор с трехмерным. Таких ограничений в линейной алгебре еще много. В обычной арифметике такого не встретить, ведь все объекты там равноправны. Фактически, все обычные числа - это скаляры с точки зрения линейной алгебры.
Но если размерность векторов совпадает, то их сумма определяется как вектор, каждый компонент которого является суммой соответствующих компонентов исходных векторов:
\[\vec x + \vec y = \begin{bmatrix} x_1 + y_1 \\ x_2 + y_2 \\ \vdots \\ x_n + y_n \end{bmatrix};\]И вновь, это не просто логичное определение само по себе, у него есть очень понятная геометрическая интерпретация. Представьте себе, что второй вектор можно поставить на “конец” первого. Тогда сумма векторов - это вектор, соединяющий начало координат с концом второго вектора:
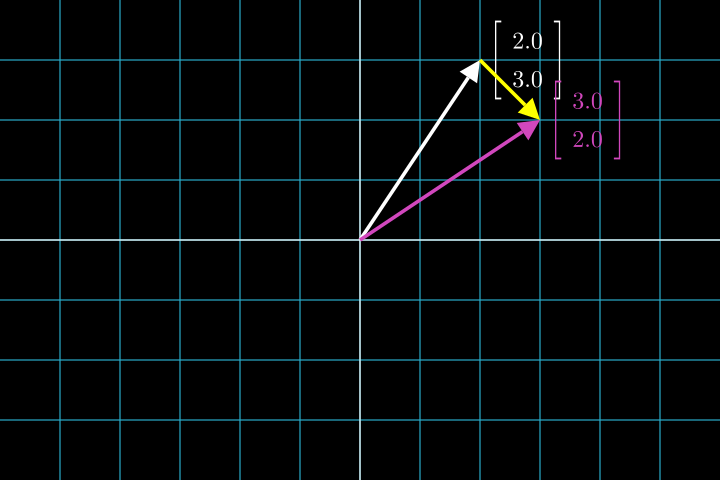
Когда мы разберемся, что такое базис, объяснение смысла суммы станет еще более очевидно. Сейчас скажем пару слов о том, как работает сложение векторов.
Во-первых, вспомним особый случай вектора, про который мы говорили в предыдущем пункте: нулевой вектор. Очевидно, что сложение нулевого вектора с любым даст тот же самый вектор:
\[\vec{0} + \vec x = \begin{bmatrix} 0 + x_1 \\ 0 + x_2 \\ \vdots \\ 0 + x_n \end{bmatrix} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \vec x;\]В этом смысле нулевой вектор в линейной алгебре играет ту же роль, что и ноль в обычной арифметике. То есть он при сложении никак не влияет на другое слагаемое.
Еще одно знакомое свойство сложения - коммутативное (переместительное) - для векторов также выполняется. Численно это тоже очевидно:
\[\vec x + \vec y = \begin{bmatrix} x_1 + y_1 \\ x_2 + y_2 \\ \vdots \\ x_n + y_n \end{bmatrix} = \begin{bmatrix} y_1 + x_1 \\ y_2 + x_2 \\ \vdots \\ y_n + x_n \end{bmatrix} = \vec y + \vec x;\]Но у этого свойства есть очень красивое геометрическое объяснение (этот принцип называется “правило параллелограмма”):
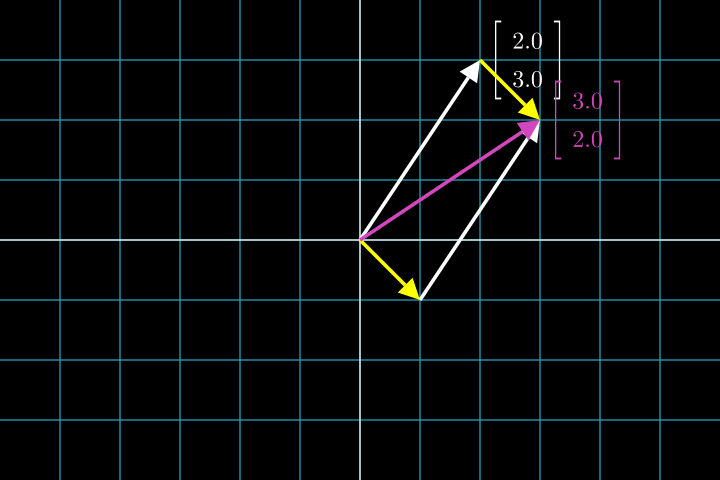
То есть мы можем переместить первый вектор к концу второго, или второй к концу первого - сумма от этого не меняется.
Кстати, именно из-за того, что для сложения векторов выполняются эти свойства, эту операцию, которую мы определили как сумму компонентов вектора и назвали сложением векторов. Оно работает как и обычное сложение для чисел.
Еще одно важное свойство операций над векторами также имеет аналог в обычной арифметике. Это дистрибутивное свойство умножения относительно сложения. Численно показать его также несложно:
\[с \cdot (\vec x + \vec y) = c \cdot ( \begin{bmatrix} x_1 + y_1 \\ x_2 + y_2 \\ \vdots \\ x_n + y_n \end{bmatrix}) = \begin{bmatrix} c \cdot (x_1 + y_1) \\ c \cdot (x_2 + y_2) \\ \vdots \\ c \cdot (x_n + y_n) \end{bmatrix} = \begin{bmatrix} c \cdot x_1 + c \cdot y_1 \\ c \cdot x_2 + c \cdot y_2 \\ \vdots \\ c \cdot x_n + c \cdot y_n \end{bmatrix} = c \cdot \begin{bmatrix} x_1\\ x_2 \\ \vdots \\ x_n \end{bmatrix} + c \cdot \begin{bmatrix} y_1\\ y_2 \\ \vdots \\ y_n \end{bmatrix} = c \cdot \vec y + c \cdot \vec x;\]По смыслу это правило тоже довольно легко понять, если вспомнить, что умножение на скаляр работает как масштабирование векторов. Для того, чтобы масштабировать сумму можно по отдельности масштабировать каждое слагаемое. И наоборот, если масштабировать каждое слагаемое по отдельности, это имеет такой же эффект, как если просто умножить на это же число сумму:
Вообще, на векторах определено еще множество разных операций. Есть поэлементное сложение, скалярное произведение, нормирование, десятки разных операций, один более распространены на практике, другие полезны только для очень специальных случаев. Но именно эти две являются определяющими.
Как мы говорили в первой части, вектор может быть определен как некоторый объект, на котором существуют операции сложения и умножения (причем именно с такими свойствами, которые мы определили). В таком смысле точка в пространстве - это вектор, список числе - тоже вектор. В математике многочлен, степенной ряд - тоже могут рассматриваться как вектора.
Ну а в анализе данных, как мы говорили, вектором можно воспринимать любой упорядоченный список. Мы уже упоминали вектор признаков объекта. Но также можно говорить, например, о векторе весов (параметров) модели. Являются ли все эти объекты на самом деле векторами? На самом деле, никакого “самого дела” нет. Что-то можно рассматривать как вектор, если это может быть полезно. Если операции и свойства векторов могут нам дать полезный инструмент анализа реального мира.
И как мы посмотрим в последующих главах, на приведенном определении вектора можно построить очень сложную конструкцию под названием “линейная алгебра”. И многие инструменты этой области математики применяются для анализа данных и построения моделей машинного обучения.

