Алгоритм обратного распространения ошибки

Модельная нейросеть

Здесь мы рассмотрим обратное распространение, основной алгоритм, лежащий в основе процесса обучения нейронных сетей. Если вы ознакомились с последними двумя уроками или у вас есть соответствующий опыт, вы знаете, что такое нейронная сеть и как она передает информацию.

Краткое изложение Мы рассмотрели классический пример распознавания рукописных цифр. Я показал сеть с…

• Входной слой состоит из 784 нейронов (которые представляют значения пикселей изображения)
• Два скрытых слоя по 16 нейронов в каждом
• Выходной слой с 10 нейронами (указывает на выбранную сетью цифру)

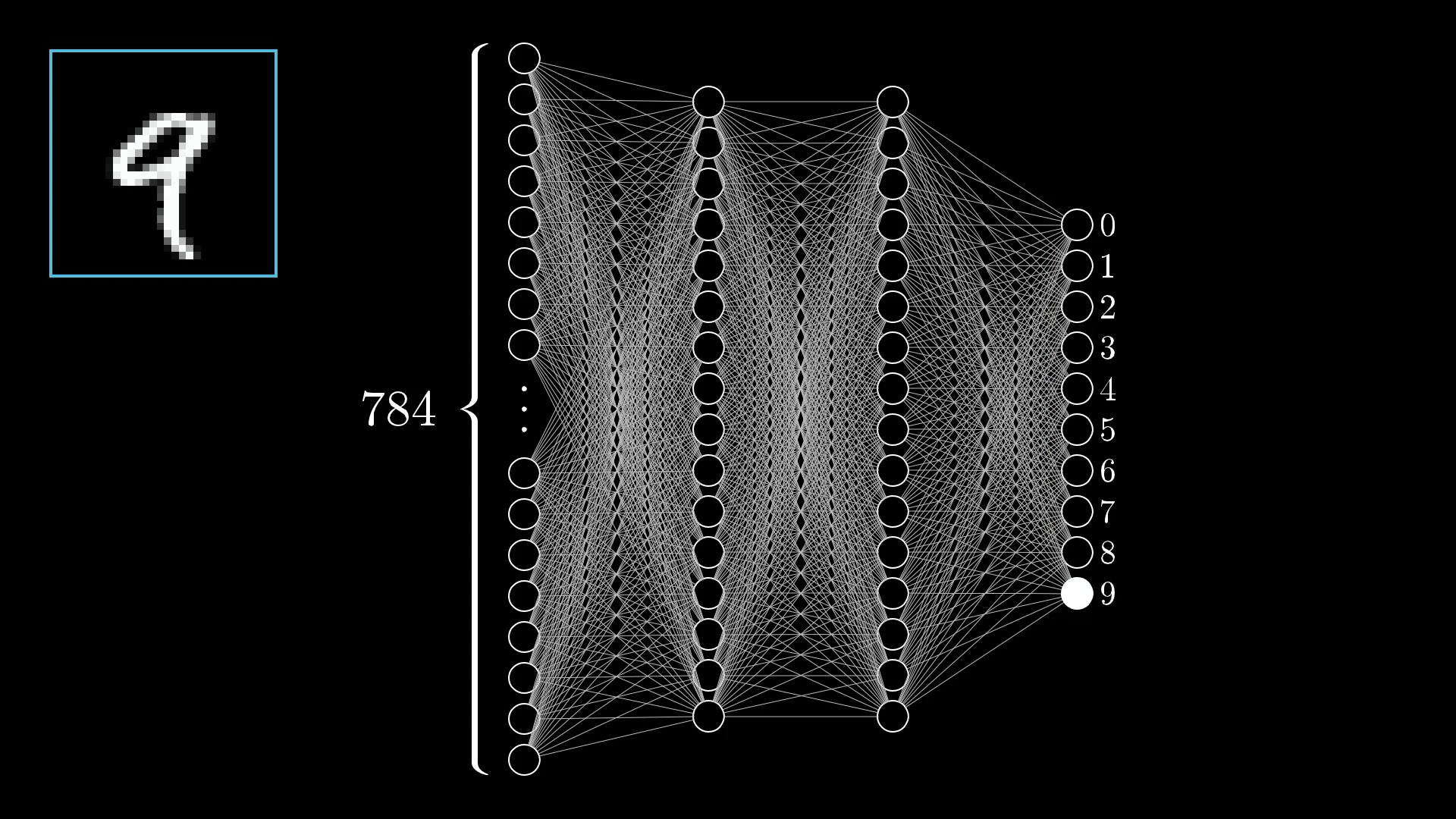
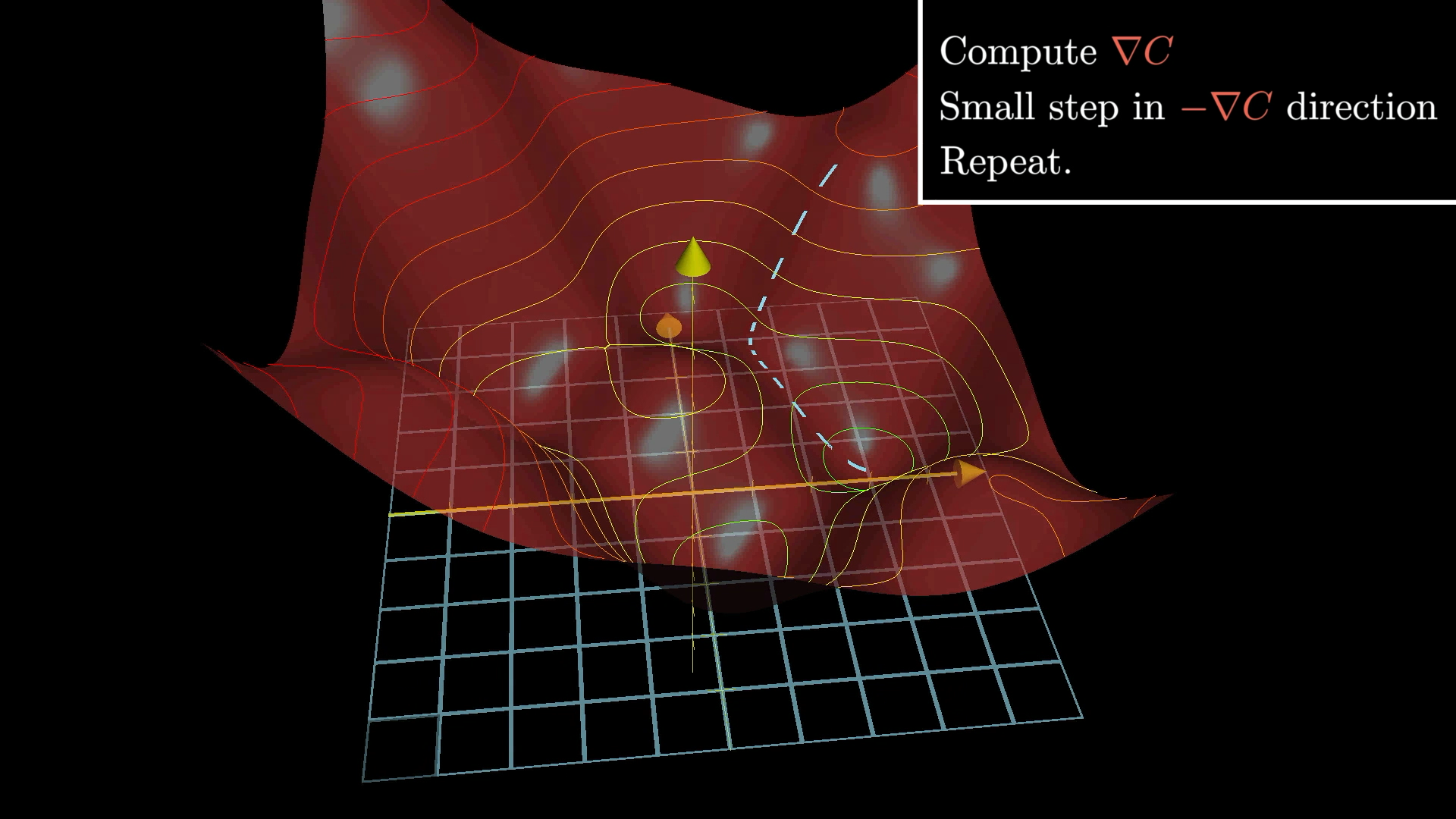
Мы также обсуждали градиентный спуск, поэтому вы должны знать, что когда люди называют сеть “обучающейся”, они имеют в виду нахождение весов и смещений, которые минимизируют определенную функцию затрат.

Чтобы рассчитать стоимость одного обучающего примера, вы берете выходные данные, которые выдает сеть, вместе с теми, которые вы хотели получить, и складываете квадраты различий между каждым компонентом:

Проделав это для всех десятков тысяч обучающих примеров и усреднив все результаты, вы получите общую стоимость сети.

Алгоритм обратного распространения ошибки

Помните, что отрицательный градиент функции затрат представляет собой 13 002-мерный вектор, который подсказывает нам, как использовать все веса и смещения для наиболее эффективного снижения затрат. Обратное распространение, тема этого урока, - алгоритм вычисления этого отрицательного градиента.

Представление о векторе градиента как о направлении в 13 002-мерном пространстве, мягко говоря, выходит за рамки нашего воображения.

Итак, как мы уже говорили на предыдущем уроке, полезно рассмотреть это следующим образом: величина каждого компонента градиента показывает, насколько функция затрат чувствительна к каждому соответствующему весу и смещению.

Например, предположим, вы вычисляете отрицательный градиент, используя процесс, который я собираюсь описать, и компонент, связанный с весом на одном ребре, оказывается равным 3,2, в то время как компонент, связанный с каким-либо другим ребром, равен 0,1:

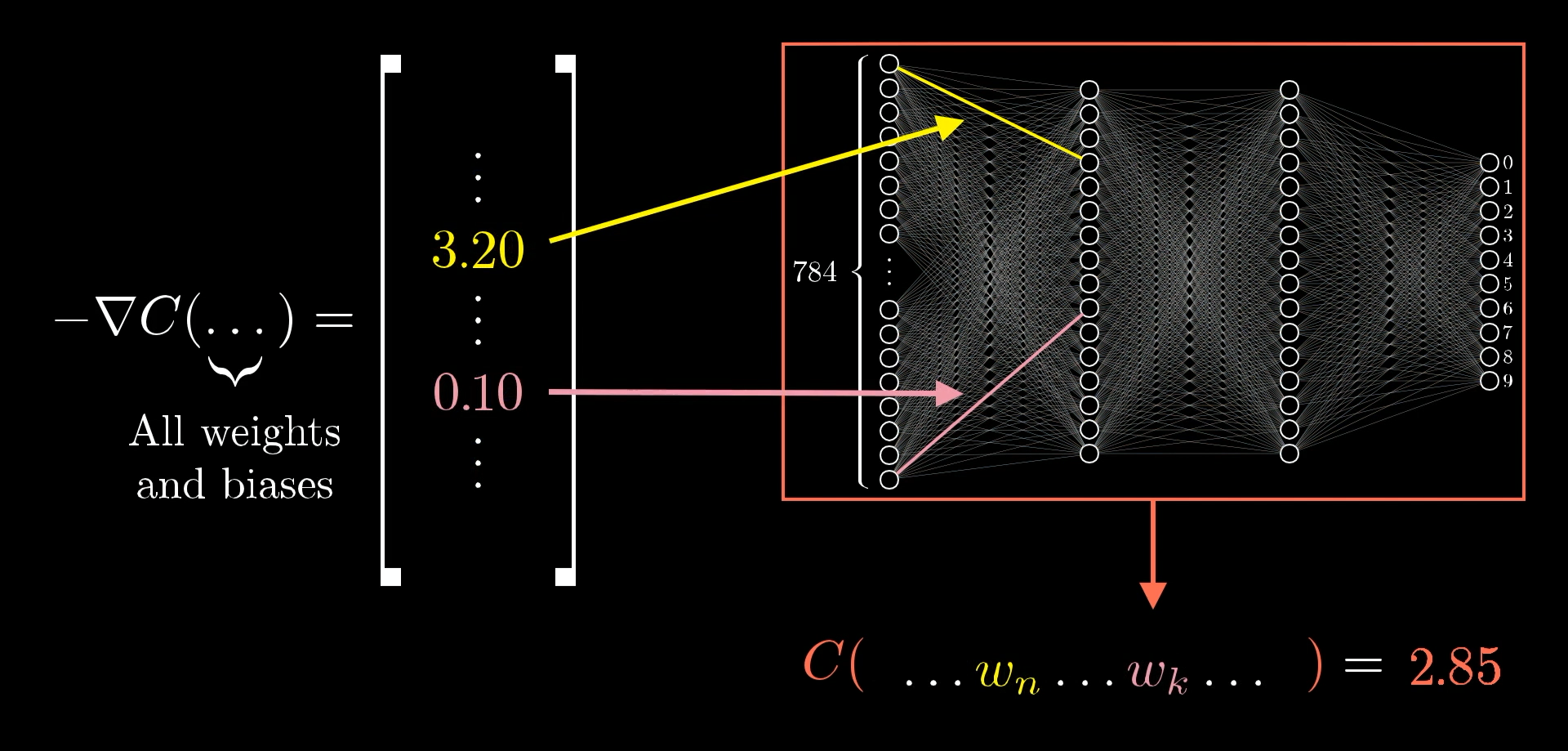
Из этого следует, что функция затрат в 32 раза более чувствительна к изменениям этого первого веса. Таким образом, если вы немного измените значение этого веса, это приведет к изменению функции стоимости в 32 раза большему, чем то, к чему привело бы такое же изменение второго веса.

Интуиция для обратного распространения

Когда я впервые изучал обратное распространение, самым запутанным аспектом было просто использование обозначений и индексов.

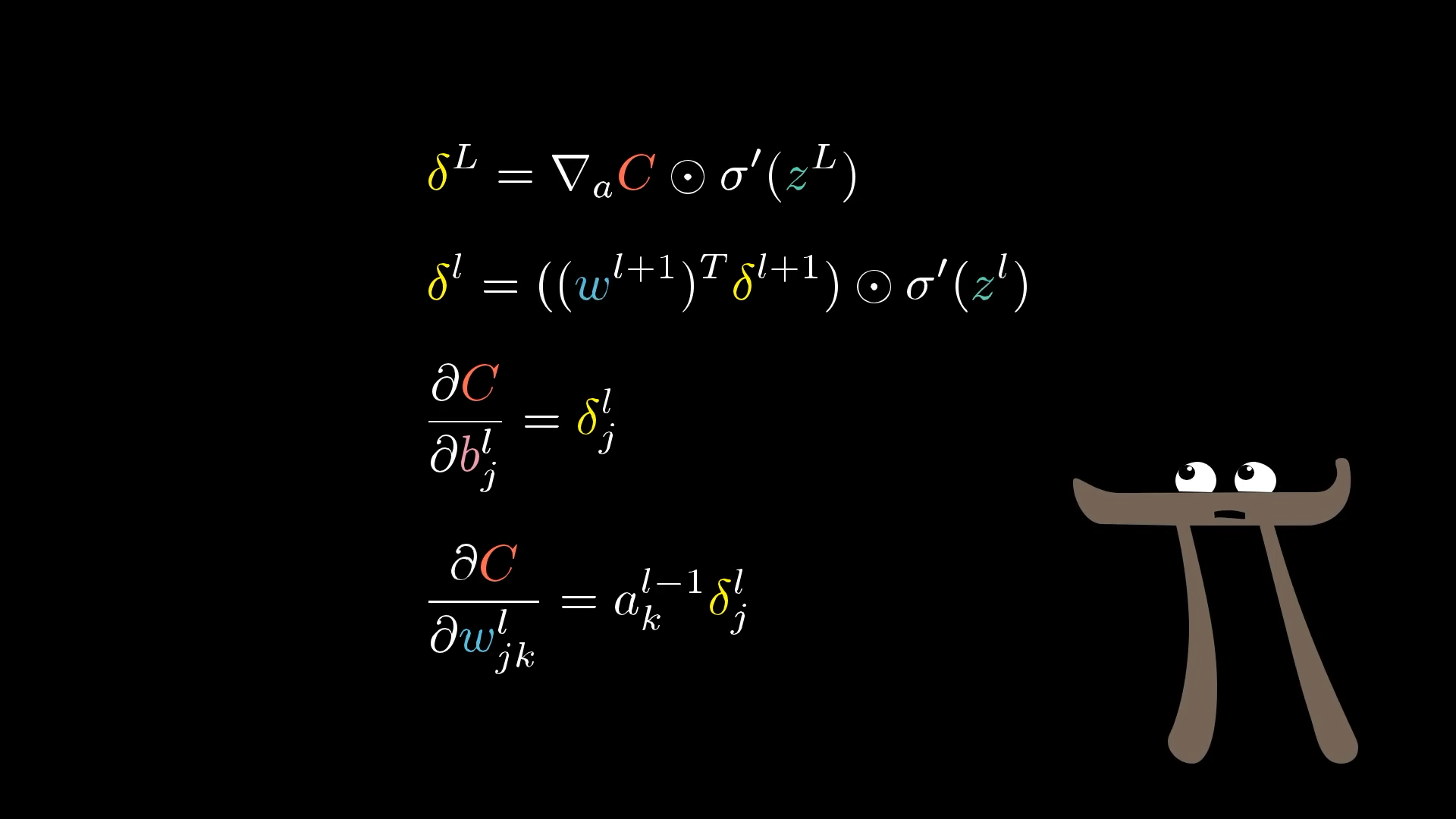
В этой статье давайте начнем с полного игнорирования обозначений и вместо этого рассмотрим влияние каждого обучающего примера на веса и смещения. Надеемся, что эти эффекты будут интуитивно понятны, и к тому времени, когда мы вернемся к нотации, она будет выражать то, что вы уже знаете, а не выступать в качестве кода, который нужно расшифровать.

Поскольку функция полной стоимости предполагает усреднение определенной стоимости за пример для всех десятков тысяч обучающих примеров, способ, которым мы корректируем все веса и смещения для одного шага градиентного спуска, также зависит от каждого отдельного примера. Или, скорее, в принципе так и должно быть, но для повышения эффективности вычислений мы применим небольшую хитрость позже, чтобы избавить вас от необходимости использовать каждый отдельный пример для каждого отдельного шага.

Однако сейчас сосредоточьте свое внимание на одном примере, на этом изображении 2:

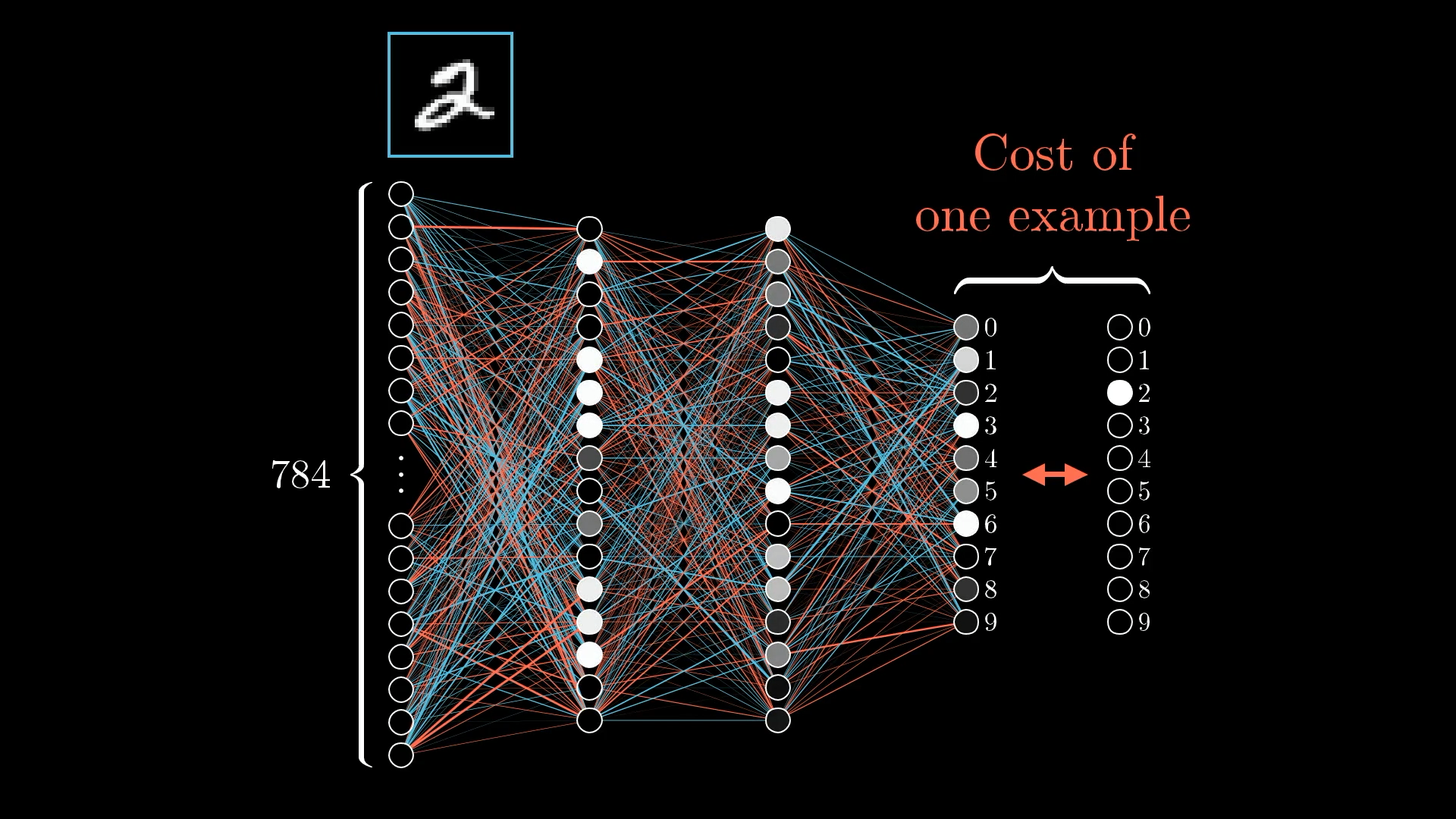
Какой эффект оказывает этот обучающий пример на то, как следует корректировать веса и смещения?

Поскольку сеть еще недостаточно хорошо обучена, активации на этом выходном уровне являются, по сути, случайными. Это не подходит; мы хотим изменить эти активации таким образом, чтобы они правильно идентифицировали цифру 2.

Но помните, что мы можем контролировать только весовые коэффициенты и смещения сети. Поэтому нам придется изменить эти веса и смещения таким образом, чтобы улучшить результат.

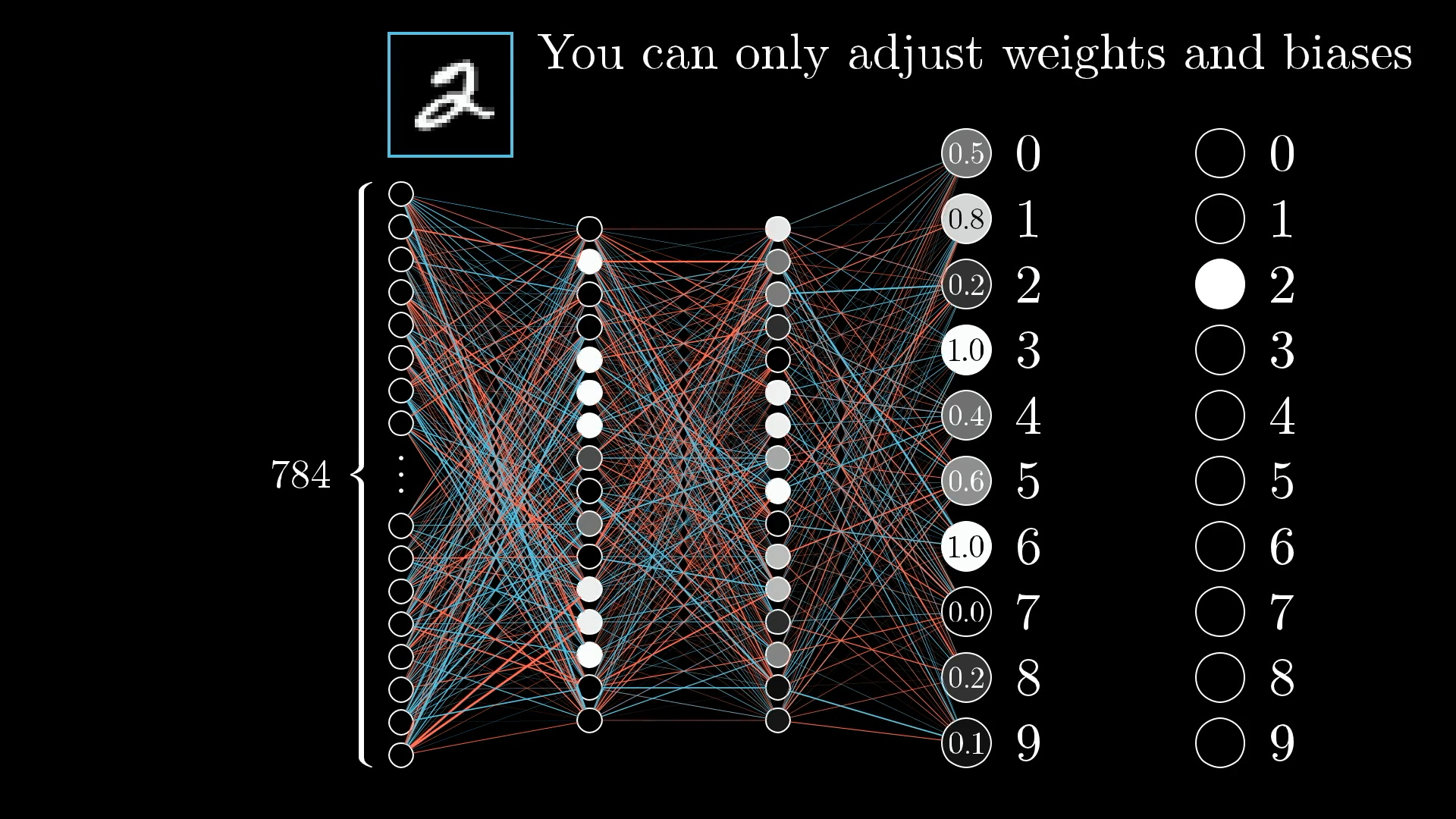
Хотя мы не можем напрямую изменять активации, полезно отслеживать, какие изменения мы хотим внести в этот выходной слой.

Поскольку мы хотим, чтобы сеть классифицировала это как 2, мы хотим, чтобы значение нейрона с цифрой 2 увеличивалось, в то время как все остальные уменьшались:

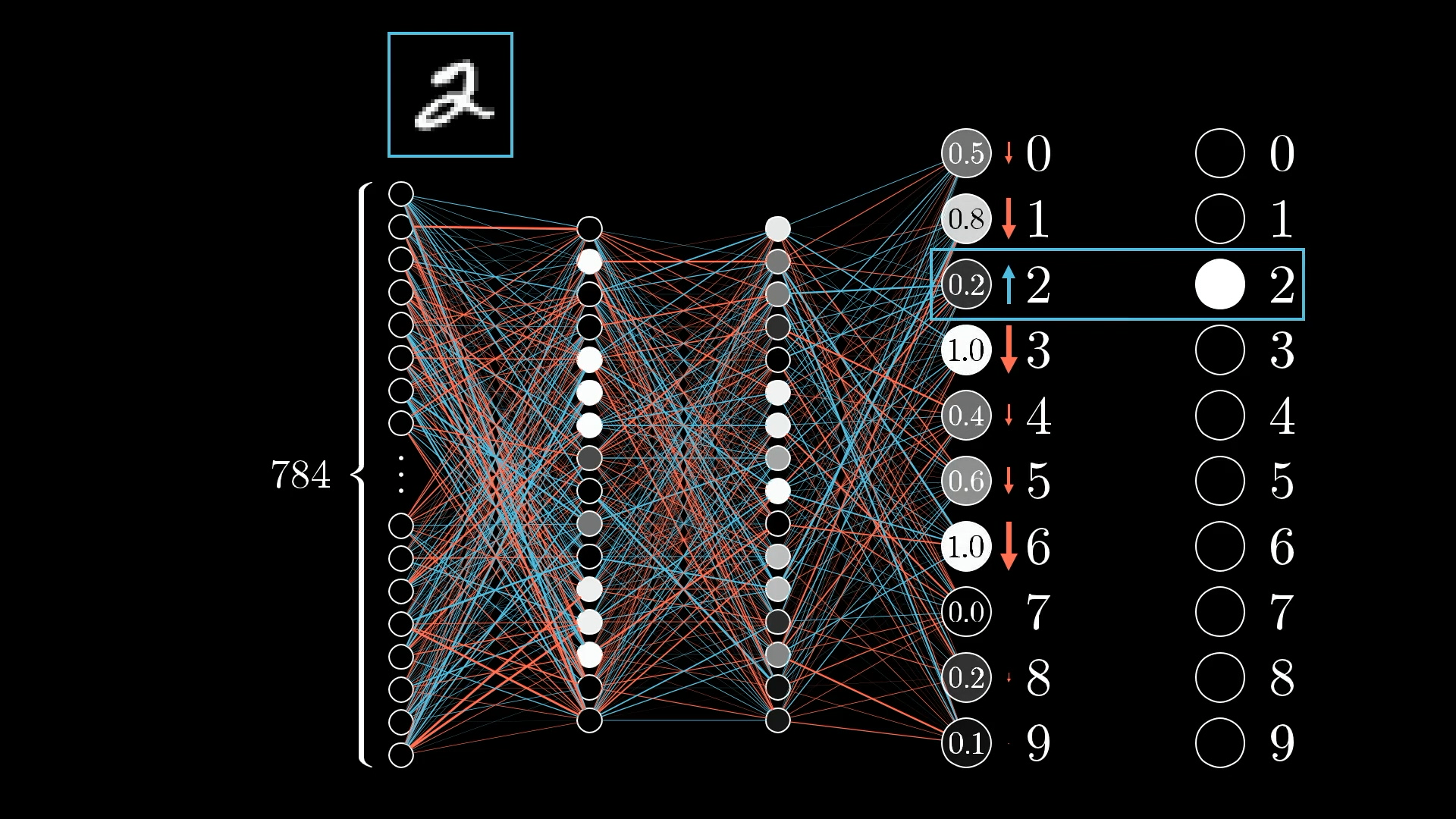
Более того, размеры этих толчков должны быть пропорциональны тому, насколько далеко каждое выходное значение находится от целевого. Нейроны, которые находятся далеко от нормы, требуют сильных толчков, но нейроны, которые довольно близки к правильным, требуют лишь небольших толчков.

Увеличивая масштаб, давайте сосредоточимся на одном нейроне, активацию которого мы хотим увеличить:

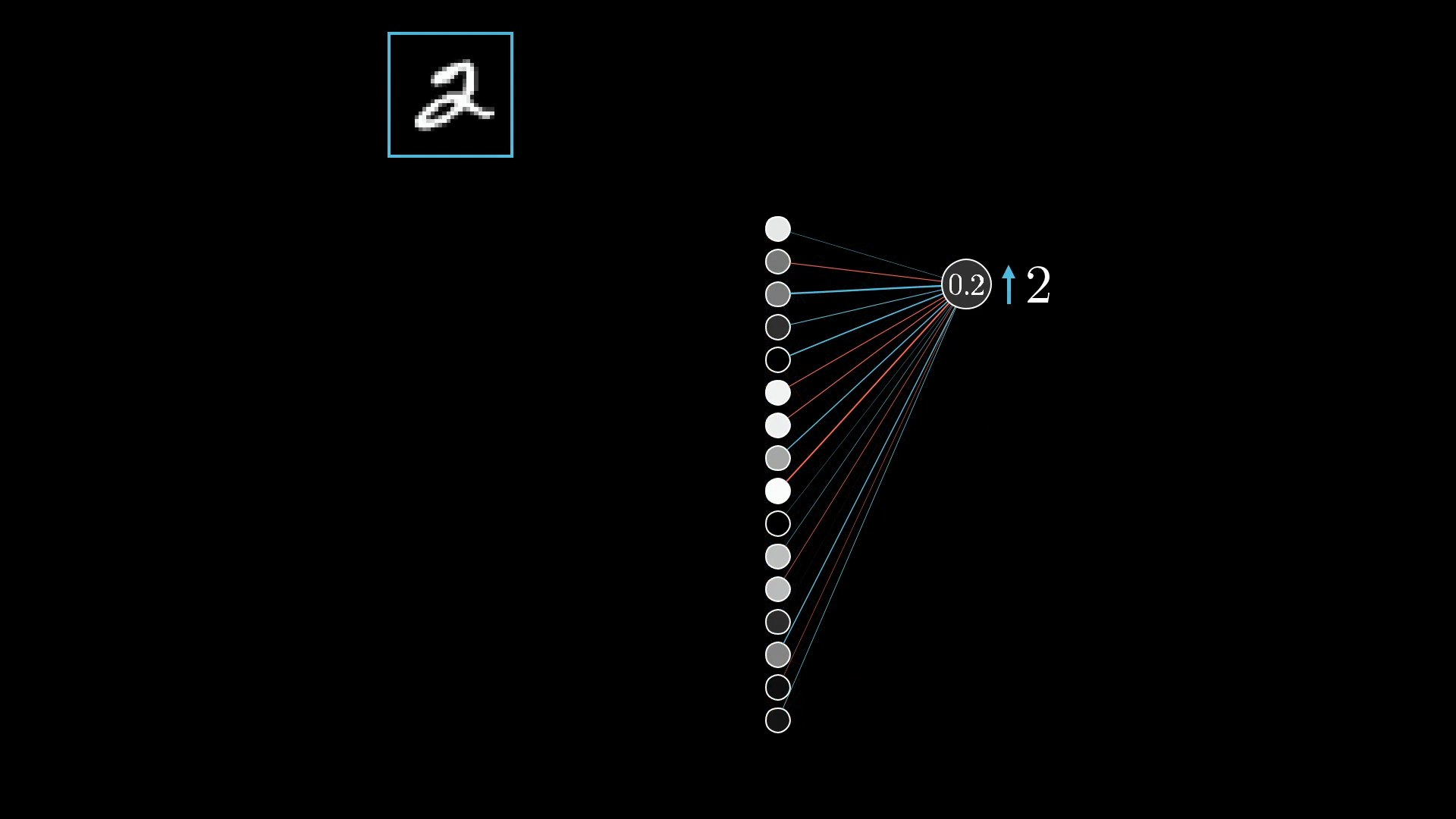
Помните, что его значение активации (в данном случае 0,2) определяется как взвешенная сумма всех активаций предыдущего слоя, плюс смещение, которое затем включается во что-то вроде сигмовидного сжатия или ReLU:

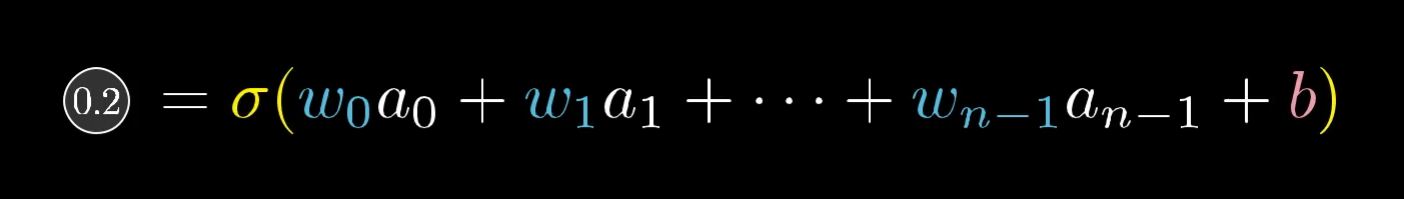
Таким образом, есть три способа, которые можно объединить, чтобы увеличить эту активацию:

• Увеличить смещение
• Увеличить веса
• Изменить активации с предыдущего уровня

Изменение смещения

Изменение смещения, связанного с нейроном, - это самый простой способ изменить его активацию. В отличие от изменения весов или активаций предыдущего уровня, влияние изменения смещения на взвешенную сумму является постоянным и предсказуемым.

Смещение, связанное с разрядным нейроном 2, должно быть увеличено, потому что это приведет к увеличению активации разрядного нейрона 2. Все остальные выходные активации должны быть уменьшены, что требует уменьшения связанных с ними смещений.

Эти изменения позволят получить более точный прогноз при меньших затратах для данного конкретного примера обучения.

Изменение значений весов

Как следует настроить значения весов? Обратите внимание, что, поскольку они умножаются на количество активаций, значения весов имеют разные уровни влияния:

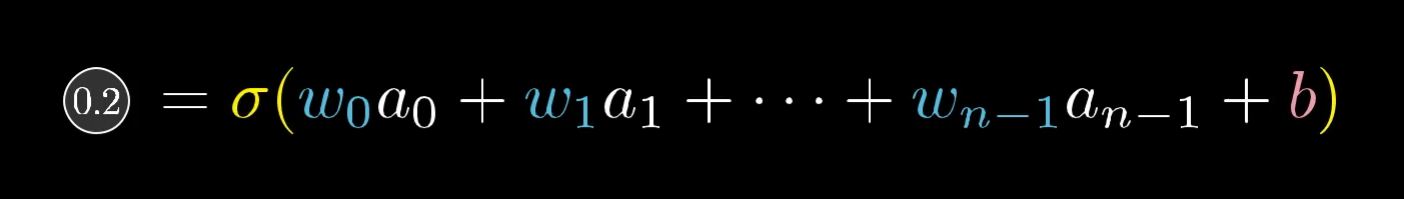
Изменение значений, связанных с большими значениями активации, будет иметь более сильный эффект, чем изменение значений, связанных с малыми значениями активации.

Связи с самыми яркими нейронами из предыдущего слоя имеют наибольший эффект, поскольку их весовые коэффициенты умножаются на большее значение активации. Таким образом, увеличение одного из этих весов оказывает большее влияние на функцию стоимости, чем увеличение веса связи с более тусклым нейроном. (Опять же, все это относится только к одному учебному примеру.)

Помните, что когда мы говорим о градиентном спуске, нас волнует не только то, следует ли перемещать каждый компонент вверх или вниз. Мы заботимся о том, какие из них дают вам наибольшую отдачу.

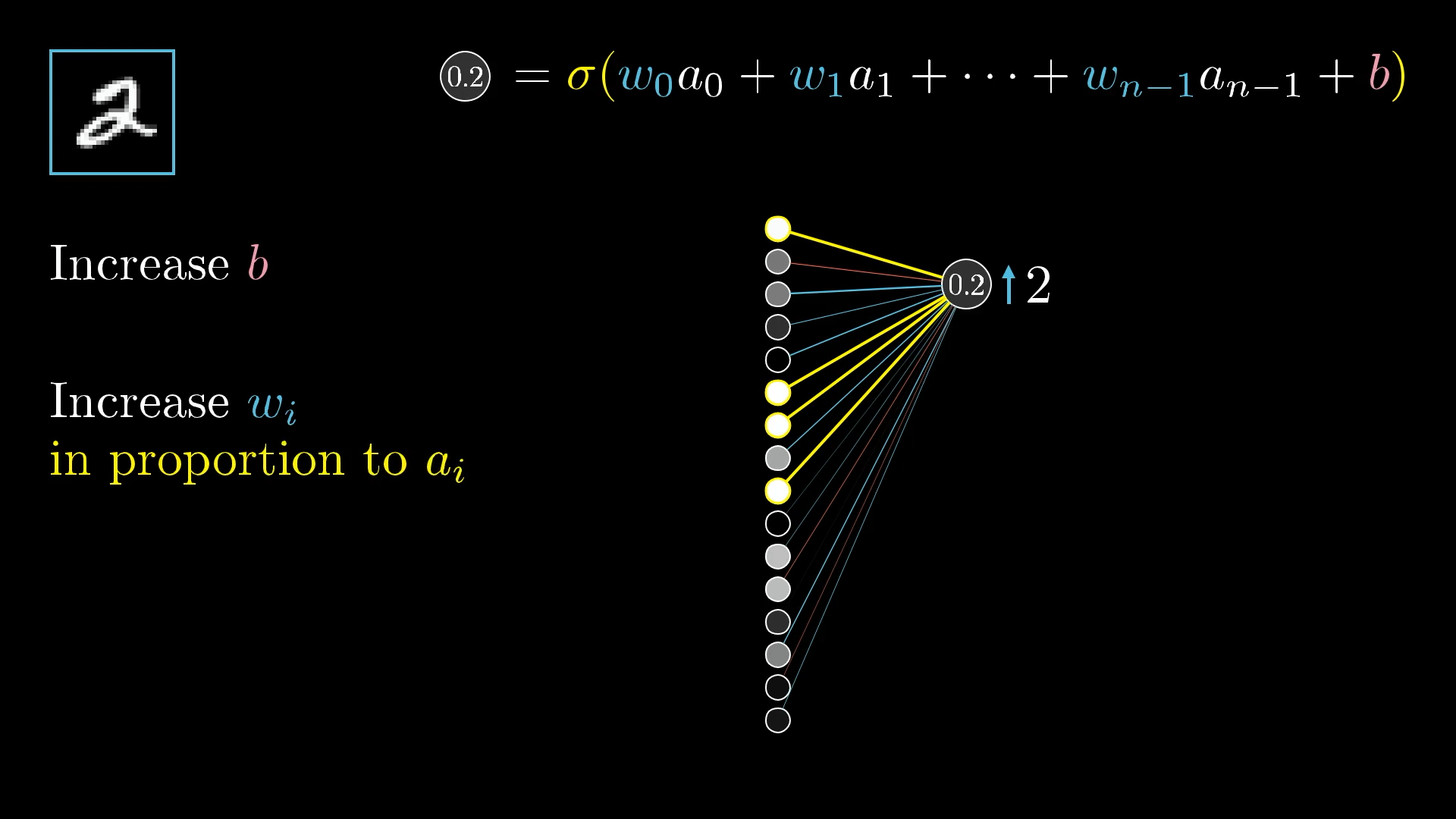
Это, кстати, по крайней мере в некоторой степени напоминает теорию нейробиологии о том, как обучаются биологические сети нейронов, теорию Хебба, которую часто обобщают фразой “нейроны, которые запускаются совместно, соединяются проводами”. Здесь наибольшее увеличение веса — самое сильное укрепление связей — происходит между нейронами, которые являются наиболее активными, и теми, которые мы хотели бы активизировать.

В некотором смысле, нейроны, которые активируются при виде цифры 2, становятся более тесно связанными с теми, которые активируются при мысли о цифре 2.

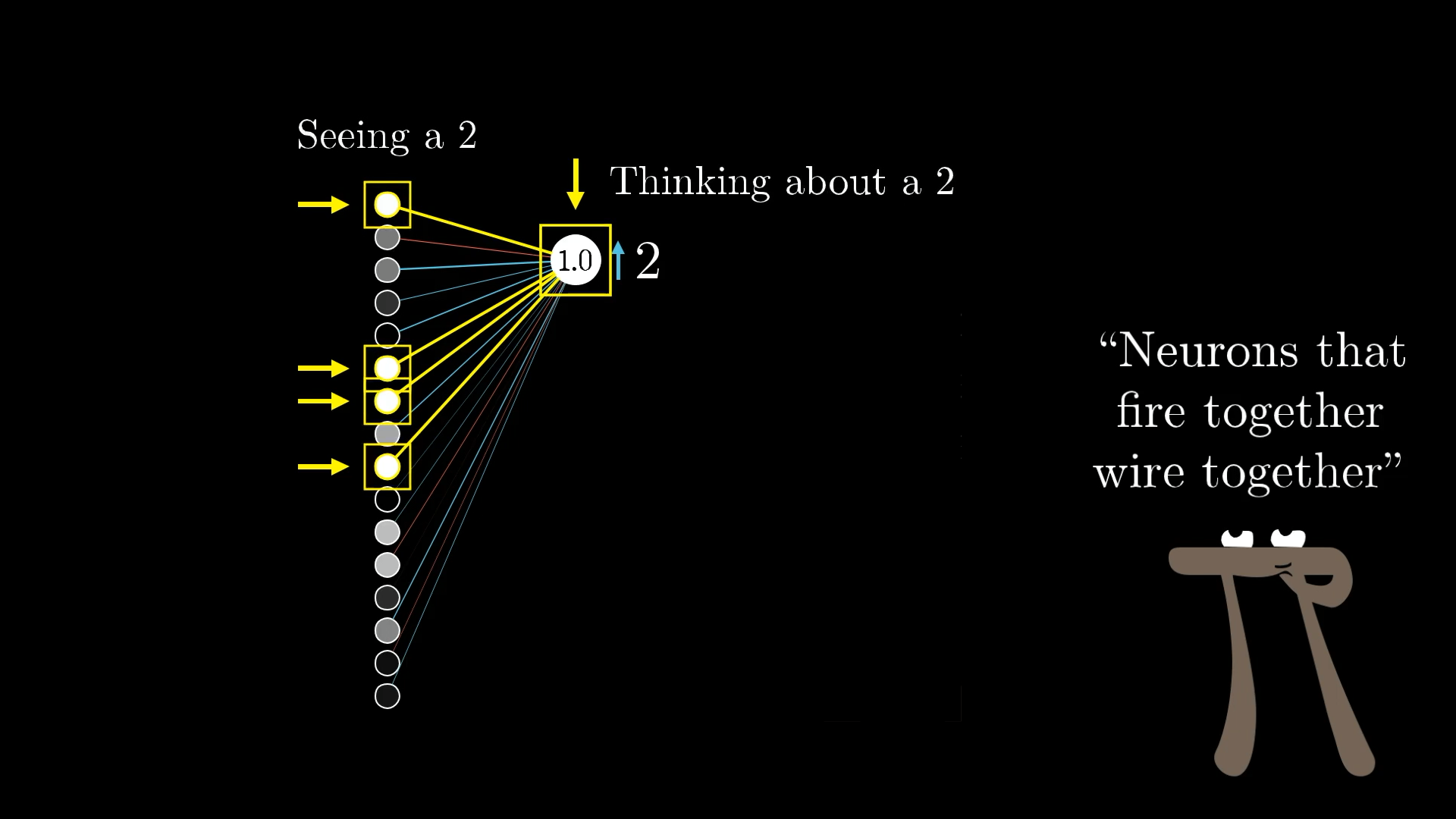
Аналогия не идеальна, поскольку неподготовленная сеть на самом деле не “думает” о цифре 2, когда видит этот пример; скорее, метка на обучающих данных жестко определяет, о чем должна думать сеть. Тем не менее, приятно осознавать, что скрытые под всем этим математическим анализом и линейной алгеброй, обычно используемыми для описания обратного распространения, фактические изменения, происходящие с весами в каждом обучающем примере, отражают идеи теории Хебба.

Изменение активаций

Третий способ, которым мы можем повысить активацию этого нейрона, - это изменить все активации на предыдущем уровне. А именно, если бы все, что связано с этим нейроном цифры 2 с положительным весом, было ярче, а если бы все, что связано с отрицательным весом, было тусклее, этот нейрон цифры 2 был бы более активным.

Как и в случае с изменением веса, вы получите максимальную отдачу от своих усилий, добиваясь изменений, пропорциональных размеру соответствующих весов:

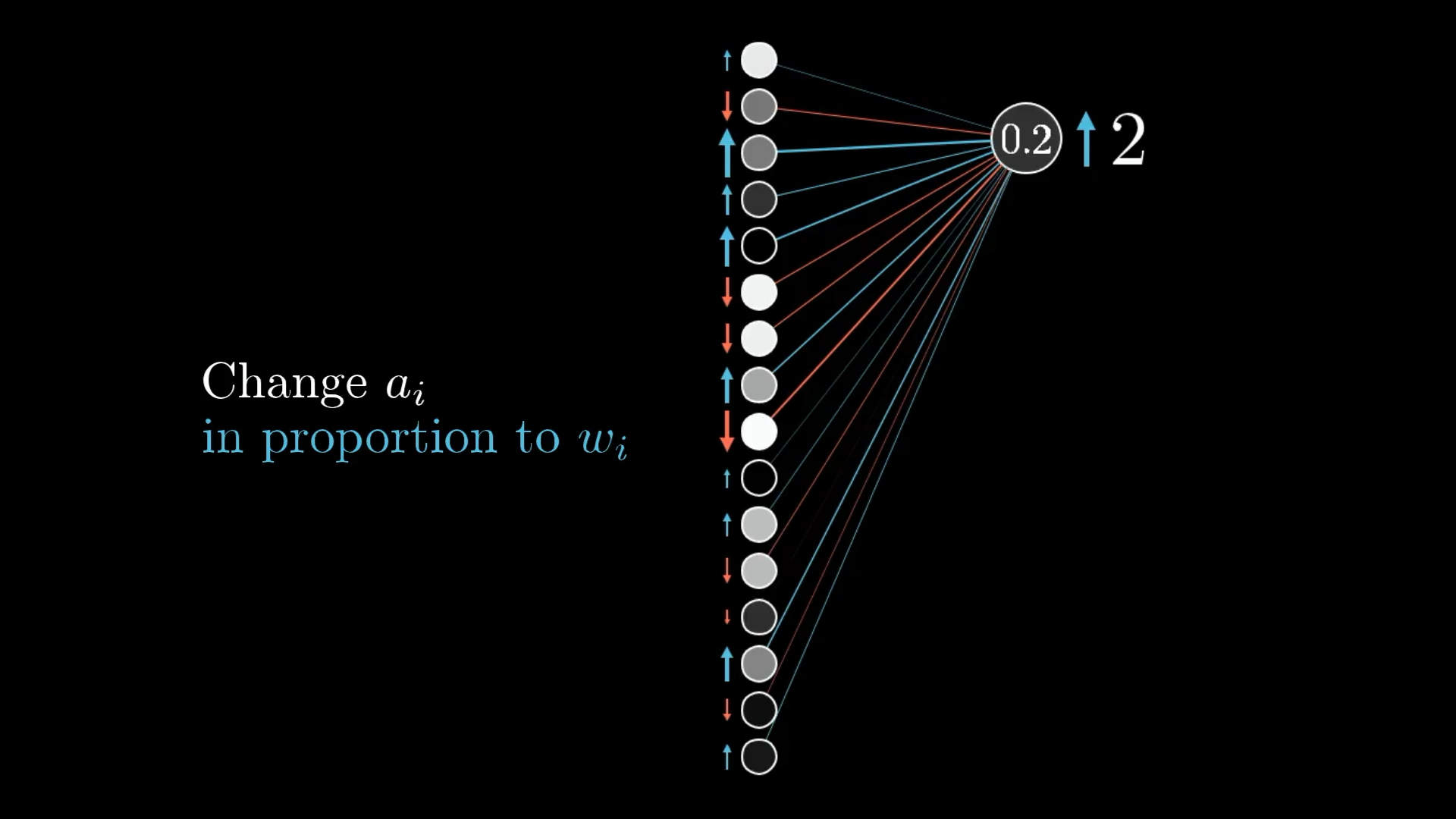
Точно так же, как при изменении веса пропорционально активациям, вы получаете максимальную отдачу от вложенных средств, увеличивая количество активаций пропорционально связанному с ними весу.

Конечно, мы не можем напрямую влиять на эти активации. Мы можем контролировать только веса и отклонения. Но, как и в случае с предыдущим слоем, полезно помнить о желаемых изменениях.

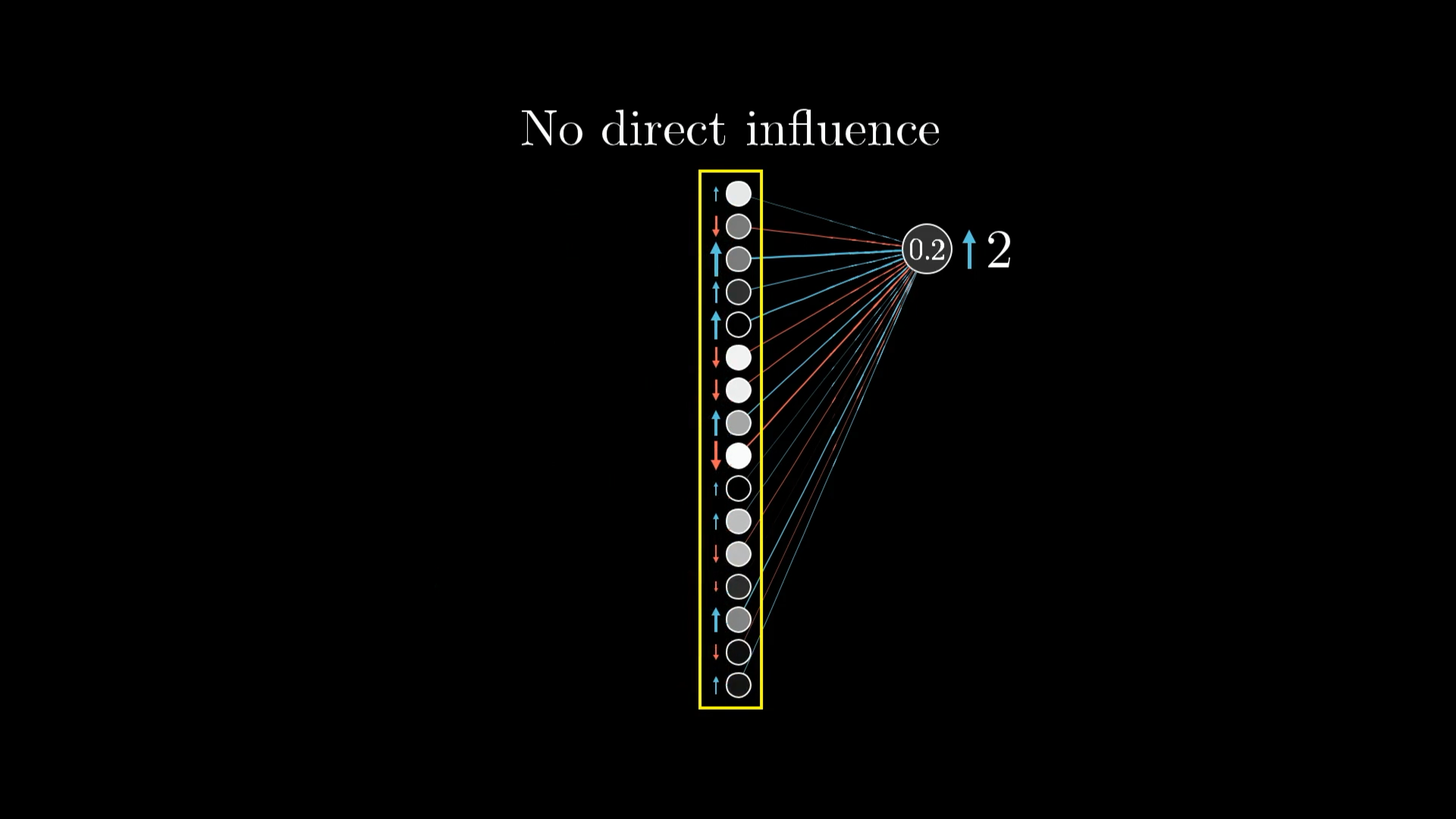
Мы не можем напрямую влиять на активации в предыдущем слое. Но мы можем изменять веса и смещения, которые определяют их значения!

Помните, что этого хочет только один выходной нейрон с цифрой 2. Мы также хотим, чтобы все остальные нейроны в последнем слое стали менее активными, и каждый из этих выходных нейронов по-своему влияет на то, что должно произойти с предпоследним слоем.

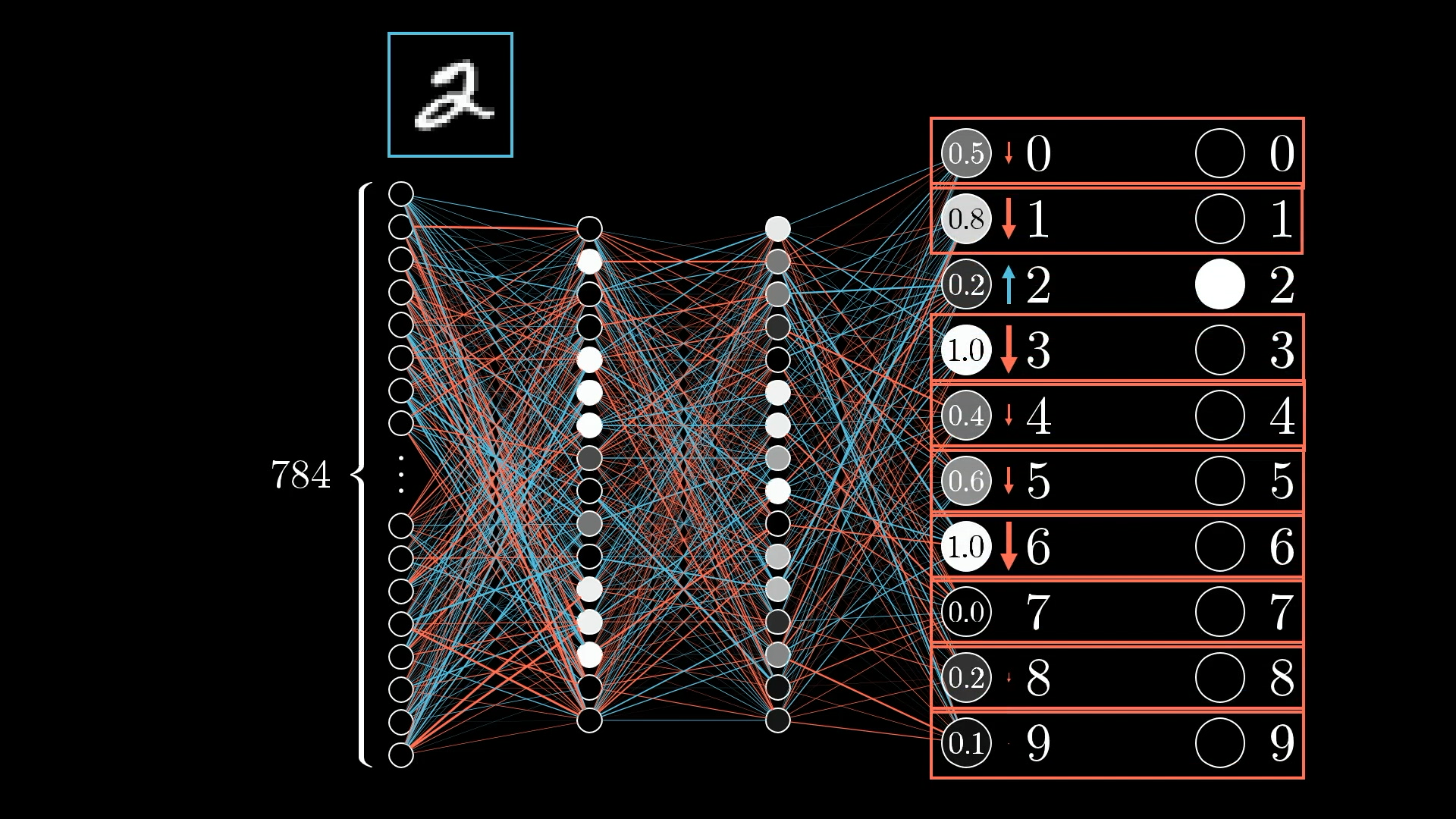
Мы хотим настроить и все остальные выходные нейроны, что означает, что у нас будет много конкурирующих запросов на изменение активаций на предыдущем уровне.

Таким образом, желание этого нейрона с цифрой 2 суммируется с желаниями всех остальных девяти нейронов. У каждого из них есть свой собственный предполагаемый толчок для этого предпоследнего слоя, опять же пропорционально соответствующим весам и пропорционально тому, насколько каждый нейрон должен измениться.

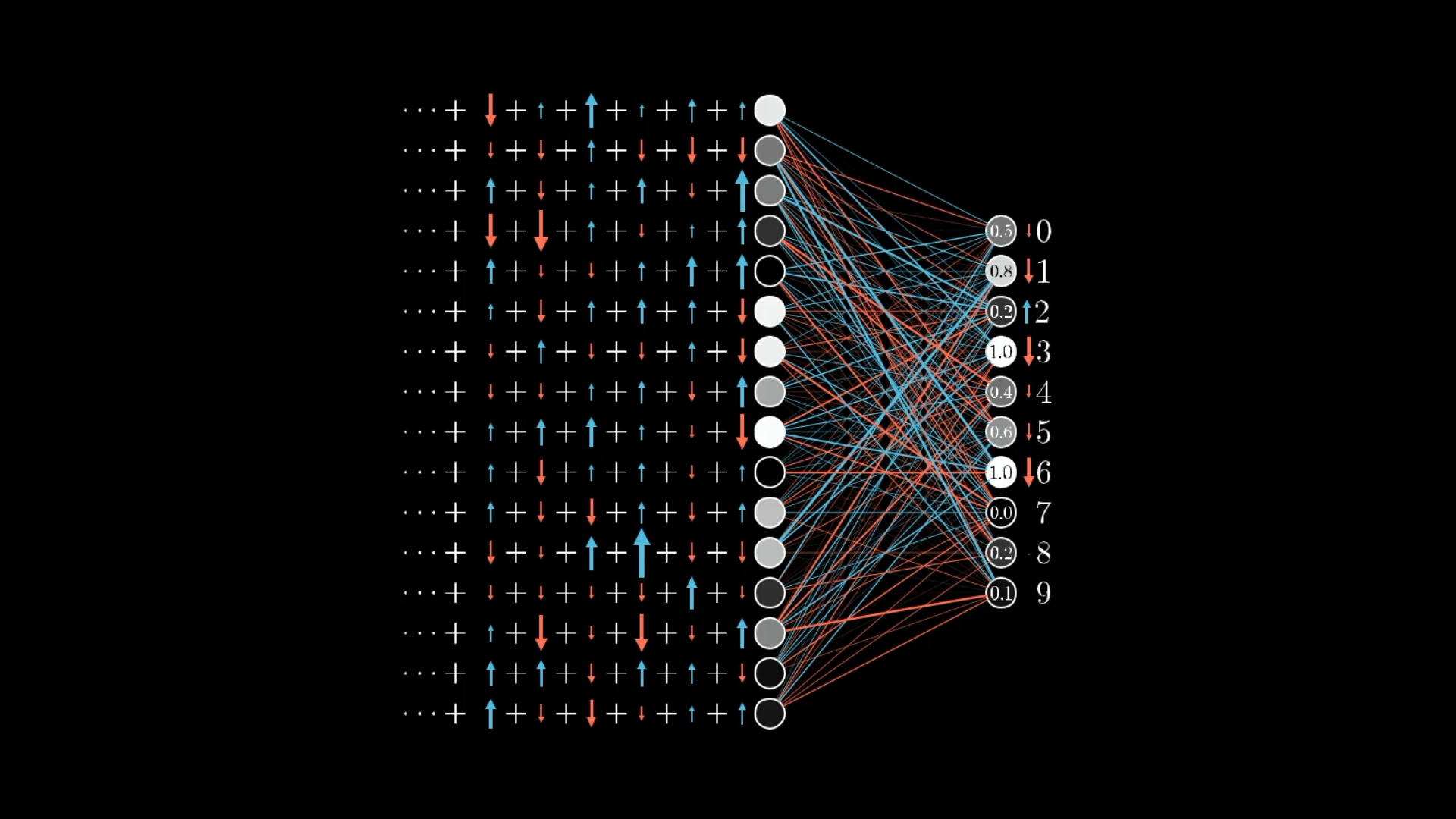
Невозможно полностью удовлетворить все эти конкурирующие требования к активациям на втором уровне. Лучшее, что мы можем сделать, - это сложить все желаемые изменения, чтобы получить общее желаемое изменение.

Вот тут-то и возникает идея обратного распространения. Добавив все эти желаемые эффекты, вы можете получить список изменений, которые вы хотите внести в предпоследний слой. После этого вы можете рекурсивно применить тот же процесс к соответствующим весам и смещениям, определяющим эти значения, повторяя этот процесс при перемещении в обратном направлении по сети.

Повторяем для всех обучающих примеров

Все, с чем мы только что ознакомились, отражает только то, как один обучающий пример может повлиять на каждый из множества весов и смещений.

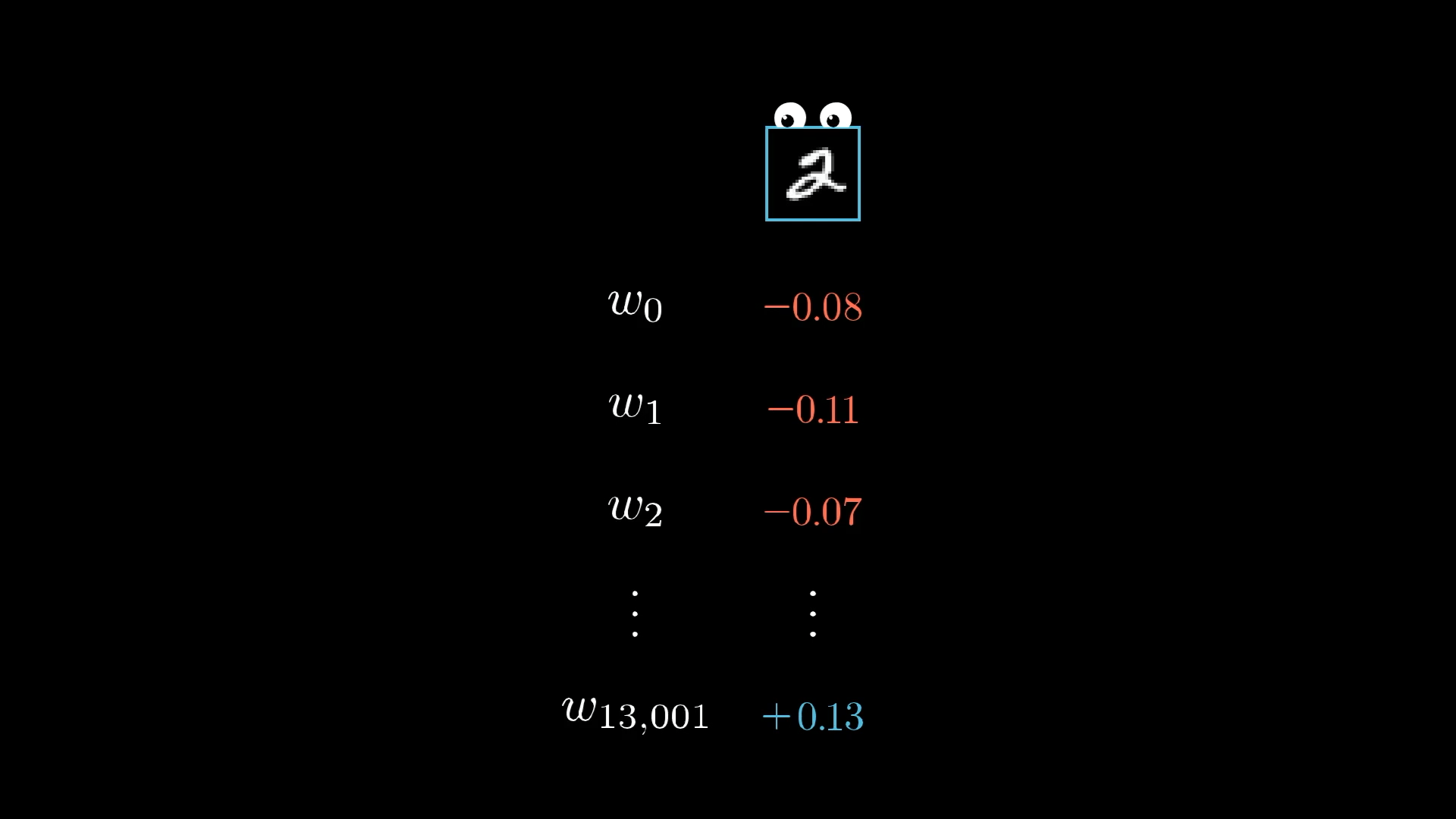
Пока что мы определили только те изменения в весах и смещениях, которые улучшили бы наши результаты для цифры 2. Но нам также нужно учитывать все остальные цифры!

Если бы мы только прислушались к тому, чего хочет изображение с цифрой 2, у сети в конечном итоге появился бы стимул просто классифицировать все изображения как 2.

Чтобы немного уменьшить масштаб, вы также выполняете ту же процедуру обратного распространения для каждого другого тренировочного примера, записывая, как каждый из них хотел бы изменить веса и смещения. Затем вы усредняете все эти желаемые изменения.

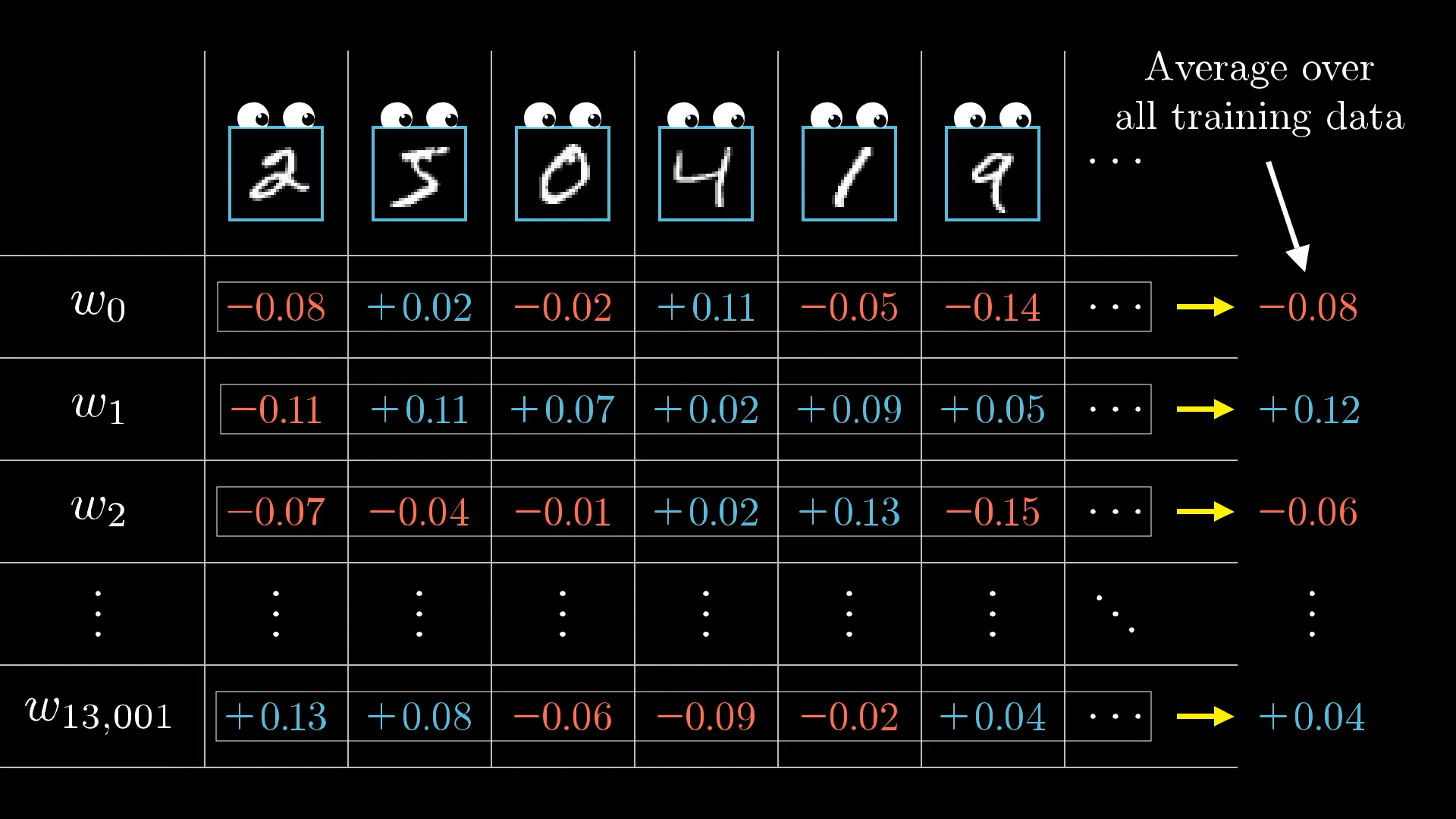
В каждом обучающем примере есть свои требования к тому, как следует корректировать веса и смещения и с какой относительной силой. Усредняя требования всех обучающих примеров, мы получаем конечный результат, показывающий, как следует изменить данный вес или смещение за один шаг градиентного спуска.

Совокупность этих усредненных значений для каждого веса и смещения, грубо говоря, является отрицательным градиентом функции затрат! Или, по крайней мере, чем-то пропорциональным ему.

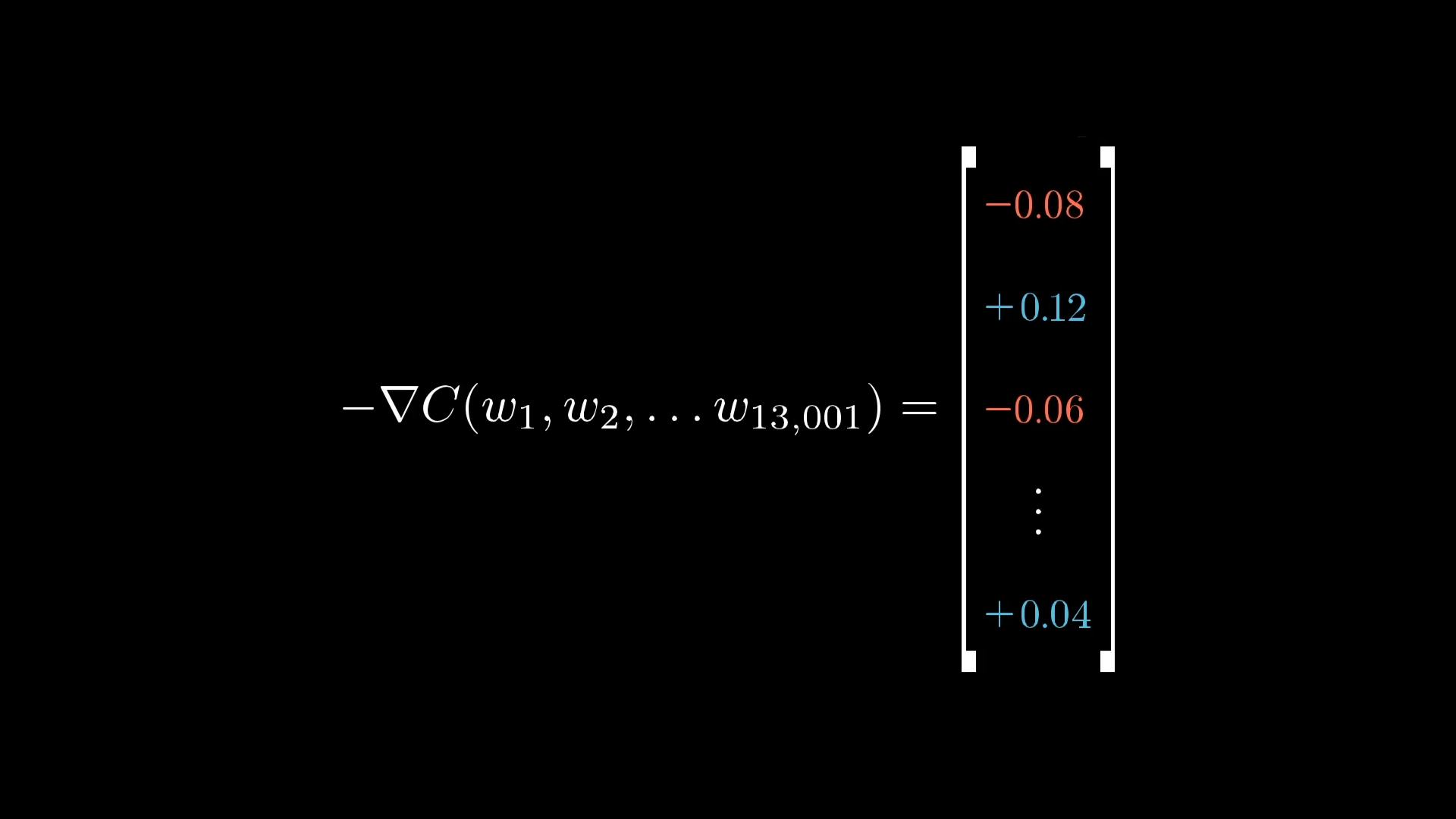
Результатом всего этого обратного распространения является то, что мы нашли (что-то пропорциональное) отрицательному градиенту!

Я говорю “грубо говоря” только потому, что мне еще предстоит получить количественную оценку этих толчков. Но если вы поняли каждое изменение, на которое я ссылался выше, почему некоторые из них пропорционально больше, чем другие, и как все они должны быть объединены, тогда вы понимаете механику того, что на самом деле делает обратное распространение.

Стохастический градиентный спуск

На практике компьютерам требуется чрезвычайно много времени, чтобы суммировать влияние каждого отдельного обучающего примера на каждый отдельный шаг градиентного спуска. Вместо этого существует хитроумный способ ускорить процесс, который включает в себя большее количество этапов градиентного спуска, но гораздо меньшее время на каждый из них.

Случайным образом перемешайте ваши обучающие данные и разделите их на несколько мини-пакетов, содержащих, скажем, по 100 обучающих примеров в каждом.

Затем вы вычисляете шаг градиентного спуска в соответствии с каждым мини-пакетом, а не со всем набором обучающих примеров. Это не даст вам фактического градиента функции затрат, который зависит от всех обучающих данных, поэтому это не самый эффективный шаг на спуске. Но каждая мини-партия дает довольно хорошее приближение, и если имеется 100 мини-партий, то каждый шаг занимает 1/100 от общего времени. И после 100 шагов каждая часть обучающих данных будет иметь возможность повлиять на конечный результат.

С этими мини-сериями, которые лишь приблизительно соответствуют градиенту, процесс спуска по градиенту больше похож на то, как пьяный человек бесцельно спускается с холма, но делает быстрые шаги, а не на тщательно рассчитанного человека, который делает медленные, обдуманные шаги вниз по склону.

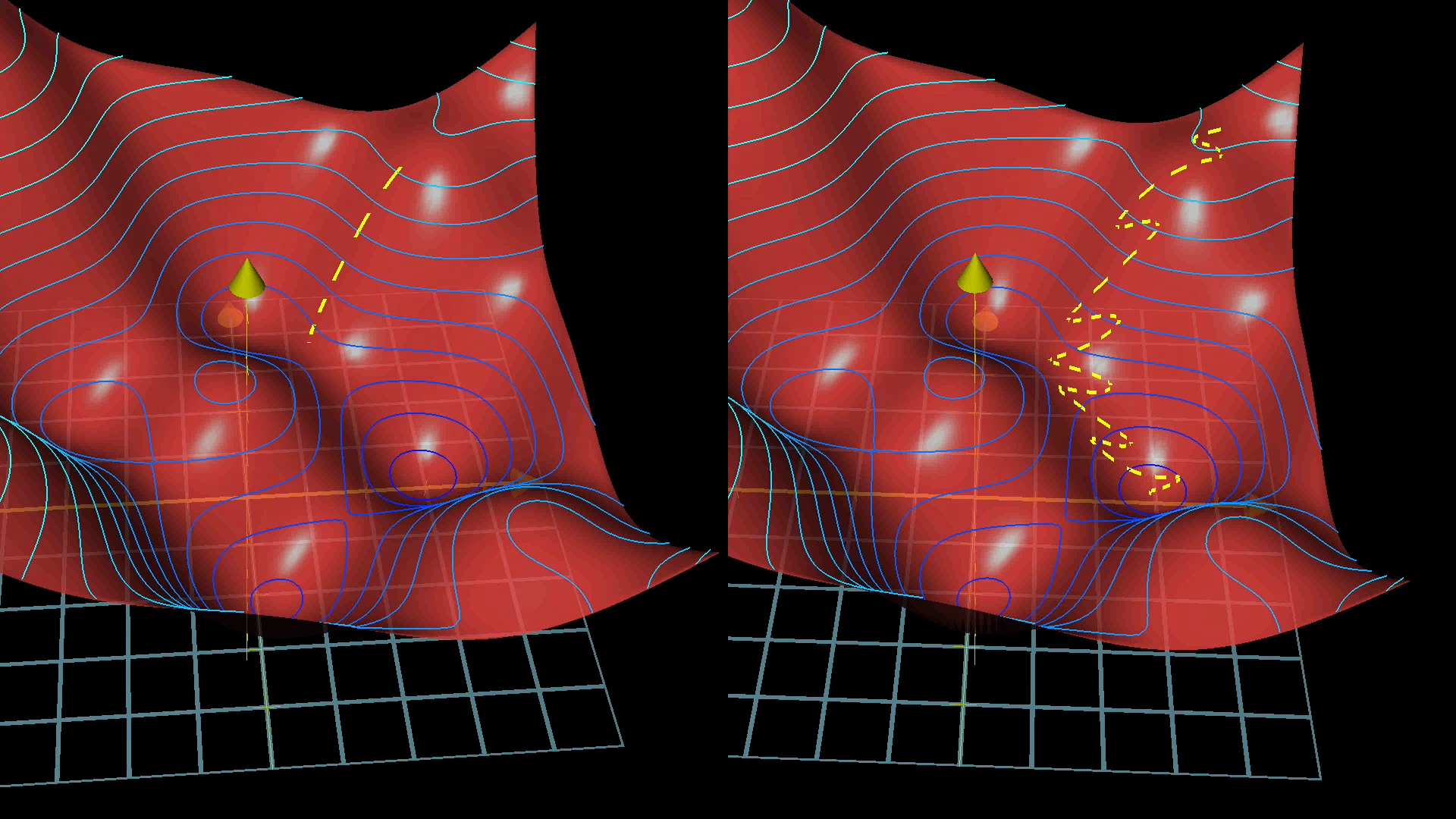
Использование мини-пакетов означает, что наши шаги на спуске не такие точные, но они выполняются намного быстрее.

Это называется стохастическим градиентным спуском.

Формализация алгоритма обратного распространения ошибки

Алгоритм обучения сводится к немного модифицированному градиентному спуску. В данном примере мы будем вычислять ошибку для каждого объекта обучающей выборки. Для градиентного спуска нам нужно сформировать функцию ошибки. Возьмем среднеквадратическое отклонение. В данном случае, так как используется всего один объект, это будет просто квадрат отклонения эмпирического значения от полученного:

\[С_0 = (a^{(L)} - y)^2\]

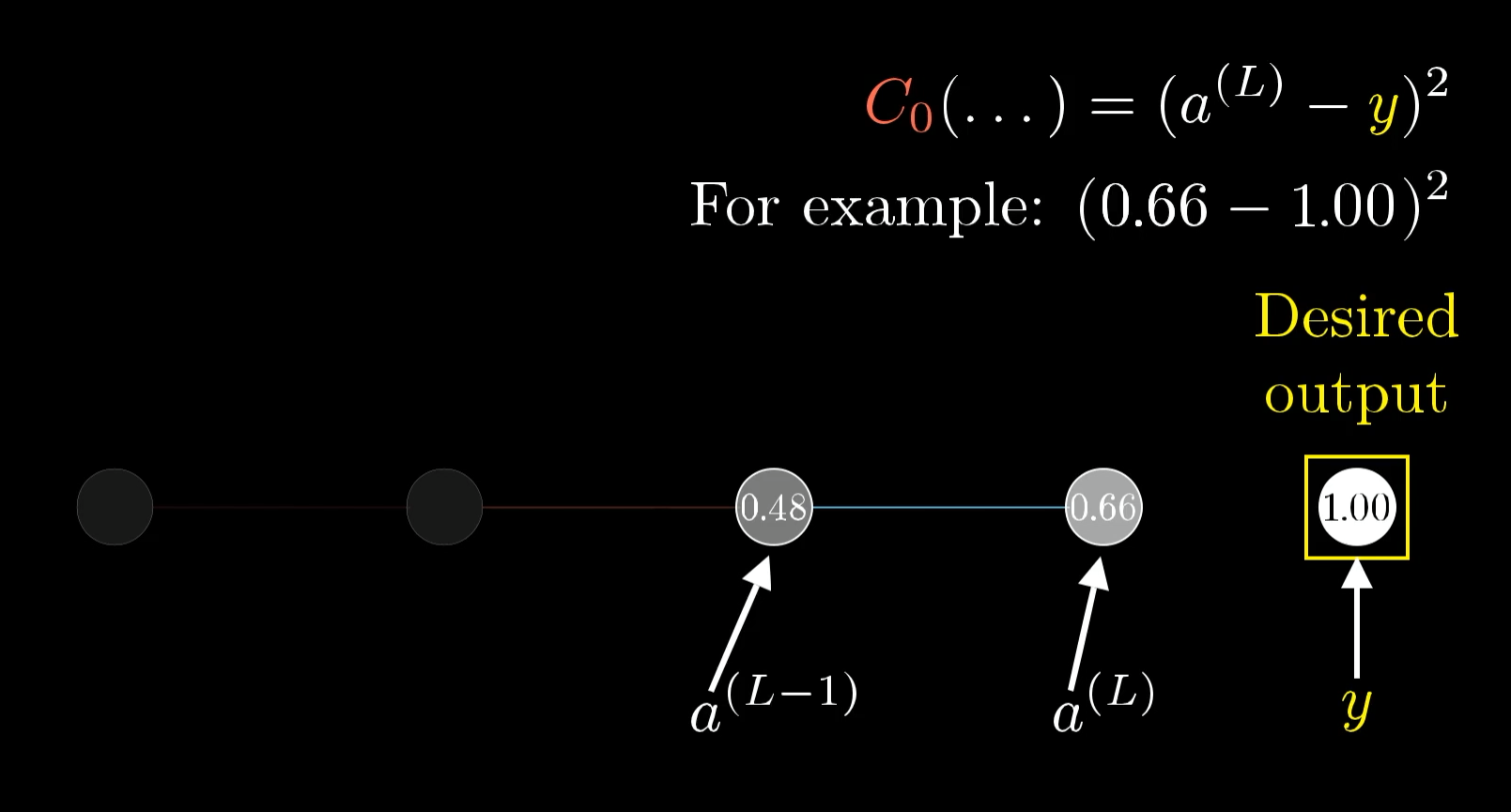
В этой формуле $y$ - эмпирическое или истинное значение целевой функции. А $a^{(L)}$ - это значение функции активации нейрона на последнем слое. Другими словами это по сути и есть значение модели. В нейронных сетях так принято обозначать результат работы нейрона, и эти обозначения станут полезными, когда мы будем говорить о многослойных сетях. $L$ в данном случае - просто количество слоев.

При описании математики работы нейронных сетей часто приходится видеть обозначение номера слоя в виде верхнего индекса в скобках. Следует помнить, что это не возведение в степень, а именно индекс, то есть просто номер слоя, которому принадлежит данный параметр. Дело в том, что нижние индексы обычно заняты обозначением номера нейрона в слое. Также обратите внимание, что к слоям мы обращаемся с конца - сначала работаем с последним, затем с предпоследним и так далее. Это же алгоритм обратного распространения ошибки. Поэтому мы обозначаем слои не 1, 2, …, а через $L$ - количество слоев - $L$ - последний, $L-1$ - предпоследний и так далее.

Результат работы нейрона зависит от трех факторов - от значения весов $w^{(L)}_i$ (опять в обозначениях упоминается номер слоя, в данном случае - последний), от значений функции активации нейронов предыдущего слоя и от свободного парамера $b^{(L)}$.

\[a^{(L)} = \sigma ( w^{(L)} a^{(L-1)} + b^{(L)} )\]

\[z^{(L)} = w^{(L)} a^{(L-1)} + b^{(L)}\] \[a^{(L)} = \sigma ( z^{(L)} )\]

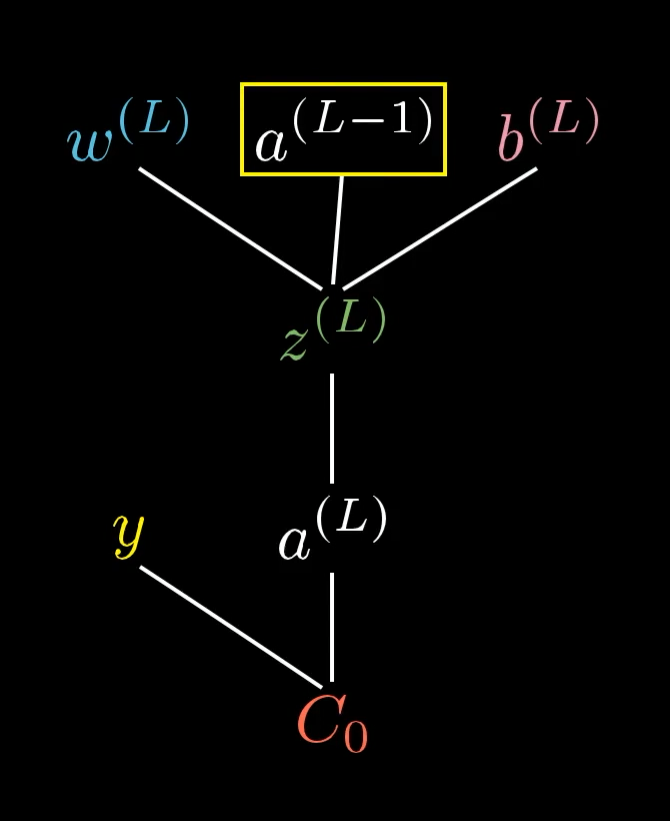
Вы могли бы представить это так: вес, предыдущая активация и смещение вместе позволяют нам вычислить $z^{(L)}$, что, в свою очередь, позволяет нам вычислить $a^{(L))$ что, в свою очередь, вместе с константой y позволяет нам вычислить стоимость $C_0$.

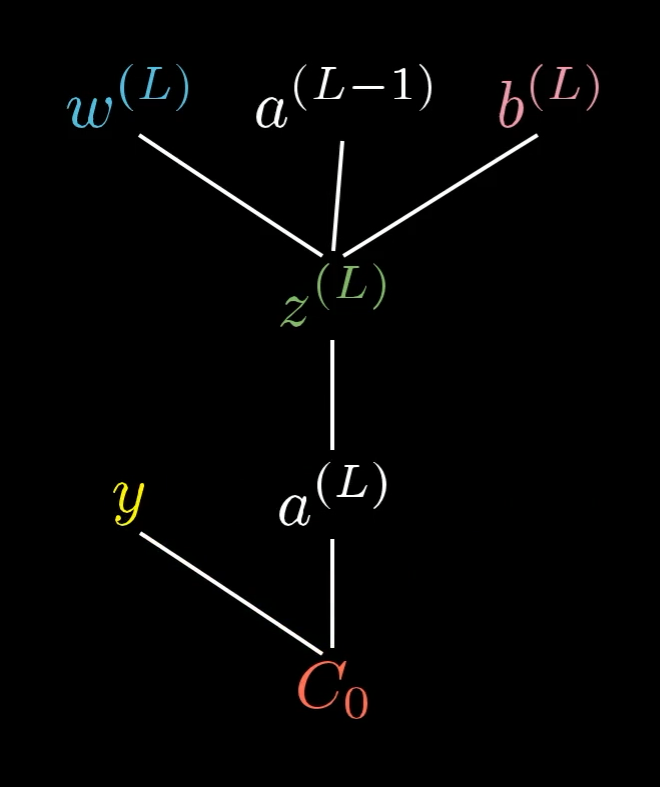
И, конечно, на $a^{(L−1)}$ влияют его собственный вес и bias, что означает, что наше дерево на самом деле простирается выше…

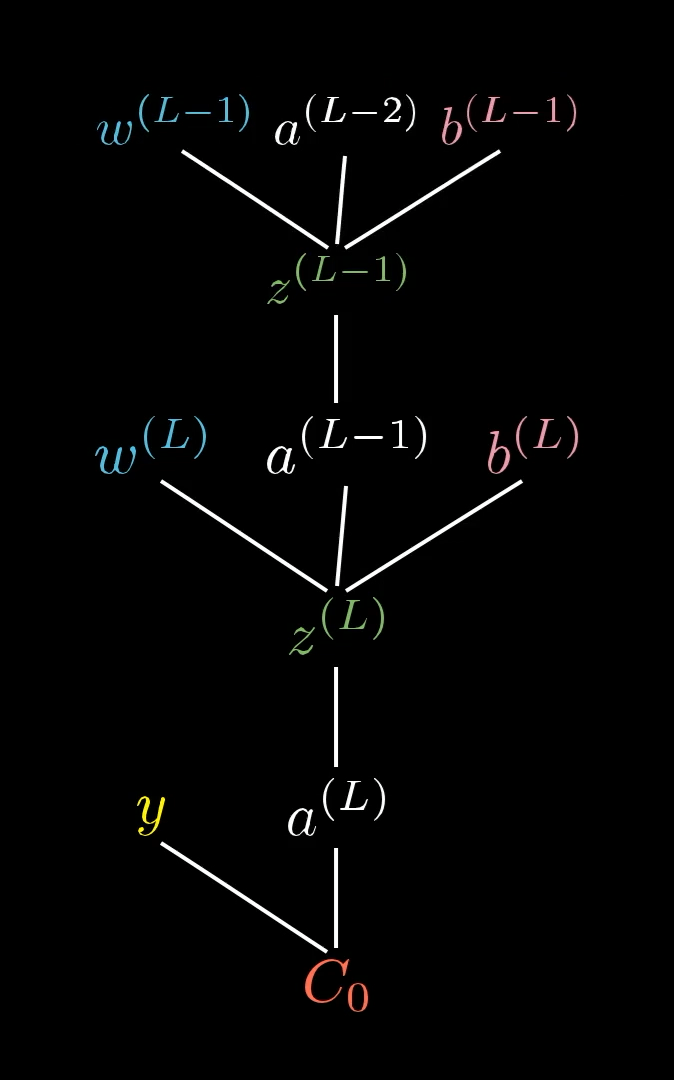
Вычисление производной по весам последнего слоя

Нам нужно понять, как на ошибку $C_0$ влияют изменения весов последнего слоя нейросети $w^{(L)}$. То есть нам нужно вычислить производную $\frac{\partial C_0}{\partial w^{(L)}}$.

Когда вы увидите этот термин ∂w(L), подумайте о нем как о “некотором незначительном увеличении w(L)”, например, изменении на 0,01. И подумайте о том, что этот термин ∂C0 означает “каким бы ни было результирующее увеличение затрат”. Нам нужно их соотношение.

Концептуально, этот незначительный сдвиг в сторону w(L) вызывает некоторый сдвиг в сторону z(L), который, в свою очередь, вызывает некоторое изменение в a(L), что напрямую влияет на стоимость, C0.

Итак, мы разберем это, сначала взяв отношение небольшого изменения z(L) к незначительному изменению w(L). То есть производную z(L) по отношению к w(L). Аналогично, рассмотрим отношение незначительного изменения a(L) к вызвавшему его незначительному изменению z(L), а также соотношение между конечным значением C0 и этим промежуточным значением a(L).

\[\frac{\partial C}{\partial w^{(L)}} = \frac{\partial C}{\partial a^{(L)}} \cdot \frac{\partial a^{(L)}}{\partial z^{(L)}} \cdot \frac{\partial z^{(L)}}{\partial w^{(L)}}\]

Другими словами, зависимость значения ошибки от веса складывается из зависимости значения ошибки от значения нейрона, зависимость значения нейрона от линейной комбинации и значения линейной комбинации от веса. Давайте найдем эти частные производные по порядку:

\[C_0 = ( a^{(L)} - y )^2\] \[\frac{\partial C_0}{\partial a^{(L)}} = 2(a^{(L)} - y)\]

Зависимость ошибки от значения нейрона следует из самой формулировки функции ошибки. Заметим только, что постоянный множитель можно в дальнейшем игнорировать, так как по методу градиентного спуска мы все равно будем домножать получившееся выражение на скорость обучения. Она пропорциональна разнице между фактическим результатом и желаемым результатом. Это означает, что когда фактический результат значительно отличается от того, что мы хотим, даже небольшие изменения в режиме активации могут существенно повлиять на ошибку.

При расчете частной производной значения функции активации нейрона от линейной комбинации мы сталкиваемся с проблемой. Дело в том, что мы используем ступенчатую функцию активации, а ее производная равна нулю везде, где определена. По этой самой причине эта функция активации и не используется в многослойных нейронных сетях. Сейчас, без потери обучающей способности метода мы примем эту производную за единицу. Но имейте в виду, что в общем случае так делать нельзя, это математический трюк только для однослойного перцептрона и только для этой функции активации.

\[\frac{\partial a^{(L)}}{\partial z^{(L)}} = 1\]

В общем же случае:

\[a^{(L)} = \sigma ( z^{(L)} )\] \[\frac{\partial a^{(L)}}{\partial z^{(L)}} = \sigma ' ( z^{(L)} )\]

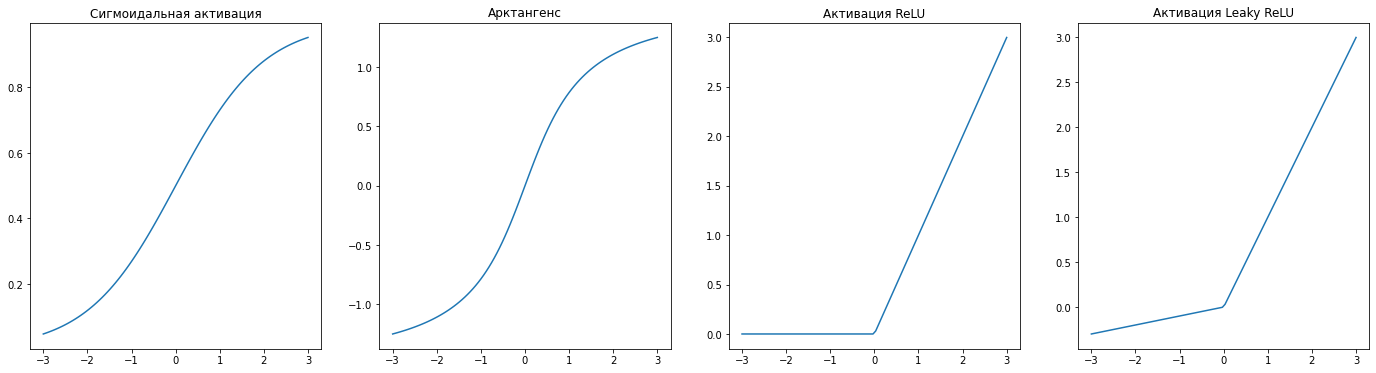
Частная производная линейной комбинации по весу равна входному значению. В данном случае - это сами атрибуты датасета, которые подаются на вход нашему нейрону:

\[z^{(L)} = w^{(L)} a^{(L-1)} + b^{(L)}\] \[\frac{\partial z^{(L)}}{\partial w^{(L)}} = a^{(L-1)}\]

Собирая все вместе получаем:

\[\frac{\partial C}{\partial w^{(L)}} = a^{(L-1)} \sigma ' ( z^{(L)} ) 2(a^{(L)} - y)\]

Эта формула показывает нам, как увеличение этого конкретного веса в последнем слое повлияет на стоимость этого конкретного обучающего примера. Это всего лишь одна очень специфическая информация, и нам нужно будет рассчитать гораздо больше, чтобы получить полный вектор градиента.

Но хорошая новость заключается в том, что мы уже заложили основы для остальной работы, которую необходимо проделать. Теперь это просто процесс обобщения наших результатов до тех пор, пока мы не получим представление (в виде вектора градиента) о том, как все веса и смещения в сети влияют на общую стоимость.

Вычисление производной по смещениям последнего слоя

Хорошей новостью является то, что чувствительность функции ошибки к изменению смещения практически идентична уравнению для изменения веса.

Напомним, что вот уравнение, которое мы нашли ранее для производной по отношению к весу в последнем слое: А вот и новое уравнение для производной по смещению в последнем слое (вместо веса):

\[\frac{\partial C}{\partial w^{(L)}} = \frac{\partial C}{\partial a^{(L)}} \cdot \frac{\partial a^{(L)}}{\partial z^{(L)}} \cdot \frac{\partial z^{(L)}}{\partial w^{(L)}}\] \[\frac{\partial C}{\partial b^{(L)}} = \frac{\partial C}{\partial a^{(L)}} \cdot \frac{\partial a^{(L)}}{\partial z^{(L)}} \cdot \frac{\partial z^{(L)}}{\partial b^{(L)}}\]

К счастью, эта новая производная равна просто 1:

\[z^{(L)} = w^{(L)} a^{(L-1)} + b^{(L)}\] \[\frac{\partial z^{(L)}}{\partial b^{(L)}} = 1\]

Так что производная по смещению оказывается еще проще, чем производная по весу.

\[\frac{\partial C}{\partial b^{(L)}} = \sigma ' ( z^{(L)} ) 2(a^{(L)} - y)\]

Это две записи с градиентом, о которых мы позаботились.

Зависимость от предыдущих слоев

Теперь мы определили, как изменения последнего веса и последнего смещения в нашей суперпростой нейронной сети повлияют на общую стоимость, а это значит, что у нас уже есть две записи нашего вектора градиента.

Все остальные факторы влияния и погрешности находятся на более ранних уровнях сети, что означает, что их влияние на стоимость менее прямое. Способ, которым мы с ними справляемся, заключается в том, чтобы сначала увидеть, насколько стоимость чувствительна к значению этого нейрона в предпоследнем слое, a(L-1), а затем увидеть, насколько это значение чувствительно ко всем предыдущим весам и смещениям.

Неудивительно, что производная от стоимости этой активации выглядит очень похожей на то, что мы уже видели:

\[\frac{\partial C}{\partial a^{(L-1)}} = \frac{\partial C}{\partial a^{(L)}} \cdot \frac{\partial a^{(L)}}{\partial z^{(L)}} \cdot \frac{\partial z^{(L)}}{\partial a^{(L-1)}}\]

\[z^{(L)} = w^{(L)} a^{(L-1)} + b^{(L)}\] \[\frac{\partial z^{(L)}}{\partial a^{(L-1)}} = w^{(L)}\]

Но на самом деле нас не волнует, что произойдет, когда мы изменим активацию напрямую, потому что у нас нет контроля над этим. Все, что мы можем изменить, пытаясь улучшить сеть с помощью градиентного спуска, - это значения весов и смещений.

Хитрость здесь в том, чтобы помнить, что активация на предыдущем слое на самом деле определяется его собственным набором весов и смещений. На самом деле наше дерево простирается дальше, чем мы показывали до сих пор:

###

\[C = \frac{1}{n} \sum_{k=0}^{n-1} C_k\] \[\frac{\partial C}{\partial w^{(L)}} = \frac{1}{n} \sum_{k=0}^{n-1} \frac{\partial C_k}{\partial w^{(L)}}\]

![]https://3b1b-posts.us-east-1.linodeobjects.com/content/lessons/2017/backpropagation-calculus/complicated-activation-labels.png()

Программная реализация

Пример