Вывод и предсказания. Часть 2: статистика
В первой части этой серии статей мы создали простую нейронную сеть (персептрон) для моделирования проблемы рейтинга кликов (CTR) для веб-сайта с заявлениями о приеме на работу. В конце нашего процесса мы осознали ограничения предсказания и классификации для решения проблемы, связанной с моделированием CTR. Самое большое озарение, которое мы получили, заключалось в том, что настоящая цель, моделирование ставки, заключалась в том, чтобы понять свойства самой модели, а не ее результат.
В этой следующей части нашей серии мы сосредоточимся на проблеме логического вывода, которая обычно является областью статистики. Когда мы делаем вывод, нас гораздо больше интересуют свойства самой модели, а не только ее прогнозы. Поскольку цель этой серии - показать связь между машинным обучением и статистикой, мы продолжим наш пример с того места, где остановились, создавая все части нашей статистической модели с нуля.
Продолжаем о модели машинного обучения
В качестве напоминания давайте вернемся к процессу, который мы разработали в прошлый раз, и посмотрим, как он может напрямую привести нас к статистической модели.
Мы начали с набора данных, представляющего информацию о пользователях веб-сайта, которые просматривали вакансии и либо подавали заявки, либо нет. Это список имеющихся у нас функций, охватывающий информацию о сходстве различных частей поиска с публикацией, возрасте публикации и категории, в которой была опубликована вакансия (у нас также есть константа для целей моделирования):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
features
> [' main_query_tfidf ',
'query_jl_score',
'query_title_score',
'job_age_days',
'job_16140',
'job_31542',
'job_41757',
'job_42467',
'job_45300',
'job_51966',
'job_67237',
'job_69982',
'job_77312',
'job_82238',
'job_other',
'const']
Эти функции находятся в матрице X и сопровождают вектор y результатов. Оба они были разделены на наборы данных для тестирования и обучения.
Наша модель представляла собой персептрон, который мы можем представить как:
\[y = g(X w)\]Где g - нелинейная функция (мы выбираем логистическую функцию), а w - набор весов. В коде модель выглядит так:
1
prediction = logistic (jnp.dot (X_train, w))
Мы также исследовали, как на самом деле обучается машинное обучение. Чтобы оптимизировать веса, мы использовали отрицательное логарифмическое правдоподобие и градиентный спуск, чтобы найти такие значения весов, которое оптимизирует вероятность того, что данные будут предоставлены нашей моделью. JAX сыграл важную роль в процессе, упростившем вычисление производных. Мы снова будем использовать эти методы в этом посте.
Теперь мы можем перейти к рассмотрению этого как статистической проблемы.
Вывод - статистический подход
Опираясь на библиотеки и программные пакеты, мы обычно используем разные инструменты для машинного обучения и статистики. Для работы с машинным обучением, которую мы проделали в предыдущем посте, полезные пакеты для решения этой проблемы могут включать scikit-learn или Keras, тогда как для статистической работы мы будем использовать такую библиотеку, как statsmodels. Хотя эти инструменты чрезвычайно полезны, они могут скрыть связь между статистикой и машинным обучением. Написав эти инструменты сами с нуля, мы увидим, насколько они близки. Фактически, чтобы продолжить моделирование для статистики, мы можем начать именно с того места, где остановились, нам просто нужно немного изменить нашу точку зрения.
Персептрон, который мы построили в первой части, идентичен логистической регрессии. При статистике мы не просто рассматриваем наши характеристики и веса в качестве входных данных, чтобы помочь нам предсказать результат, но и реальную модель того, как устроен мир. Вот изображение, которое показывает, как мы можем переосмыслить наш перцептрон из прошлого раза:
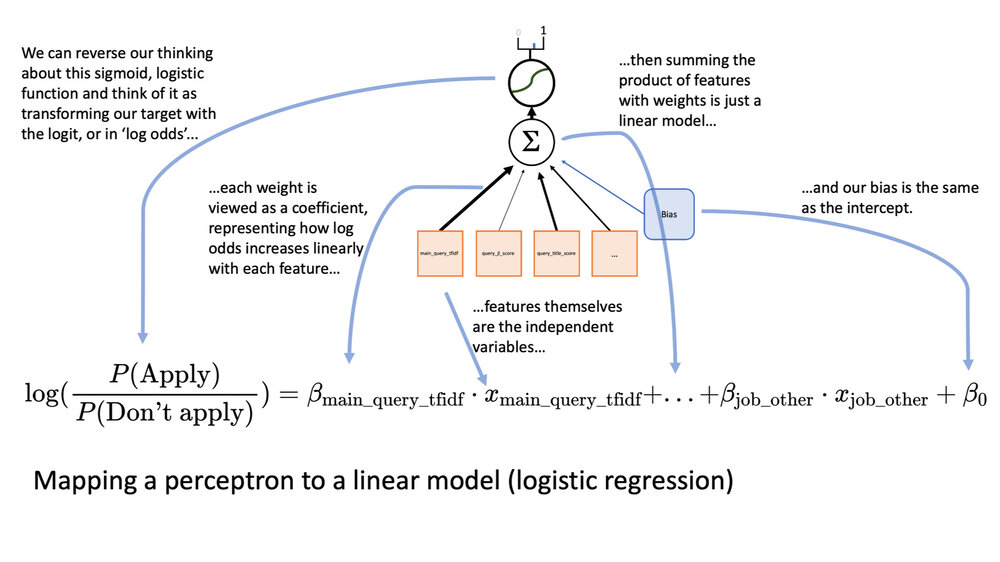
Хотя перцептрон может ощущаться совершенно иначе, чем логистическая регрессия, их реализация идентична.
В статистике мы представляем каждый из весов как коэффициент в нашей формуле, а единица смещения от персептрона становится свободным коэффициентом в линейном уравнении. Модель гласит, что каждый признак имеет линейную связь с логическими шансами пользователя, подавшего заявку на вакансию. Если вы хотите немного глубже понять, вот более ранний пост для понимания взаимосвязи между теоремой Байеса и логистической регрессией.
Это означает, что мы создаем модель, которая поможет нам понять, как каждая из функций может повлиять на вероятность того, что пользователь подаст заявку на работу на веб-сайте.
Что означают коэффициенты модели?
Самое первое, что мы хотим спросить после обучения нашей модели: «Что мы узнали о наших коэффициентах?» Мы можем поместить их в датафрейм и начать изучать:
1
2
3
stats_df = pd.DataFrame ()
stats_df ['feature'] = features
stats_df ['coef'] = w
Теперь мы можем взглянуть на то, что узнали. Эти коэффициенты может немного сложнее понять так как они представляют логарифмическую вероятность, но мы можем играть с этим немного чтобы получить лучшее представление:
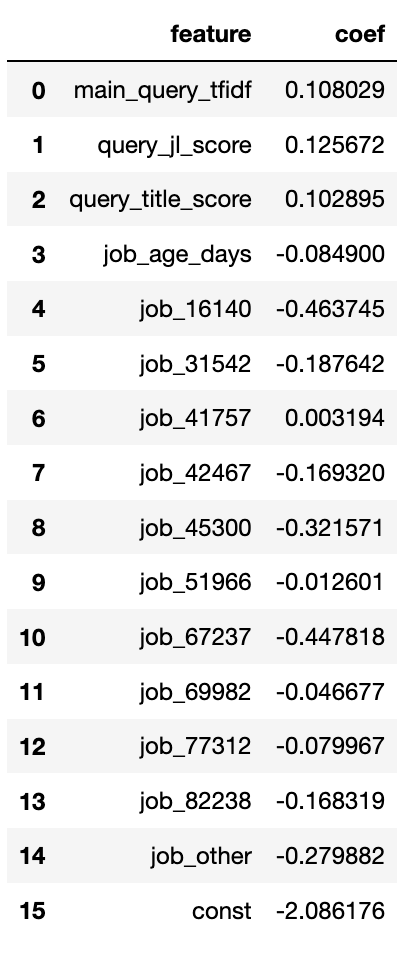
В качестве общего руководства: положительные значения означают, что по мере увеличения значения данного признака увеличивается и частота возникновения целевого события. Например, query_title_score показывает, насколько название должности похоже на строку запроса (чем выше, тем больше похоже). Мы видим, что этот коэффициент положительный, что означает, что чем больше название вакансии похоже на поиск пользователя, тем больше вероятность того, что пользователь подаст заявку.
Сразу видно, что в этом есть смысл. Если бы это значение было отрицательным, это было бы удивительно и противоречило нашей интуиции. Это одна из причин, по которой даже при прогнозировании важен логический вывод. Если это значение было отрицательным, возможно, мы ошибаемся в том, как устроен мир … или, может быть, в нашем коде есть ошибка.
Отрицательные значения означают обратное. Коэффициент для job_ages_days отрицательный, что означает, что чем старше публикация, тем меньше вероятность того, что пользователь подаст заявку.
Поскольку мы стандартизирован большинство наших значений (кроме категорий должностей), это означает, что значение 0 эквивалентно с_реднему значению этого признака_. Это полезно, потому что означает, что мы можем игнорировать многие из наших коэффициентов, когда хотим сравнить значения (мы увидим это чуть позже).
Мы также нормализовали наши значения путем деления на стандартное отклонение, что означает, что мы можем более или менее судить о важности характеристики по абсолютной величине коэффициента. Например, чтобы компенсировать негативное влияние нахождения в категории вакансий job_16140, вам понадобится query_title_score примерно на 4 стандартных отклонения от среднего значения лучше среднего!
Наш свободный коэффициент (здесь ‘const’), когда все наши функции нормализованы, становится логарифмической априорной вероятностью подачи заявки пользователем (вот целый пост об априорной вероятности в логистической регрессии). Мы не совсем все нормализовали, но достаточно близко, чтобы увидеть это. Мы можем использовать логистическую функцию, чтобы преобразовать логарифмические шансы обратно в вероятности. Давайте посмотрим, какой должна быть априорная вероятность в этой модели:
1
2
logistic(-2,086176)
> DeviceArray (0,11044773, dtype = float32).
Вы можете видеть, что она не сильно отличается от доли единиц в наших обучающих данных (если мы центрировали все, это было бы еще ближе):
1
2
y_train.sum () / y_train.shape [0]
> DeviceArray (0.08990832, dtype = float32)
Мы можем использовать эту модель, чтобы ответить на простые вопросы, которые могут возникнуть об ожидаемом поведении нашего сайта вакансий . Предположим, что кто-то, управляющий учетными записями, относящимися к job_16140, пришел и спросил вас:
По какой ставке я должен сказать клиентам, люди будут подавать заявки?
Мы можем очень легко это оценить. Поскольку все наши функции, не относящиеся к категории вакансий, имеют среднее значение по центру, в среднем они будут равны нулю, поэтому мы можем их игнорировать. Категории должностей являются взаимоисключающими, поэтому единственными значениями в нашей модели будут свободный коэффициент и 1 для job_16140. Это означает, что наш ответ:
1
2
logistic (-0,463745 + -2,086176)
> DeviceArray (0,0724318, dtype = float32)
Теперь пора перейти к самому важному вопросу статистики: насколько мы уверены в этом?
Измеряя неопределенность
Каждый из коэффициентов, полученных нашей моделью, является лишь точечной оценкой. Мы узнали это, найдя набор весов, который дает наиболее вероятное объяснение результатов с учетом данных, но что, если бы у нас было больше данных? И разве немного другой коэффициент не может достаточно правдоподобно объяснить данные?
В машинном обучении мы рассматриваем каждую из этих оценок как конкретное значение, но в статистике мы рассматриваем их как среднее значение нормального распределения возможных оценок. Теперь нам нужно вычислить стандартное отклонение этих распределений, в данном случае обычно называемое стандартной ошибкой.
Стандартная ошибка отрицательного логарифмического правдоподобия
Существует действительно интересная связь между нашей целевой функцией, отрицательной логарифмической вероятностью и стандартной ошибкой. Напомним, что мы нашли оптимальные веса, используя первую производную отрицательного логарифмического правдоподобия для оптимизации. Оказывается, мы можем использовать вторую производную этой функции, чтобы определить, насколько мы уверены!
Поскольку в качестве функции оптимизации мы использовали отрицательное логарифмическое правдоподобие, оказалось, что квадратный корень из обратной диагонали гессиана дает нам стандартную ошибку наших коэффициентов. Это много, поэтому давайте рассмотрим это в коде!
Сначала нам нужно получить гессиан, который представляет собой ужасающее название матрицы, представляющей вторую частную производную нашей функции, что само по себе является довольно пугающим способом сказать, «насколько широки кривые нашей функции в больших измерениях». Разве вы не рады, что у нас есть JAX?
Вот эффективная реализация JAX для эффективного вычисления Гессе:
1
2
3
from jax import jacfwd, jacrev
def hessian(f):
return jacfwd(jacrev(f))
Теперь нам нужно получить гессиан в точке, где мы нашли оптимальные веса, а именно:
1
2
3
our_hessian = hessian (lambda w: neg_log_likelihood (y_train, X_train, w)) (w)
our_hessian.shape
> (16, 16)
Как видите, это матрица размером 16 x 16, представляющая как изменяется каждый вес при изменении другого. Для вычисления наших стандартных ошибок все, что нас волнует, - это диагональ этого (потому что мы предполагаем, что каждый коэффициент не зависит от других):
1
our_hessian_diag = jnp.diag (our_hessian)
Обратное к этому дает нам нашу дисперсию …
1
coef_variance = 1/ our_hessian_diag
И, конечно же, мы бы не назвали это σ2, если бы нам не нужно было наше стандартное отклонение, а именно:
1
stats_df ["se"] = jnp.sqrt (coef_variance)
Наконец, мы можем увидеть, как наши стандартная ошибка наших коэффициентов:
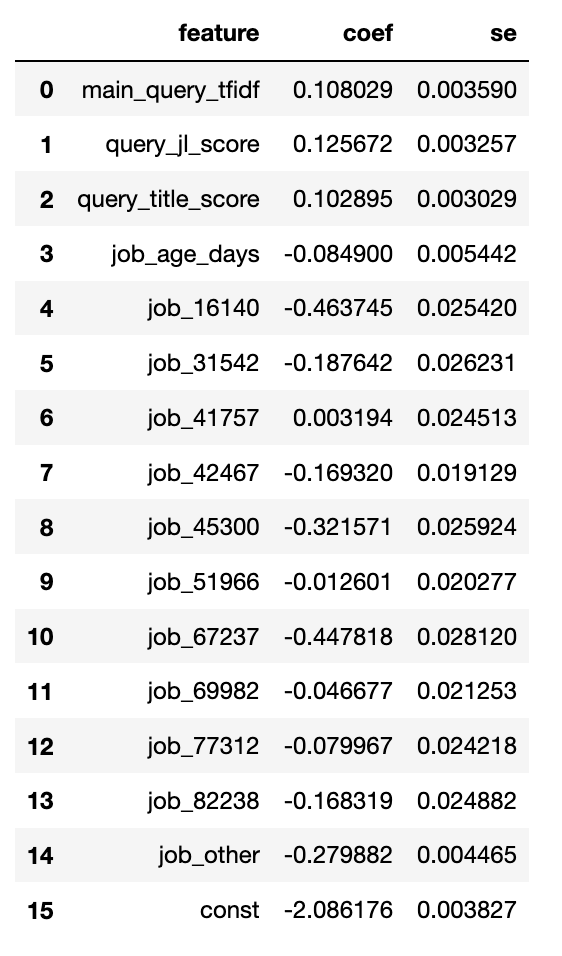
Это было совсем немного работы, но теперь вся остальная статистика выпадает из этого почти тривиально!
Остальные статистики: z-оценки, p-значения, доверительные интервалы
После вычисления стандартной ошибки удивительное количество статистики может быть получено с помощью относительно простых преобразований. Мы начнем с вычисления z-оценки, которая, по сути, показывает, на сколько стандартных отклонений от нормального распределения со средним значением 0 будет наше наблюдаемое среднее значение. Это очень просто вычислить:
1
stats_df ['z-score'] = stats_df ['coef'] / stats_df ['se']
P-значения измеряют вероятность того, что z-оценка будет стандартным отклонением от среднего. Мы можем легко вычислить это как:
1
2
3
4
from jax.scipy.stats import норма
from jax import vmap
stats_df ['p-value'] = 2.0* (1.0-vmap (norm.cdf) (
jnp.array (stats_df ['z-score'] .abs ())))
Лично я не большой поклонник p-значения, но они могут быть очень полезны для быстрого обобщения результатов нашей регрессии. Что они сбивают с толку, так это «вероятность того, что мы получили этот результат, если истинное значение коэффициента было ровно 0».
Намного более полезным является то, что мы хотели бы иметь нижнюю и верхнюю границы для нашей оценки для 95% доверительного интервала. Здесь я использую термин «доверительный интервал», чтобы обозначить, что мы на 95% уверены, что истинное значение находится где-то между нижней и верхней границей (lb и ub):
1
2
stats_df ['lb'] = stats_df ['coef'] - stats_df ['se'] *2
stats_df ['ub'] = stats_df ['coef'] + stats_df ['se'] *2
И теперь у нас есть все основные результаты, которые вы ожидаете от такого инструмента, как statsmodels:
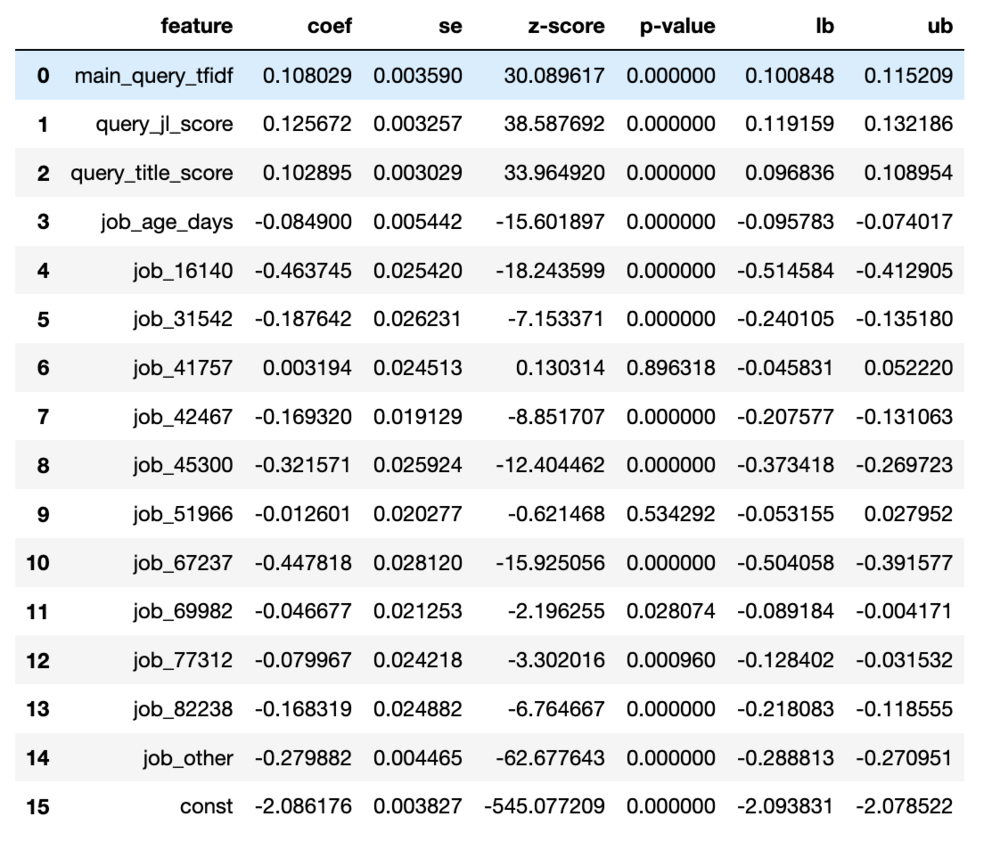
Стоит уделить время тому, чтобы поразмыслить, как далеко мы ушли от прошлого поста, и при этом следить за непрерывным потоком небольших изменений в нашей первоначальной работе над персептроном!
Тестирование гипотезы и оценка параметров
В том, что мы узнали об этих коэффициентах, содержится удивительное количество важной статистической информации. Мы можем трактовать эту информацию немного по-разному, чтобы прийти к нашим данным с точки зрения частотности или байесовской точки зрения. Мы можем визуализировать все эти свойства для коэффициента job_69982:
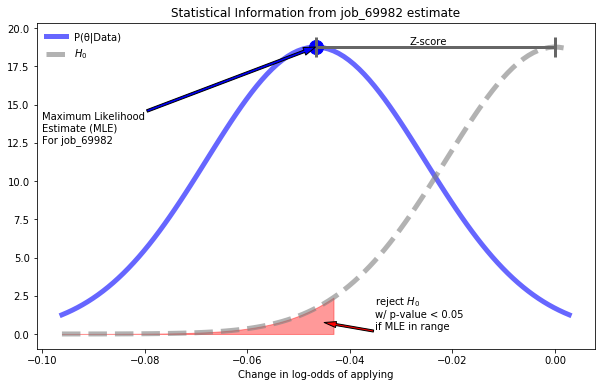
Мы можем визуализировать все, что мы узнали о наших весах.
Понимая различные интерпретации свойств, которые мы видим здесь, мы можем использовать нашу модель как твердую отправную точку для частотного или байесовского анализа.
Частотное тестирование гипотезы
С точки зрения частотности p-значения каждого коэффициента говорят нам, следует ли нам отвергать нулевую гипотезу H0. В этом конкретном случае нулевая гипотеза состоит в том, что коэффициент равен 0. В конкретном случае job_69982 мы можем просмотреть результаты здесь как пример проверки значимости нулевой гипотезы, где мы проверяем, имеет ли job_69982 влияние на пользователя, применяющего. При p-значении 0,028074 мы отклонили бы нулевую гипотезу, учитывая общий порог значимости 0,05.
Если вы когда-нибудь находили статистику сложной дл японимания, вас ждет счастливый сюрприз. Практически каждый частотный статистический тест можно смоделировать как некоторую вариацию нашей линейной модели!
С небольшим преувеличением можно сказать, что в нашем продолжении примера машинного обучения мы по существу охватили большую часть классической статистики.
Байесовское оценивание параметров
Байесовцы гораздо меньше озабочены тем, равен ли коэффициент нулю, и вместо этого сосредотачиваются на том, каким, по нашему мнению, может быть на самом деле значение. То есть мы сосредоточены на оценке параметров. С байесовской точки зрения мы рассматриваем w как вектор наших параметров, обычно обозначаемый как θ. В байесовском анализе мы всегда пытаемся решить нашу проблему в терминах теоремы Байеса:
\[P(\theta | Data) = \frac{P(Data|\theta)P(\theta)}{P(Data)}\]обратите внимание, что P(Data∣θ) - это вероятность, которая напрямую связана с нашей функцией потерь. Если мы предположим единообразную априорность для P(θ) (что-то, с чем мы можем поиграть, изменив в части 3), то мы увидим, что машинное обучение также изучало, является именно этой точной моделью.
Как байесовцы, мы смотрим на P(θ∣Data) как на распределение убеждений, которое в этой модели на самом деле является многомерным нормальным распределением с вектором средних значений, равным w, и диагональной матрицей Σ, соответствующей изученному нами se. В этом случае мы рассматриваем нижнюю и верхнюю границы каждого параметра как пределы того, что, по нашему мнению, может быть реалистичным значением для этого параметра.
Таким образом, наша модель обеспечивает основу для начала понимания нашей проблемы как с частотной, так и с байесовской точки зрения! Здесь мы можем увидеть мудрость минимизации отрицательной логарифмической вероятности, поскольку это позволяет нам связать машинное обучение с двумя разными взглядами на статистику в одной модели. Теперь мы исследуем, как мы можем использовать все это, чтобы начать решать проблемы, связанные с CTR.
Проведение экспериментов
При моделировании всегда важно, чтобы наши усилия были близки к нашим реальным целям. В этой серии сообщений мы просто заявили, что проблема заключается в «моделировании CTR», но для чего?
Предположительно, если бы мы были компанией, которая перечисляла объявления о вакансиях, и мы заботились бы о ставке, которую соискатели применяют к объявлениям, мы бы хотели увеличить эту ставку. Взгляд на нашу модель помогает нам подумать о том, как мы начали бы решать эту проблему. Посмотрев на нашу модель, мы можем увидеть, что мы очень уверены в том, что query_title_score имеет большое влияние на частоту, которую применяют люди.
Это сразу же наводит нас на мысль:
Если есть способ увеличить среднее сходство между названием должности и запросом, это должно увеличить процент подачи заявок?
Это приводит нас к следующему вопросу «как мы можем это сделать?»
Всегда спрашивайте, что это значит,
Но прежде чем приступить к решению этой проблемы, очень важно, чтобы мы всегда задавались вопросом, что модель говорит нам о мире, и можем ли мы сформировать какое-либо связное понимание вокруг этого.
Например, однажды я работал в компании, которая пыталась повысить продажи менее популярных товаров, подняв их выше в результатах поиска. С чисто модельной точки зрения это имеет смысл: товары с лучшими позициями продаются лучше. Но он не дает ответа на вопросы о том, почему товары вообще находятся в лучшем положении: как правило, это потому, что они лучше продаются. Когда мы проводили этот эксперимент, за некоторыми исключениями, мы обычно обнаружили, что товары не работали лучше (в некоторых случаях они работали хуже!), когда их искусственно перемещали на лучшие позиции.
Итак, в нашем случае мы должны спросить себя: почему мы думаем, что может возникнуть большая разница между названием должности и запросом, и дает ли любой из этих случаев возможность исправить настоящую проблему.
Один случай может заключаться в том, что кто-то ищет “Data Scientist”, а результат - “Accountant”. Предположим, это происходит из-за того, что в описании есть слова «ввод данных» и «бакалавр наук». В этом случае слова другие, равно как и их значения. Если мы каким-то образом искусственно изменим название должности для лучшего соответствия, мы только расстроим пользователя.
Однако другой случай, когда пользователь выполняет поиск «специалист по данным» и появляется «Associate Researcher (ML)». Предположим, что «Associate Researcher (ML)» на самом деле то же самое, что и специалист по данным, но пользователь сбит с толку и поэтому не подает заявку.
Оба этих сценария правдоподобны, я лично считаю, что первый более вероятен, но реальная сила статистики в том, что нам не нужно спорить о том, какое влияние произведут изменения, мы можем проверить!
Тестирование предлагаемых решений
Для решения этой проблемы команда машинного обучения разработала умную модель обработки естественного языка, которая переписывает названия должностей, чтобы иметь более высокую вероятность совпадения с семантически похожими поисковыми запросами. Это отличная новость, но очевидный вопрос, который нам нужно задать, - это «действительно ли это работает?».
Чтобы протестировать нашу модель переписывания заголовков, мы решаем провести контролируемый эксперимент. Мы назначим 20% наших пользователей в тестовую группу, где заголовки в результате будут переписаны на основе запроса, а у остальных будет такой же опыт, как и раньше.
После некоторого запуска эксперимента у нас есть новый набор данных: X_exp и y_exp. Они используют ту же настройку, что и наши исходные данные, с одной новой функцией, показывающей, был ли пользователь “in_test”.
Теперь мы действительно можем увидеть красоту моделей, интерпретируемых как последовательность гипотез о влиянии коэффициента. Прежде чем строить модель с данными нашего эксперимента, мы должны сначала подумать о том, что мы надеемся увидеть в результатах.
Наша цель состоит в том, чтобы пользователи из нашей тестовой группы подавали заявки с большей скоростью, чем все остальные. Итак, мы хотим видеть, что наш коэффициент положительный. С точки зрения классической статистики мы хотим, чтобы p-значение было очень маленьким (даже байесовцы могут использовать это как полезную эвристику). Если это произойдет, это означает, что у нас есть веские доказательства того, что наша логика перезаписи заголовка сработала!
Чтобы проанализировать наши результаты, мы можем построить новую версию нашей модели с дополнительными коэффициентами, показывающими, был ли пользователь в тестовой группе. Обратите внимание, что теперь, когда мы выполнили всю работу по созданию наших необходимых функций, создание этой новой модели с нуля не так уж и много:
1
2
3
4
5
6
7
8
9
10
key = random.PRNGKey (123)
w_exp = random.uniform (key,
shape = (X_exp .shape [1],),
minval = -0,1,
maxval =0,1)
lr = 0,000001
for _ in range(1,300):
w_exp - = lr * d_nll_wrt_w_c (y_exp, X_exp, w_exp)
print (neg_log_likelihood (y_exp, X_exp , w_exp))
> 257385.67
После повторения процесса построения датафрейма статистики у нас есть следующие результаты:
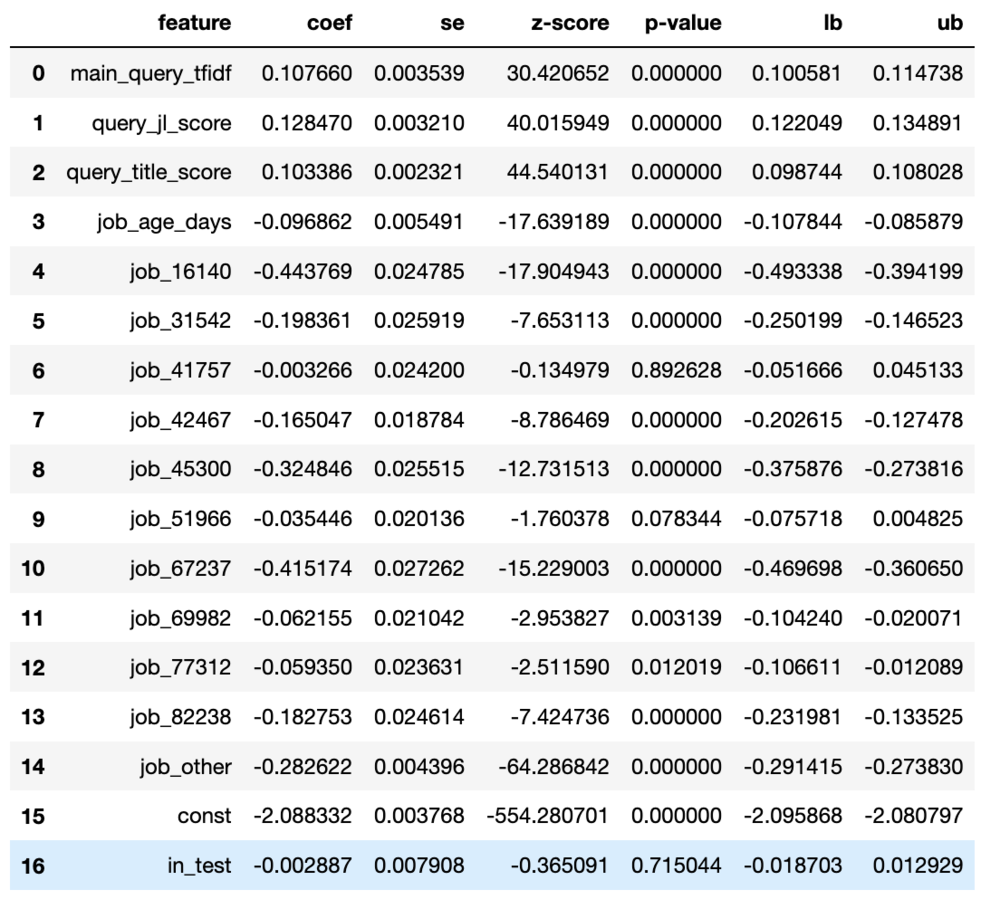
Глядя на результаты наших тестов, можно сказать, что они выглядят не слишком обнадеживающе для нашего нового инструмента перезаписи.
Когда мы смотрим на результаты для in_test, они выглядят плохо. Коэффициент немного отрицательный (хотя и очень незначительно), но, что хуже всего, p-значение велико.
P-значения не говорят нам всего, может быть, просто недостаточно данных? Мы можем понять это, посмотрев на нижнюю и верхнюю границы нашей оценки. Если это большие числа, это означает, что существует большая неуверенность в том, какое значение может быть на самом деле, а это значит, что мы действительно не знаем. К сожалению, в этом случае эти числа довольно близки к 0, что статистически означает, что наш умный переписчик заголовков, вероятно, не работает …
… за исключением того, что мы упускаем важную часть головоломки моделирования!
Причинность
Здесь мы видим наглядный урок того, почему для нас так важно понимать, что, по нашему мнению, произойдет, когда мы проведем наш эксперимент. Вначале мы заявили, что наш редактор заголовка должен увеличить query_title_score, но мы включили query_title_score в нашу модель. Поскольку единственное влияние, теоретически оказываемое переписчиком, заключалось в улучшении query_title_score, контроль этого в нашей модели скроет влияние, которое оказал тест!
То есть существует причинно-следственная связь между тестом и query_title_score, наблюдая query_title_score в нашей модели, мы удаляем любую информацию, которую мы получили о тесте.
Чтобы решить эту проблему, нам нужно перестроить модель, у которой нет query_title_score.
Вот код для этого:
1
2
3
4
5
6
key = random.PRNGKey (123)
X_exp_no_qs = jnp.array (np.delete (X_exp,2, axis =1))
w_exp_no_qs = random.uniform (key,
shape = (X_exp_no_qs.shape [1],),
minval = -0.1,
maxval =0.1)
Мы пропустим код для обучения, поскольку мы уже видели его несколько раз, и проверим, что наш коэффициент in_test говорит нам теперь, когда мы правильно моделируем причинно-следственную связь:

Теперь, когда мы правильно моделируем нашу проблему, мы видим, что результаты значительны!
И теперь мы видим, что in_test имеет строго положительное значение с чрезвычайно низким значением p. Теперь мы почти уверены, что наш переписчик удался!
Однако наша первоначальная экспериментальная модель не бесполезна. Если вы знаете, что обработка должна влиять на один из коэффициентов модели, я всегда рекомендую посмотреть, может ли включение этой функции устранить значимость тестового коэффициента (или значительно снизить ее). Это очень помогает при отладке экспериментов. Если бы мы включили query_title_score, а in_test все еще был значимым, это означало бы, что есть что-то еще, не контролируемое в модели, что заставляло нашу тестовую группу работать лучше. У меня такое случалось в прошлых экспериментах, и это жизненно важный инструмент для правильного выполнения тестов.
Сравнение моделей по критерию Акаике
Поскольку в последнем разделе мы построили две модели, неплохо уделить время обсуждению того, как мы сравниваем модели в статистике. В машинном обучении нас в первую очередь интересуют выходные данные модели, поэтому мы придумываем различные метрики, чтобы сравнить прогнозы модели с наблюдаемыми результатами. В статистике нас в первую очередь интересуют параметры и сложность модели.
Обычное измерение для оценки моделей в статистике - это некоторая форма информационного критерия, который уравновешивает вероятность данных, заданных в модели, со сложностью модели. Наиболее распространенным является информационный критерий Акаике (AIC). В случае, когда k - количество параметров в модели, а L - вероятность, AIC определяется как:\
\[AIC = 2 k -2 ln(L)\]Поскольку мы используем отрицательную логарифмическую правдоподобие, мы бы просто имели:
\[AIC = 2 k - 2 nll\]Абсолютное значение этой метрики не имеет значения, но в целом, чем меньше баллов, тем лучше, когда мы сравниваем модели, обученные на одних и тех же данных. Обычно мы хотим, чтобы при добавлении параметров мы уменьшали AIC. Мы можем увидеть, как работали наши модели:
1
2
3
4
5
6
7
8
def aic (y, X, w):
k = X.shape [1] -1
nll = neg_log_likelihood (y, X, w)
return 2 * k + 2 * nll
aic (y_exp, X_exp, w_exp)
> 514803,34
aic (y_exp, X_exp_no_qs, w_exp_no_qs)
> 515627,5
Мы видим, что добавление оценки запроса обеспечивает гораздо более низкий AIC. Это означает, что добавление только этого одного параметра к нашей модели значительно повысило правдоподобие. Единственная причина, по которой нам нужно было удалить эту важную функцию, заключалась в том, что она влияла на нашу способность понимать результаты нашего теста.
На пути к синтезу
Основным ограничением статистического вывода является то, что он традиционно имеет тенденцию избегать вычислительного мышления. Статистика на протяжении большей части своей истории не является предметом для хакеров. Статистическое программное обеспечение, как и статистические тесты, оставалось непрозрачным и загадочным. Студенты, изучающие статистику, могут формально вывести закрытое решение для версии регрессии МНК, но после этого все будет делаться некоторым стандартизированным пакетом программного обеспечения. Полагаться на абстракцию - это хорошо, но без возможности построения статистики с нуля мало места для игр, экспериментов и исследований.
Именно здесь машинное обучение и, в частности, глубокое обучение действительно проявили себя в последнее десятилетие. Посмотрите любое выступление экспертов в области машинного обучения, и вы почувствуете невероятную игривость. Я до сих пор помню волнение, с которым наблюдал за выступлениями Джеффри Хинтона в 2012 году. Почти все инновации, возникающие в результате глубокого обучения, исходят от кого-то, кто спрашивает: «Что произойдет, если мы попробуем это?»
Точно так же создание нейронной сети не является загадкой для практиков. Любой, кто серьезно интересуется нейронными сетями и машинным обучением, быстро получает опыт создания сети с нуля, а затем экспериментирует с этим дизайном, чтобы увидеть, что еще они могут сделать. Статистики могут критиковать глубокое обучение за его отсутствие строгости, и в этой критике есть определенная ценность, но отсутствие игры в статистике остается, пожалуй, самым большим ее недостатком.
Но теперь вы видите, как все работает в статистической модели, построенной на основе простой математики и линейной алгебры! В части 3 мы продолжим наше исследование, применив причинно-следственное исследование подхода машинного обучения, уделяя внимание пониманию наших моделей, которые мы получаем из мира статистических выводов. По правде говоря, между этими двумя понятиями нет разделения, только восхитительные возможности математических исследований.


