Вывод и предсказания. Часть 1: машинное обучение

Оригинал

Это первая статья из трех, посвященных разнице между выводом и предсказанием в моделировании данных. Также мы разберем разницу между машинным обучением и статистикой. За мою карьеру аналитика данных я обнаружил удивительное непонимание понятия вывода, который обычно понимается как часть статистики. Я также понял, что, хотя это менее распространено, профессиональные статистики не очень хорошо понимают, как машинное обучение ставит задачи предсказания.

Немногим более года назад я запостил картинку в Твиттере, которая отражает мое понимание этих понятий:

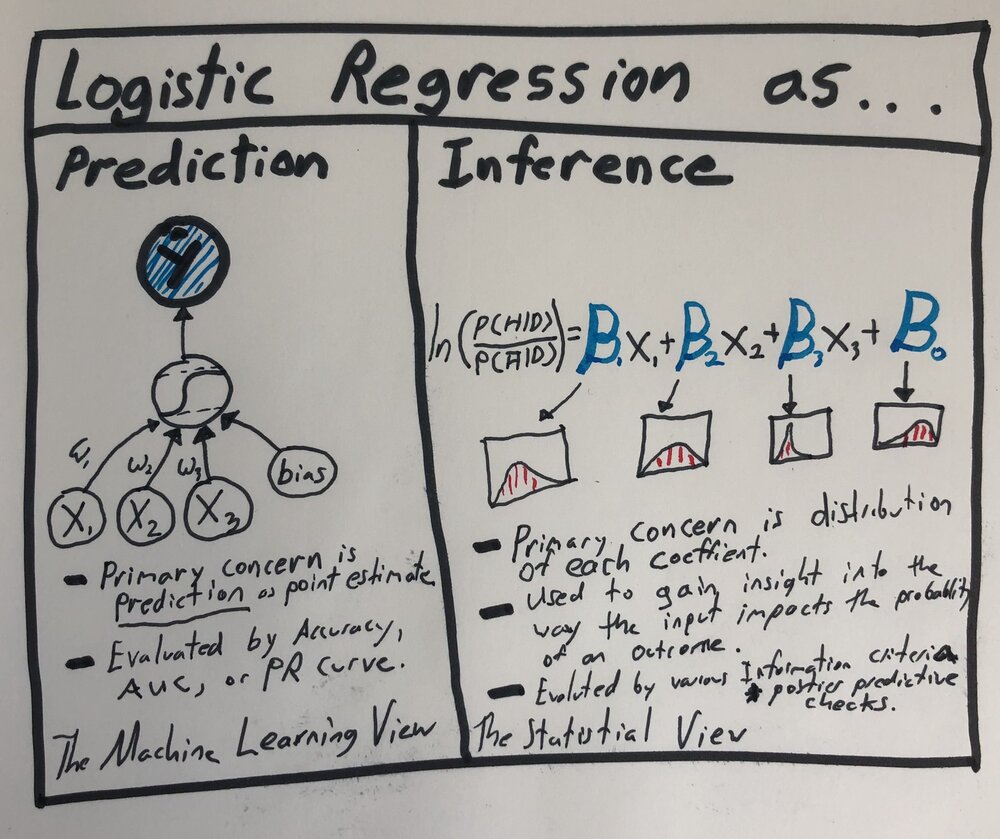
В этой серии статей мы увидим, что эти два понятия связаны больше, чем обычно представляют.

В первой статье я бы хотел не только наметить общую идею через рабочий пример, но и попытаться сблизить эти два понятия. Конечной целью каждого исследователя должно быть рассмотрение моделирование как системного процесса, использующего все возможности математических рассуждений. Процесс моделирования должен быть интерактивным, выходящим за рамки этих двух понятий, что особенно актуально в наш век доступных вычислительных возможностей.

Пример: моделирование доли пользовательского отклика

Одна из самых распространенных проблем в индустрии - это моделирование доли пользовательского отклика (Click Through Rate, CTR). Обычно проблема CTR возникает, когда мы оцениваем выполнение пользователем определенных действий: подписка на сервис через форму, щелчки по рекламе, просмотр описания товаров в каталоге, покупка товаров, чтение постов в агрегаторе, и так далее.

В предыдущей статье мы говорили о процессе сэмплирования Томпсона при оптимизации рекламных аукционов. Одна из ключевых частей той статьи была посвящена оценке CTR с помощью бета-распределения, зная только предыдущее соотношение кликов и просмотров. И хотя этот подход прекрасно работает, обычно у нас есть много дополнительной информации, которую можно использовать для более точного понимания пользовательского отклика.

В этом примере мы будем использовать информацию об откликах пользователей на объявления о вакансиях с сайта объявлений. Данные взяты из этого набора с Kaggle. Мы используем эти данные для моделирования того, откликнется ли пользователь на данное объявление о вакансии, исходя из его категории, и того, насколько соответствует заголовок объявления пользовательской строке запроса.

На протяжении всей моей карьеры в анализе данных меня удивляет то, насколько часто эти задачи трактуются как чисто предсказательные. Как мы увидим в этой статье, исключительно предсказательный подход к проблеме CTR приводит к ограниченности того, как можно решать разные задачи, относящиеся к этой проблеме (а именно, как повысить отклики!). Для начала мы подойдем к этой задаче с точки зрения машинного обучения, построив простой персептрон на Python и JAX, а затем, в следующей части, расширим эту модель для решения задачи вывода.

Взгляд на данные

Прежде чем мы начнем, взглянем на очищенные данные из нашего набора. Вот какие признаки мы будем использовать:

features = ['main_query_tfidf', 'query_jl_score',
            'query_title_score','job_age_days',
            'job_16140', 'job_31542','job_41757',
            'job_42467','job_45300','job_51966',
            'job_67237', 'job_69982', 'job_77312',
            'job_82238','job_other']

Первые три признака описывают разные метрики близости строки поиска пользователя и заголовка объявления о вакансии, следующий - возраст объявления в днях, а затем у нас идут 10 самых распространенных категорий объявлений как индикация того, принадлежит ли данное объявление к этой категории.

Вот как выглядят данные, уже приведенные к стандартному нормальному распределению:

apply_data[features]

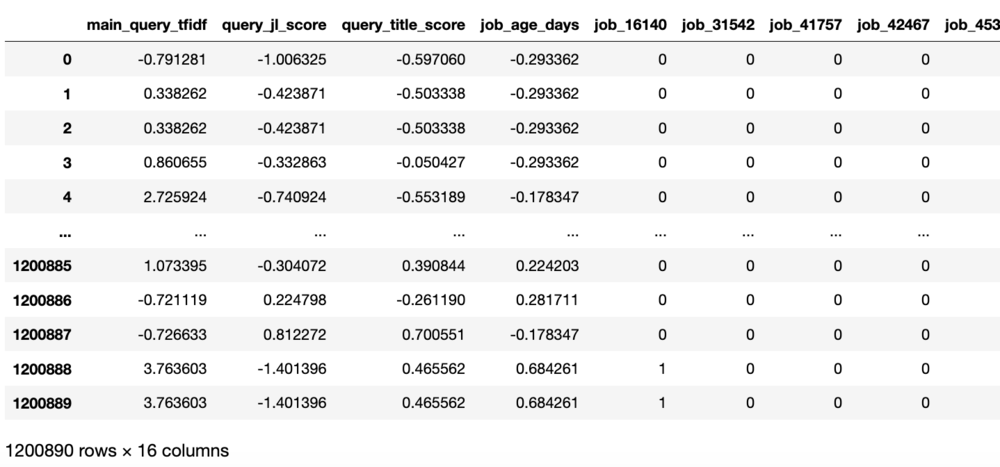
Как Вы видите, у нас достаточно данных - 1 200 890 строк.

Далее мы будем производить множество вычислений по этим данным, так что приведем их в формат матрицы jax и разделим на обучающую и тестовую выборки:

import jax.numpy as jnp
X = jnp.array(apply_data[features].values)
y = jnp.array(apply_data['apply'].values)
train_size = int(np.round(0.7*float(X.shape[0])))
indices = np.random.permutation(X.shape[0])
X_train, X_test = X[0:train_size], X[train_size:]
y_train, y_test = y[0:train_size], y[train_size:]

Теперь можем начинать моделирование!

Предсказание - подход машинного обучения

Теперь когда мы полностью подготовили данные, время заняться моделированием! Если вы опытный аналитик данных или эксперт по машинному обучению, большая часть этой статьи будет вам знакома. Это намеренно, так как я хочу показать логику, которая связывает традиционных взгляд с точки зрения машинного обучения со взглядом статистическим. Так что, хотя тема и знакома, стоит повторить, как именно мы думаем о решении проблем машинного обучения.

Так как мы занимаемся машинным обучением, хочется начать с нейронной сети. Но мы хотим начать с чего-то разумно простого, так что выберем самый простой тип нейронных сетей: персептрон. Если вы незнакомы с персептроном - это просто нейронная сеть без скрытых слоев. Вот иллюстрация нашей модели:

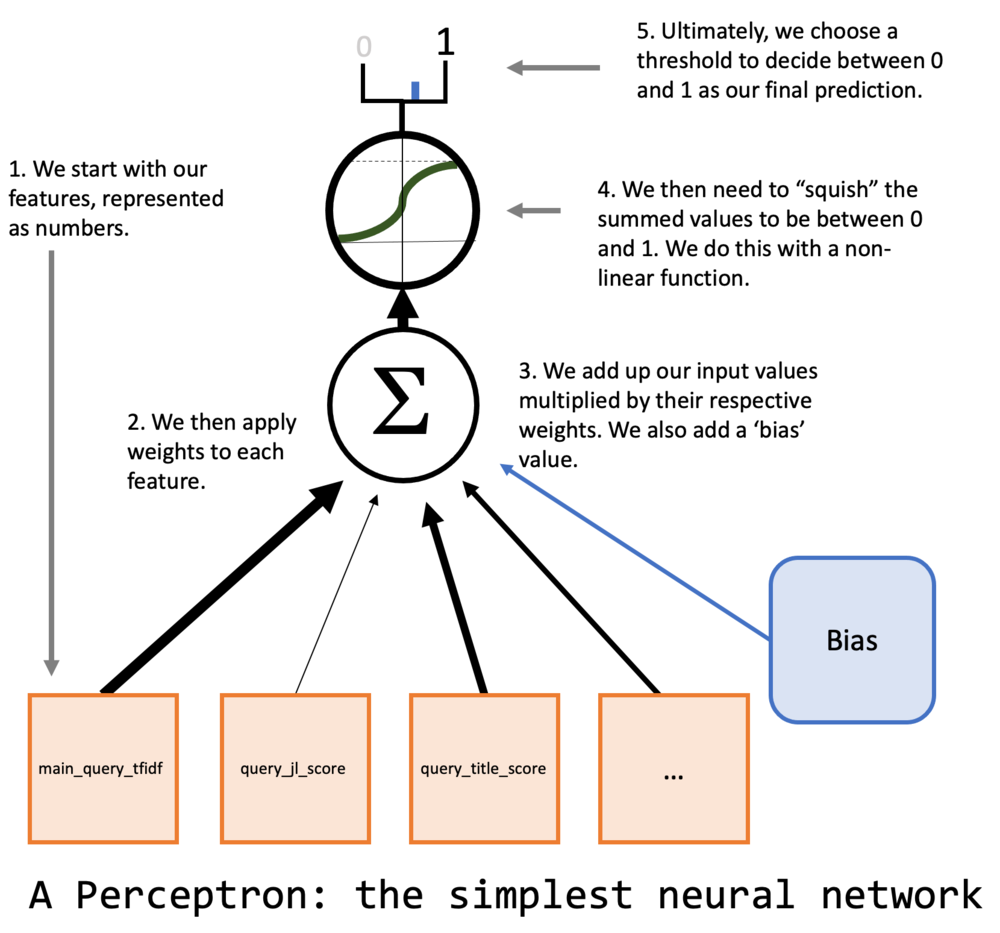
Обратите внимание на элемент “bias” или “смещение” на картинке. Мы можем его представить, добавив постоянный признак к нашему набору данных, что я уже сделал с массивами X_train и X_test.

Сборка модели воедино

Давайте подумаем о математике, лежащей в основе нашей модели. У нас есть графическое представление того, как устроен персептрон, на нам нужно понять, как заставить его работать в коде. У нас есть массивы X и y, то есть, соответственно, данные и целевая переменная. Нужно добавить кое-то еще.

Первый шаг - это представление всех линий на нашей диаграмме численно. Мы сделаем это с помощью вектора весов w. Но какие значения должны быть у этого вектора? Вот их как раз мы и хотим подобрать, или, как говорят, обучить (точнее мы хотим, чтобы машина их обучила).

Мы опять используем для этого jax, и для начала сгенерируем случайные веса. В отличие от обычного numpy, jax всегда требует ключ для генерации случайных значений. Это значит, что случайные переменные будут предсказуемыми. Это очень полезно при отладке нашей модели, ведь мы будем производить много случайных действий, а так они могут быть воспроизведены в точности. Вот пример того, как можно создать массив случайных весов:

from jax import random
key = random.PRNGKey(1337)
w = random.uniform(key, 
                   shape=(X_train.shape[1],), 
                   minval=-0.1,
                   maxval=0.1)

Линии на диаграмме соответствуют перемножению значений признаков данных с весами и их суммированию. Математически мы можем представить перемножение и суммирование очень просто при помощи линейной алгебры:

\[X w\]

В коде это тоже довольно просто получается:

jnp.dot(X_train,w)
> DeviceArray([0.15793219, 0.07844558, 0.07844558, ..., 0.27550998,
             0.10248479, 0.13946426], dtype=float32)

Но мы еще не закончили. Есть одна заметная проблема. Мы хотим предсказывать 1 (если пользователь откликнется на вакансию) или 0 (если нет), так что нам нужен способ убедиться, что все наши предсказания находятся в этом диапазоне. Для этого нам понадобится нелинейная функция, которая сожмет получаемые значения в диапазон от 0 до 1. Используя g для обозначения этой функции, мы можем представить полное математическое представление персептрона как:

\[y=g(X w)\]

Самым простым вариантом для g будет логистическая функция, которая как раз выдает значения от 0 до 1. Кроме того, выдаваемые ей значения могут быть интерпретированы как вероятности. Мы еще этого коснемся во второй части, но это важно для будущего обучения нашей модели. Вот математическое выражение логистической функции:

\[g(x) = \frac{1}{1+e^{-x}}\]

А вот то же самое в коде:

def logistic(val):
    return 1/(1+jnp.exp(-val))

Можем теперь применить это к X и случайным весам и получим нашу первую модель!

guesses = logistic(jnp.dot(X_train,w))
guesses
> DeviceArray([0.5394012 , 0.51960135, 0.51960135, ..., 0.5684451 ,
              0.52559876, 0.53480965], dtype=float32)

Это, по сути дела, именно случайные угадывания. Следующий шаг - попробовать улучшить их.

“Обучение” из машинного обучения

Конечно, наша модель пока ничего не знает о мире. Можно заметить, что она почти всегда выдает близке к 0,5 значения, ровно посередине между нашими вариантами 0 и 1. При предсказании мы обычно выбираем (точнее за нас выбирает программный инструмент) 0,5 как пороговое значение между этими вариантами. Так что пока примерно половина случаев будет определяться как предполагаемое наличие отклика, а половина - как отсутствие. Результат может немного отличаться из-за неравномерности распределения данных, но по сути мы просто умножаем равномерно распределенные случайные значения (веса модели) на значения, приведенные к стандартному распределению. Если подставить среднее значение - 0 в логистическую функцию, как раз и получается 0,5. Естественно, эти веса надо поменять со случайных на такие, которые лучшим образом преобразуют данные в нужный результат.

Можно иронизировать над названием “машинное обучение” для такого простого случая, но он даст нам хорошее описание используемых алгоритмов. Мы хотим, чтобы машина (то есть компьютер) обучилась лучшим w для нашей модели. Ключ к этому в том, чтобы дать понять машине, что один набор весов лучше или хуже другого. Мы добьемся этого, создав целевую функцию (ее еще называют функция потерь), которая определяет, насколько удачны изменения в модели.

Мы уже упоминали, что преимущество использования логистической функции в том, что мы может воспринимать ее значения как вероятности. Так значение 0,2 значит, что вероятность отклика на вакансию составляет 20%, а значение 0,75 - что 75%. Значения целевой переменной тоже так работают. Если мы знаем, что пользователь не ответил на вакансию, мы можем сказать, что вероятность ответа составила 0, а если ответил, то вероятность достоверного события равна 1.

Так можно понять, как сконструировать целевую функцию, которую мы будем оптимизировать. Если модель выдает 0.75, мы можем спросить, “Какова вероятность получения 1, если мы считаем, что вероятность отклика равна 75%?”

Очевидно, это просто 0,75. И наоборот, если модель выдает 0,75 а у нас записано 0, вероятность того, что модель верна всего 25%. Мы хотим получить такую функцию, которая вычисляет, насколько вероятны известные нам исходы при данных значениях весов. Как только мы ее получим, останется только найти веса, которые лучше всего объясняют известные нам данные. Это подход максимального правдоподобия для нахождения лучших весов.

Обоснование отрицательного логарифмического правдоподобия

Пока мы говорили о нахождении правдоподобие единственной точки данных, но нам нужен способ подсчитать это для всех 840 623 строк из обучающей выборки. Вот пример кода, который вычисляет правдоподобие данных при имеющихся весах для всего обучающего набора (p_d_h означает Probability of Data given the Hypothesis, вороятность данных при гипотезе):

y_prob = logistic(jnp.dot(X_train,w))
p_d_h = jnp.where(y_train == 1, y_prob, 1-y_prob)
print(p_d_h)
> [0.46059883 0.48039865 0.51960135 ... 0.4315549  0.47440124 0.46519035]

Каждое значение представляет, насколько вероятен наблюдаемый исход, если предположить, что модель верна.

Мы хотим объединить их все в единое значение правдоподобия данных для конкретной модели. Мы могли бы для этого просто перемножить их:

\[P(y \mid X w) = \prod^{N}_{i=1}{P(y_i \mid X w)}\]

Это соответствует полной вероятности всех наблюдений при верности нашей модели.

И хотя это математически корректно, можно быстро увидеть проблему:

jnp.prod(p_d_h)
> DeviceArray(0., dtype=float32)

Так как мы берем произведение более 800 000 вероятностей, полученный результат меньше минимального числа, которое может быть представлено в компьютере. Вероятность случайных весов получилась равна нулю, но даже если бы у нас была прекрасная модель, дающая, скажем, вероятность правильного прогноза 0,99, все равно получилось бы:

\[0,99^{840 623}\]

Что для компьютера все равно 0.

Хорошее решение этой проблемы - это взять логарифм каждой вероятности и суммировать их вместо того, чтобы перемножать. Это даст нам логарифмическое правдоподобие, что гораздо удобнее при использовании компьютера. Как мы видим, логарифмическое правдоподобие считается более содержательно:

jnp.sum(jnp.log(p_d_h))
> DeviceArray(-619300.56, dtype=float32)

Осталась одна проблема с этим значением. Обычно, оптимизационные алгоритмы находят минимальное значение выпуклой функции. Чем меньше наше значение, тем ниже правдоподобие модели, а нам нужно наоборот. К счастью, логарифмическое правдоподобие всегда отрицательно (так как обычное значение правдоподобия всегда меньше единицы), так что мы может просто взять противоположное значение.

Вот все это в виде одной функции:

def neg_log_likelihood(y,X,w):
    y_prob = logistic(jnp.dot(X,w))
    p_d_h = jnp.where(y == 1, y_prob, 1-y_prob)
    ll = jnp.sum(jnp.log(p_d_h))
    return -ll

Теперь мы можем посчитать отрицательное логарифмическое правдоподобие имеющихся данных для наших весов, еще до начала какого-либо обучения:

neg_log_likelihood(y_train,X_train,w)
> DeviceArray(619300.56, dtype=float32)

Как видно, отрицательное правдоподобие - это положительное число (ведь логарифм числа между 0 и 1 отрицателен). Теперь нам нужно найти такие значения весов w, которые уменьшают это значение, а значит увеличивают вероятность получения из весов известных нам данных.

Оптимизация - старый добрый градиентный спуск

Машина уже почти готова обучаться! Полезно думать о весах w, как определенной модели. С помощью отрицательного логарифмического правдоподобия мы можем различать, какая модель лучше или хуже - а именно, когда это значение ниже.

Мы имеем классическую оптимизационную задачу: необходимо последовательно понижать значение отрицательного правдоподобия до тех пор, пока мы не найдем значение, которое покажется нам самым низким. Мы будем использовать метод градиентного спуска - алгоритм нахождения минимума функции при помощи производной.

Так что осталось найти производную функции отрицательного логарифмического правдоподобия. Раньше нахождение градиента было трудной задачей, так как приходилось все производные считать руками. JAX делает эту процедуру тривиальной:

from jax import grad
d_nll_wrt_w = grad(neg_log_likelihood,argnums=2)

В этом коде мы получаем производную функции neg_log_likelihood по второму аргументу (нумерация начинается с нуля), то есть по весам w.

Далее мы создадим простую версию алгоритма градиентного спуска. Учитывая долгую популярностей нейронных сетей, существует большое количество учебников, разъясняющих детали этого метода, так что не будем в них вдаваться. Общая идея в том, что при помощи производной можно спускаться по значению функции до тех пор, пока мы не окажемся в локальном минимуме.

Добавим еще один шаг для более эффективного вычисления градиента:

from jax import jit
d_nll_wrt_w_c = jit(d_nll_wrt_w)

Так как наша реализация обучения весьма схематичная, можно просто повторить градиентный спуск несколько раз до тех пор, пока получаемые значения не сойдутся к чему-нибудь.

lr = 0.00001
for _ in range(1,200):
    w -= lr*d_nll_wrt_w_c(y_train,X_train,w)
print(neg_log_likelihood(y_train,X_train,w))
> 251421.27

Вот теперь мы обучили модель! Теперь надо посмотреть, насколько точно она описывает известные данные о пользовательских откликах на вакансии.

Статистика: “Но ведь это всего лишь…”

Хочу сделать небольшое отступление, чтобы обратиться к одному весьма распространенному среди специалистов по статистике заблуждению. Статистики сразу же распознают, что наша реализация персептрона полностью эквивалента логистической регрессии (подробнее об этом во второй части). Распространенное возражение со стороны статистики звучит так:

“Разве это и есть машинное обучение? Это же просто логистическая регрессия, которую мы применяем уже давно, не особо задумываясь обо все этом!”

Я поспорю, что важное отличие подхода машинного обучения в том, что мы действительно задумываемся обо все этом. О процессе оптимизации, о выборе функции потерь, о выборе метода оптимизации - все это неотъемлемая часть процесса моделирования. Например, для обычной линейной регрессии статистики наверняка прибегнут к методу наименьших квадратов. Это аналогично выбору среднеквадратической ошибка в качестве функции потерь, а это этого зависит, что мы можем делать при помощи нашей модели.

При увеличении сложности моделей вопросы о целевой функции и методах оптимизации выходят на первый план. Но даже в таком простом примере как наш функция отрицательного логарифмического правдоподобия была выбрана неслучайно, хотя существует множество способов обучиться практически тем же весам w. В следующих частях эта целевая функция позволит нам расширять модель с минимальным изменением кода.

Мы видим, что сама статистика трансформируется в этом направлении. Почти все работы в передовой области байесовского вывода требуют глубокого понимания алгоритмов оптимизации и численных методов. Другими словами, этот фокус на вычислимости и оптимизации и отличает машинное обучение от статистики.

Измерение эффективности модели машинного обучения

Сейчас полезно остановиться и подумать, что именно мы хотим измерять при оценке эффективности нашей модели. Конечная цель систем машинного обучения - предсказание какой-либо величины. Сейчас она выдает число от нуля до единицы, которые и составляет предсказание модели.

Эта модель также является классификатором. Мы представляем, что модель предсказывает, откликнется ли пользователь на данное объявление или нет. При построении классификатора мы добавим последнее преобразование, которое и будет решать, выдать 1 или 0 в качестве конечного результата.

Существует множество метрик эффективности моделей. Когда мы имеем дело с классификацией, естественно воспользоваться метрикой точности - отношением правильно сделанных предсказаний к их общему количеству. Но с этим методом есть две сложности. Первая становится очевидной, если мы подсчитаем долю откликов к общему количеству просмотров:

sum(y_train)/y_train.shape[0]
> 0.0899083179974852

Так что у нас здесь присутствует классическая проблема несбалансированных классов (хотя, мне кажется это странным отношением к ситуации, особенно учитывая, что мы моделируем долю отклика). Проблема в том, что просто предсказывая 0 для всех случаев даст весьма неплохую оценку точности.

Другая, менее явная проблема связана с тем, что мы по-настоящему еще не задумывались о том, как выбирать ответ 0 или 1. Почти во всех библиотеках алгоритмов машинного обучения порог выбора задан неявно как 0,5. И это почти всегда настраивается, но я встречал немало озадаченных взглядов от аналитиков после вопроса “какое пороговое значение используется в вашей модели?”. Более формально этот параметр задается минимальным softmax слоем нейронной сети.

Но мы обычно не знаем заранее, какое значение порога даст нам наилучшие предсказания пользовательских откликов, так что мы используем специальную метрику, показывающую, насколько хорошо работает одна и та же модель при разных значениях порога - ROC AUC (эта метрика заслуживает специального обсуждения в отдельной статье).

Если вы с ней незнакомы, ROC AUC вычисляет площадь под графиком функции соотношения истинноположительных и ложноположительных долей предсказаний при различных значениях порога. Обычно, ROC AUC 0,5 означает, что наш классификатор все равно, что угадывает результат, а значение 1,0 свидетельствует об идеальной классификации.

Давайте посмотрим на вычисление метрик обучающих и тестовых данных:

from sklearn import metrics
pred_train = logistic(np.dot(X_train,w))
fpr, tpr, thresholds = metrics.roc_curve(y_train, pred_train)
metrics.auc(fpr, tpr)
> 0.5758443732443408
pred_test = logistic(np.dot(X_test,w))
fpr, tpr, thresholds = metrics.roc_curve(y_test, pred_test)
metrics.auc(fpr, tpr)
> 0.5751280457175497

Получилось не хорошо. Такое значение говорит о том, что наш классификатор не может эффективно разделить пользователей, которые откликаются на вакансии от остальных. Может показаться, что наша модель провалилась.

Ограничения машинного обучения

Но действительно, так ли она плоха? Давайте для начала посмотрим, как мы обучились. Конечное правдоподобие было -251,422, а в начале - -619,300. Помним, что

\[\frac{A}{B} = e^{log(A) - log(B)}\]

Это значит, что мы улучшили изначальное правдоподобие вот во сколько раз:

\[e^{366878}\]

После обучения наша модель описывает данные лучше настолько, что мы даже не можем выразить коэффициент улучшения на компьютере! Так что мы многому научились.

Действительная проблема в том, как мы судим нашу модель. Точность, AUC, полнота, F1 - это все распространенные метрики для классификаторов. А мы в самом начале говорили о моделировании доли. Для моделирования долей и распределений всегда использовалась статистика.

Интерпретация задач моделирования распределений как задачи классификации - это одна из самых распространенных ошибок, которые я видел в машинном обучении. Сверхчеловеческая, идеальная модель распределения зачастую будет плохим классификатором.

Прекрасный пример этого - подбрасывание монеты. Если монета честная, и наша модель предсказывает вероятность выпадения орла ровно 0,5 без каких-либо неопределенностей, у нас есть идеальная модель поведения монеты. Но она же будет показывать ужасные результаты, если ее рассматривать как классификатор. Аналогично, представьте себе лотерею с шансом выигрыша в 1 / 1 000 000. Если ваша модель показывает точно и определенно шанс в 1 / 1 000 000, у вас прекрасная модель распределения. Но она будет отвратительным классификатором.

Даже если модели не работают как классификаторы, они могут дать нам ценную информацию для принятия решения в условиях неопределенности. Без правильной модели монеты мы можем принять неправильное решение о том, стоит ли ставить один доллар на монету, если при выпадении орла мы получим 2,1 доллара.

Проблема предсказания

Но проблема лежит глубже простого непонимания разницы моделирования распределения и классификации. Ведь мы можем рассматривать результат работы модели еще до применения порога принятия решения. Мы могли бы придумать какую-нибудь метрику, точнее измеряющую результат работы модели.

Но даже с этими изменениями, в конечном итоге модель дает нам всего лишь одно предсказание, точечную оценку отклика при имеющейся у нас информации. Любой сведущий человек сразу же спросит: “Насколько мы уверены в этой оценке?” Этот вопрос особенно актуален, если мы занимаемся чем-то вроде оптимизации рекламных аукционов или выплат премий за неопределенный риск. На такой вопрос отвечает статистический вывод.

Но обращаясь к выводу, нам придется обратить более пристальное внимание на то, чему именно обучилась наша модель. Это важно, так как распределения не существует в данных априорно - это часть нашей модели. Для понимания задач распределения необходимо понимать саму модель, а не только ее результаты.

Для этого нам нужен статистический вывод.